标签:不用 取值 是什么 窗口 方差 次方 观测 oat style
为什么要平稳?
研究时间序列的最终目的是,预测未来。但是未来是不可知的,我们拥有的数据都是历史,因此只能用历史数据来预测未来。但是,如果过去的数据与未来的数据没有某种“相似度”,那这种预测就毫无道理了。平稳性就是保证这种过去与未来的相似性,如果数据是平稳的,那么可以认为过去的数据表现出的某些性质,未来也会表现。
什么是严平稳?
对于一个时间序列{Xt},其中每个数据X都是随机变量,都有其的分布(如图)。
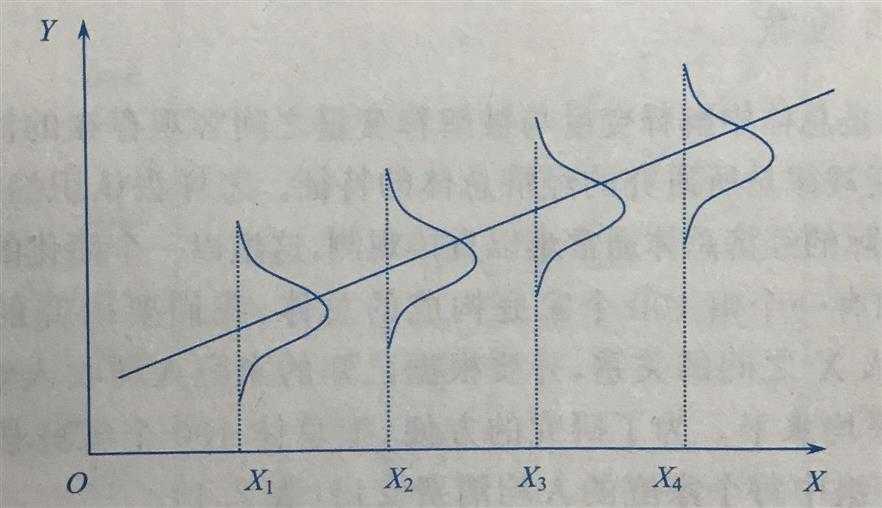
取其中连续的m个数据,X1到Xm,则可以构成一个m维的随机向量,(X1,X2,...,Xm)
由于单独的每个随机变量X都有各自的分布,那么组合成一个m维随机向量后,这个多维向量整体就有一个“联合分布”。
严平稳的本质就是,这种联合分布不随着时间的推移而变化。
也就是说,取数据时,任意连续取出的m个数据(无论是从X1取到Xm,还是从Xt取到Xt+m),他们组成的多维向量的联合分布都是相同的。
此时,再放宽一个条件,让这个m的取值也任意。
即无论这取数据的窗口设定为多宽,只要连续取相同数目个数据,他们构成的联合分布都是相同的。
比如,(X1,X2,X3)与(X6,X7,X8)有相同的3维联合分布,(X1,X2,X3,X4)与(X6,X7,X8,X9)有相同的4维联合分布。
综上,符合上述性质的时间序列,是严平稳的。
有了严平稳为什么还要有宽平稳?
很多情况下,我们无从得知这些随机变量的分布到底是什么样子。
我们观测得到的数据,只是服从某种未知分布的随机变量的一种取值。
既然连单个随机变量的分布都难以求出,就更不用说求由一堆随机变量组成、多维随机向量的联合分布有多困难了。
因此严平稳虽然是一种保证过去与未来的数据“相似”很棒的方式,但过于理想化,实际上很难检验一个时间序列的严平稳性。
于是只能放宽条件,因而产生了“宽平稳”的概念。
什么是“k阶矩”?
“矩”是随机分布的一种特征数。特征数,顾名思义,反映了一个随机分布的某种特征。比如“数学期望”反映了,符合某种分布的随机变量的取值,总是在某个值周围波动;而“方差”则反映了,这种波动的大小程度。
矩分为原点矩和中心矩,其中一阶原点矩就是数学期望,二阶中心矩就是方差。
但是这两者之间有相互推导的公式,知其一就可推其二,因此一般只称为矩。
其中,随机变量的k阶原点矩的定义为,随机变量的k次方的数学期望,即E(Xk)。平时所说的“k阶矩存在”,就表现为这个数学期望不是无穷(也就是小于无穷),这与“极限存在”的定义是同理的。
值得注意的是,如果一个随机变量的某高阶矩存在,那么比起阶数更低的矩也一定存在。因为|X|k-1≤|X|k+1。
严平稳中由于联合分布相同,故各阶矩也相同。
什么是宽平稳?
当时间序列满足三个条件时,就被称为是宽平稳的。
第一个条件是,任意时刻二阶矩都存在。
标签:不用 取值 是什么 窗口 方差 次方 观测 oat style
原文地址:https://www.cnblogs.com/ev2020/p/12344803.html