标签：array   多次   二分查找   ima   维护   增加   符号   通过   时间   

B+树作为索引最为常见，亦是数据库中最为频繁的一种索引。

B+树通过二叉查找树，再由平衡二叉树，最后加B树演化而来。

1. 二分查找法

二分查找法（binary search）也叫折半查找法，从有序数组中查询某一条记录。

基本思想：将记录按有序（递增或递减）排列，先查找数组中的中间位置的对象，如果target < array[mid]，那么就去左半边；如果target > array[mid]，就去右半边。因此时间只需要O(logn)。

2. 二叉查找树

 在二叉查找树中，左子树节点的值总是小于根节点的值，右子树节点的值总是大于根节点的值。因此使用中序遍历的话，就是一个递增的有序序列。

缺点：构建二叉查找树的时候，可能搞成一棵效率低下的二叉树，即二叉树的高度为数组的长度。用数组第一个数或是最后一个数作为根节点的时候。此时查找效率上和顺序查找是一样的。

3. 平衡二叉树

由于二叉查找树的缺陷，那么就将二叉查找树弄成一棵平衡树——平衡二叉树（AVL树，G. M. Adelson-Velsky和E. M. Landis 发明的）。

定义：1）符合二叉查找树的特点，左子树 < 根 < 右子树；2）满足任何节点的两个子树的高度最大差为1。

虽然平衡二叉树的查询效率很高，但是维护的代价也不小，当插入、删除、更新的时候需要一次或是多次左旋或右旋操作。

如下图：

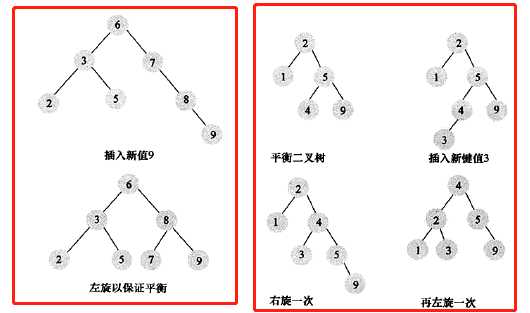
 左边是插入9的知识后只要一次左旋操作就可以，右边插入3的时候则需要两次旋转操作。

4. B树（B-Tree，不是B减树，就读作B树，中间就一个连字符号）

B树属于多叉树又名平衡多路查找树（不止是二叉）。

定义：

1. 排序方式：所有节点关键字的值是按照递增排列，左小右大；
2. 子节点数：1 < 非叶子节点的子节点数 <= M，M >= 2，空树除外。M代表一棵树节点最多有多少个查找路径，M=M路，当M=2时则是2叉树，M=3时则是3叉，M也是B树的阶，常说m阶B树。
3. 关键字数：ceil(M/2) - 1 <= 关键字数j <= m-1，ceil为数轴正部分取证(ceil(1.01) = 2）；
4. 所有叶子结点在同一层，叶子结点除了包含关键字和关键字记录的指针外还有指向其子节点的指针，只不过叶子节点指向子节点的指针都指向null

一棵B树如下图所示：

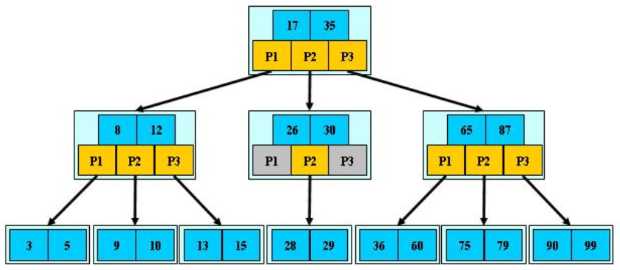
 依旧有二叉查找树和平衡二叉树的性质：左孩子节点的值 < 根节点的值 < 右孩子节点的值

5. B+树

B+树是B树的一个升级。

定义：

1. 不同于B树，B+树的非叶子节点不再保存关键字记录的指针，只进行数据索引，使得B+树每个非叶子节点所能保存的关键字增加；
2. B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取，所以每次查询效率一样；
3. 所有叶子结点都有一个指向右边叶子节点的指针；
4. 所有数据都保存在叶子结点。

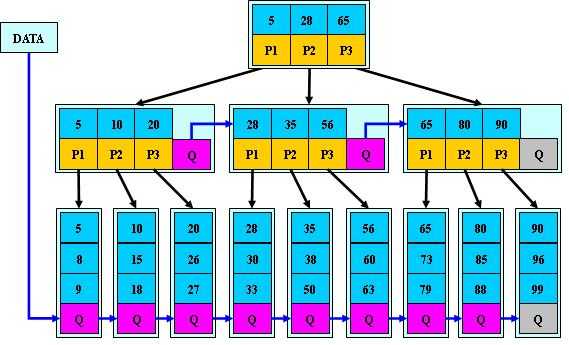
一棵B+树如下图所示：

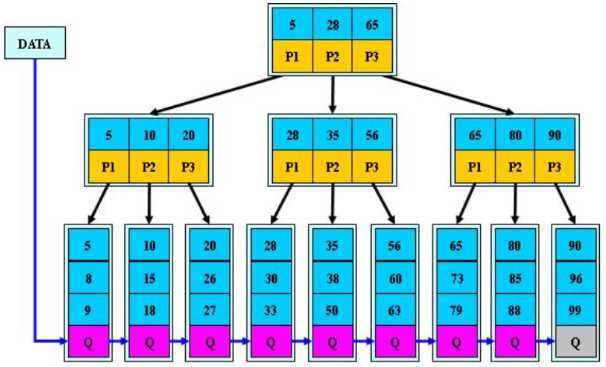
 有一个B+树：5,10,15,20,25,30,50,55,60,65,75,80,85,90。

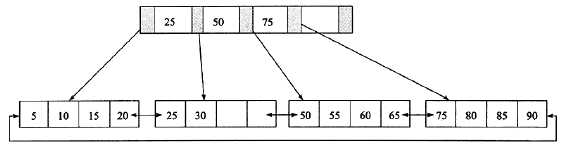
 插入操作：

1. 叶子结点和非叶子节点都没有满的时候，直接将记录插入到叶子节点。

插入28

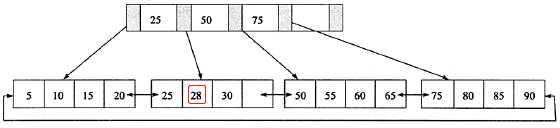
 2. 叶子结点满了，非叶子节点没有满

1. 拆分叶子节点
2. 将中间的节点放入父节点中
3. 小于中间节点的值放入左边
4. 大于或等于中间的值放入右边

接上次插入28之后，插入70

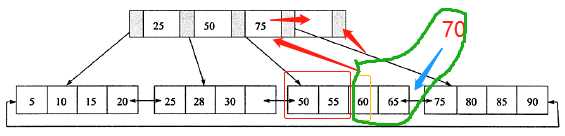
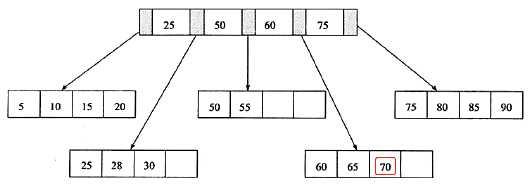
 3. 叶子结点满了，父节点（非叶子节点）也满了

1. 拆分叶子结点
2. 小于中间节点的值放左边
3. 大于或等于中间节点值的放右边
4. 拆分父节点
5. 小于中间节点的放左边
6. 大于中间节点的放右边（等于中间的节点应该也要加上吧，不然索引就不全了吧）
7. 中间节点放入上一层非叶子节点（该节点的父节点）

接上次插入70后再插入95

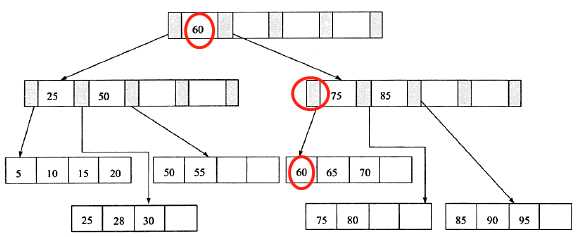
 感觉空着的那个红圈那里是否应该将60写上？个人觉得应该是要写上。。。。

 如果有幸您路过看到的话，希望您可以给我一点点思路，这种纠结着的话有点点难受。。。插入图片内容来自MySQL技术内幕B+树部分。。。

 B*树简单来说就是把非叶子节点也连接起来。。。。。。。。。。

B+树

标签：array   多次   二分查找   ima   维护   增加   符号   通过   时间   

原文地址：https://www.cnblogs.com/baishouzu/p/12346229.html