标签:str 情况 syn pre 任务 style cst com mem
题目意思:有个3*n的扫雷游戏,其中中间那行是没有雷而且格子是全部点开的,给出中间那行的数字,根据这串数字统计两边有几种埋雷方案
样例输入:
2
22
000
样例输出:
6
1
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=5965
对于这个埋雷问题,我们首先注意到的是某个雷如果被埋下了,那么这个雷的信息会被它周围的三个格子所共享,但是对三个格子之外的格子就没什么影响了
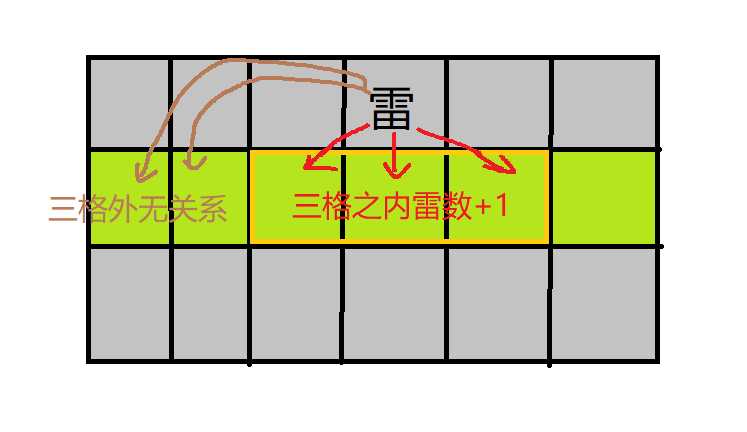
反过来我们也能想到,对于中间那行某个格子内的数字,也只是影响到它上下三格以内的雷的摆放
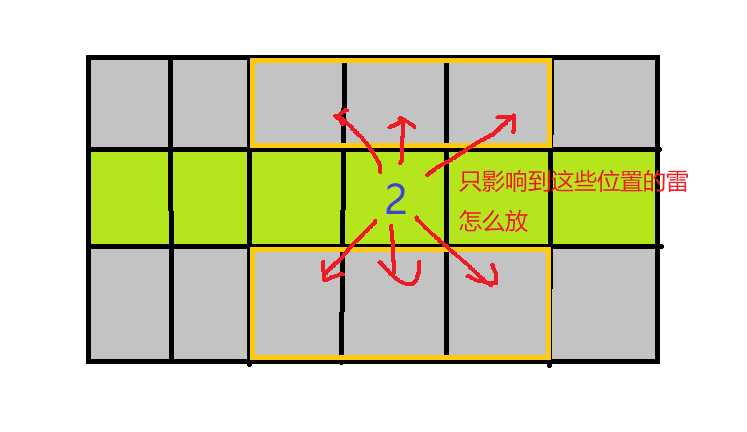
这里就会给我们一个dp的启发,就是对于中间的第i个格子来说,摆到这个格子的方案数应该能由前面格子的已知摆放方案数推出来,并且这个递推是乘法关系的递推,就是摆到那个格子的方案数应该等于它之前格子摆的方案数乘上它现在这个格子提示数字所能摆的方案数。
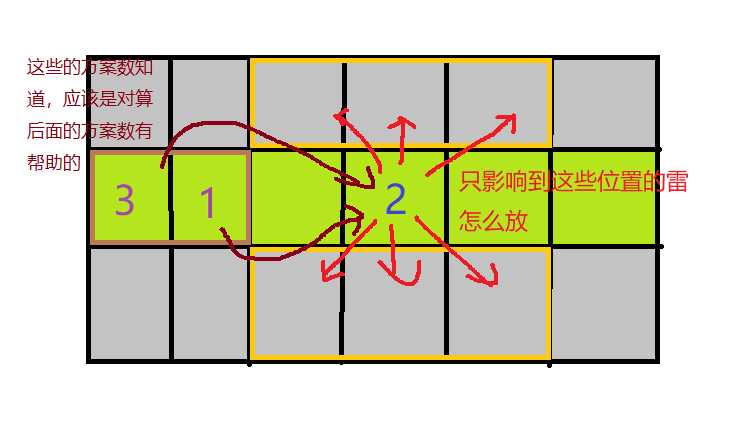
对于dp的模型,我们有个直观的想法就是用f[i]表示摆到第i个格子的方案数,这样f[n]就是我们需要的答案,然后开始想状态转移方程

但是我们发现,尽管三格之外的的信息能直接作为方案数的乘法推算的一部分,但是由于三格之内的数字所提示的埋雷信息是共享的,导致一个单纯的f[i]推到这里就推不动了,因为i所能提示的信息只有第几个格子,不涉及具体的摆雷信息,所以只用一个i就把正确的状态转移方程得出来是不可能的。既然这样,我们就得考虑增加状态信息,并且这些信息要涉及埋雷方法,所以我们的任务就变成了怎么去合理得设计状态,使得这些状态能把埋雷情况表示出来。
这里的设计方案是是增加三个信息a, b, c,分别表示埋到第i个数字,然后这个数字的左边放了a个雷,中间放了b个雷,右边放了c个雷
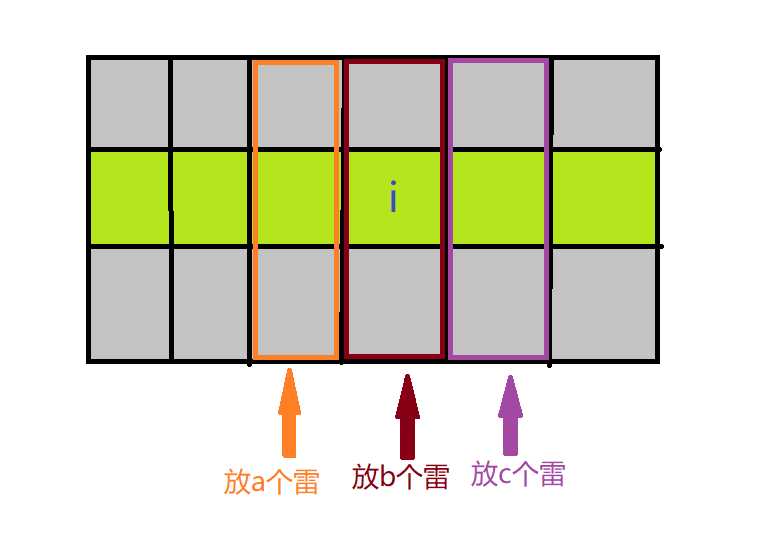
那么数组就变成了f[i][a][b][c],设第i个数字为num[i],我们所需的答案就是f[n][a][b][0],其中a + b = num[i],就是对于最后一个数字我们不能再往它右边摆雷
这样子设计有什么好处呢?如果第i个数字的左边放了a个雷,中间放了b个雷,对于第i-1个数字来说就是中间放了a个雷,右边放了b个雷,就是对于f[i]跟f[i-1]来说,由于a跟b的两个信息的共享,f[i]跟f[i-1]的关系变得清晰了,那么我们就很容易推知f[i][a][b][c] = f[i-1][num[i-1] - a - b][a][b] * (数字i的右边摆c颗雷的方案数),其中a+b+c = num[i],意思是对于第i个数字来说,它周围的雷就必须是这么多,而num[i-1] - a - b的意思是既然第i-1个数字的右边跟中间分别放了a颗雷跟b颗雷,那么它的左边就只能放num[i-1] - a - b颗雷了,需要注意的是这个数可能会是负数也有可能大过2,这种情况说明了不存在这种abc摆雷方案,让整个式子等于0即可,而数字i右边摆c颗雷的方案数,我们知道这个c只能等于0,1, 2,那么我们就可以预处理个solution[3]数组把这些相应的摆雷方案数存下来即可。
至于初始状态,这个也好弄,就是第一个数字,我们不能往左边格子放雷,也就是a = 0,b+c = num[1]的情况,f[1]单独拿出来算一次我们就能得到初始状态了。
所以这里的整个状态方程就是
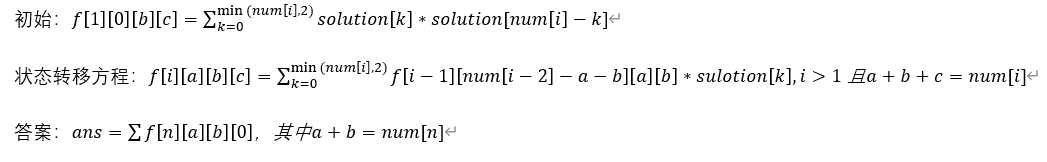
直接看公式我自己都觉得头大,大家看看上边的分析自己看着写即可
贴上AC代码:
#include<iostream> #include<cstring> #include<string> #define _rep(i, l, r) for(int i=l; i<=r ;i++) using namespace std; const int Maxn = 1e4 + 10; const int M = 100000007; int num[Maxn]; int f[Maxn][3][3][3]; int solution[3] = { 1, 2, 1 }; void Ini() { memset(num, 0, sizeof(num)); memset(f, 0, sizeof(f)); } void Input(string& str) { cin >> str; for (int i = 0; i < str.size(); i++) { num[i+1] = str[i] - ‘0‘; } } void solve(int n) { _rep(b, 0, 2) _rep(c, 0, 2) { if (b + c != num[1]) continue; f[1][0][b][c] = solution[b] * solution[c]; } for (int i = 2; i <= n; i++) { _rep(a, 0, 2) _rep(b, 0, 2) _rep(c, 0, 2) { if (a + b + c != num[i]) continue; int res = num[i - 1] - a - b; if (res < 0 || res > 2) continue; f[i][a][b][c] = (f[i][a][b][c] + solution[c] * f[i - 1][res][a][b]) % M; } } int ans = 0; _rep(a, 0, 2) _rep(b, 0, 2) { if (a + b != num[n]) continue; ans = (ans + f[n][a][b][0]) % M; } cout << ans << endl; } int main() { ios::sync_with_stdio(false); int T; cin >> T; while (T--){ string str; Ini(); Input(str); int n = str.size(); solve(n); } return 0; }
标签:str 情况 syn pre 任务 style cst com mem
原文地址:https://www.cnblogs.com/wulichenai/p/12346766.html