标签:二分 xpl 就会 test png 扫描 为我 竖线 log
前置知识:线段树
扫描线主要是一种思想,利用线段树来解决矩形的面积/周长问题
以求多个矩形面积并为例

如图我们现在需要求二维平面上这三个矩形的面积并,也就是涂色的面积,各矩形的边相互平行,矩形的位置坐标都是已知的
像这样堆叠起来的的图形并没有直接的面积公式可以用,如果要用原始数据硬算的话,就是分别计算出每个矩形的面积加起来,然后再减去重复计算的部分,有的部位还可能会被重复计算多次,总之是相当麻烦,而且显然这样计算并不好用代码来实现
那么我们换个思路
在每个矩形的两条水平边处都引出一条直线(竖直边也可以,此处以水平边为例)
这样n个矩形就会出现最多2n条平行线(因为可能会有重合的直线,所以数量可能会小于2n)
这些直线会把整个图形分割成若干个区域,显然每个区域中的涂色部分都是矩形,这样就可以直接长乘宽直接计算每个色块的面积,然后全都加起来得到答案,而且这样计算也不会出现重复的情况
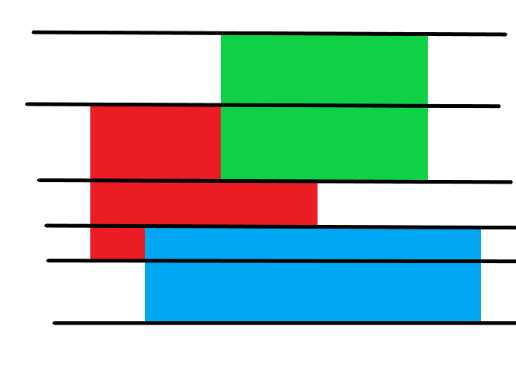
扫描线的计算思路就是这样,接下来我们就来看一下如何实现
想要这样计算需要知道每个划分区域的涂色部分的长和宽(假设水平的边是长,竖直边是宽)
首先我们用结构体保存题目给出的每个矩形的上下边的信息,记录下它们的左右端点和高,即每个线段左右端点的x坐标和这条线段的y坐标,并且记录这条边是上边还是下边,然后按照高将这2n条边从小到大排序
struct node
{
int l,r,h; //这条边左右端点的x坐标,和这条边的y左边
int type; //type==1表示这条边是下边,-1表示上边
}edge[maxn];排序之后相邻两个线段的高度之差就可以表示这两个线段所在分割线之间的色块的宽,如果这两个相邻线段的高相等的话我们可以认为存在一个宽为0的色块,计算出面积为0,不影响结果
这样我们从 i=1 遍历到 i=n-1 ,拿宽 (edge[i+1].h-edge[i].h) 乘以长就可以了
但是涂色部分的长并不能直接减出来,因为我们并不能确定色块的长的范围是从哪到哪,更何况有可能某一划分区域中是不连续的多段色块,比如
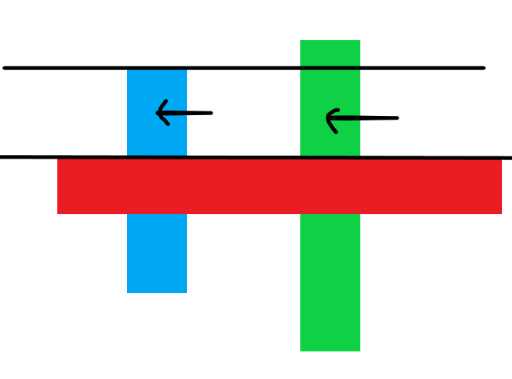
不过我们可以用线段树
edge[i] 从 i=1 遍历到 i=n-1 就像一条线从下往上扫描整个图形一样,
如果扫过了一个矩形的下边,那么接下来的区域中的涂色部分的范围肯定是包含这条下边的
如果扫过了一个矩形的上边,那么接下来的区域中的涂色部分的范围可能不包含这条上边,因为可能还会被其他矩形覆盖
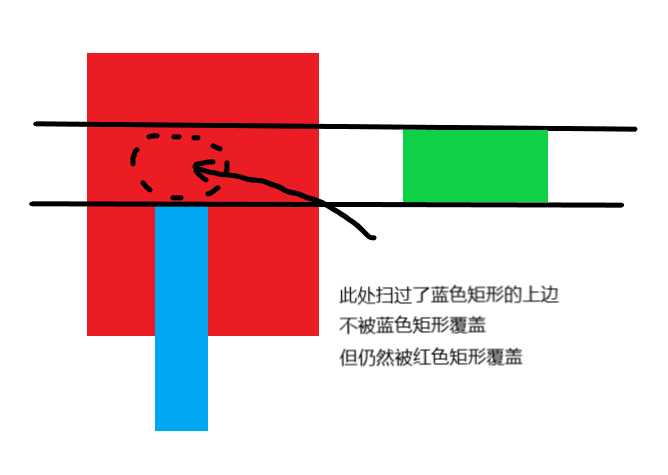
利用线段树来维护这条线上的区间覆盖情况,当前边是下边的话就让对应区间的覆盖次数+1,扫到上边的话就-1
每当需要计算长的时候直接线段树查询被覆盖的区间长度之和就可以了
最后计算的面积总和就是答案
ps:有很多题目的坐标范围很大或者是浮点型数据,就需要离散化一下了
上代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
struct node
{
double l,r,h;
int type;
}edge[210];
double pos[210]; //离散化数组,记录横坐标
int cover[400010];
double len[400010]; //用数组建线段树,cover[]表示此区间被覆盖次数。len[]表示此区间被覆盖长度
void init()
{
memset(cover,0,sizeof(cover));
memset(len,0,sizeof(len));
}
bool cmp(node a,node b)
{
return a.h<b.h;
}
int func(int l,int r,double x)
{
while(l<=r)
{
int mid=(l+r)/2;
if(pos[mid]==x) return mid;
if(x<pos[mid]) r=mid-1;
else l=mid+1;
}
}
void pushup(int tl,int tr,int id)
{
if(cover[id]) len[id]=pos[tr]-pos[tl]; //如果cover[i]大于0表示这个区间被覆盖过,len[i]直接等于区间长度,
else if(tl+1==tr) len[id]=0; //cover[i]等于0相当于没被完全覆盖,但也有可能局部被覆盖了,
else len[id]=len[id*2]+len[id*2+1]; //所以len[i]等于两个儿子的len之和
}
void updata(int tl,int tr,int id,int l,int r,int val)
{
if(l<=tl&&tr<=r)
{
cover[id]+=val;
pushup(tl,tr,id); //cover[]和len[]的信息不需要向上传也不需要向下传,只要表示当前节点的状态就好,
return ; //这样每次查询就应该是O(logn)的复杂度(大概叭O.o
}
int mid=(tl+tr)/2;
if(l<mid) updata(tl,mid,id*2,l,r,val);
if(mid<r) updata(mid,tr,id*2+1,l,r,val);
pushup(tl,tr,id);
}
int main()
{
int n,cas=0;
while(~scanf("%d",&n))
{
if(!n) break;
init();
double x1,y1,x2,y2;
for(int i=0;i<n;i++)
{
scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2); //输入矩形信息
edge[i*2]={x1,x2,y1,1};
edge[i*2+1]={x1,x2,y2,-1};
pos[i*2]=x1;
pos[i*2+1]=x2;
}
sort(pos,pos+2*n);
int top=0;
for(int i=1;i<2*n;i++) if(pos[i]!=pos[i-1]) //pos数组去重,离散化横坐标
pos[++top]=pos[i];
sort(edge,edge+2*n,cmp); //边按高度从小到大排序
double ans=0;
for(int i=0;i<2*n-1;i++) //遍历排好序的每一条边,相当于自下向上扫描
{
int l=func(0,top,edge[i].l); //二分查找这条线段的端点在离散化数组中的下标
int r=func(0,top,edge[i].r);
updata(0,100000,1,l,r,edge[i].type); //更新线段树
ans+=(edge[i+1].h-edge[i].h)*len[1]; //长乘宽计算面积
}
printf("Test case #%d\n",++cas);
printf("Total explored area: %.2f\n\n",ans);
}
return 0;
}求周长有两种方法,上面求面积并的时候可以看到我们能利用线段树求出总区间的覆盖长度,但是这个长度不能直接加在周长上,因为可能会出现重复计算的情况
所以,扫当前边时的覆盖长度,和扫过上一条边时的覆盖长度,它们的变化量,即这本次扫描的 len[1] 和上一次扫描的 len[1] 之差的绝对值,就是当我们扫到当前这条边时新增的周长
但是有一点千万千万要注意,就是给边排序的时候不能单纯的按高度大小来排了,如果有高度相同的边,要把下边放在上边的前面,保证先加覆盖次数,再减覆盖次数
这里可以手动模拟一下,比如一上一下两个矩形共用一条边这种情况,如果把下面矩形的上边排在上面矩形的下边前边的话就会出现重复计算的情况
像这样从下到上扫过一遍后就可以求出水平边的周长,我们只需要在左右方向再做一遍扫描线求出竖直线的周长,将他们加起来就可以了
这就是两遍扫描线求周长的方法,还有一种只需要扫一遍的方法
实际上可以发现只要把每个划分区域中的竖线长度,也就是两条分割线的间距,都加起来,竖线的周长就出来了,再加上用扫描线求得的水平线长度,扫一遍周长就解决了
唯一需要解决的问题就是每个划分区域中有几个色块,色块数量的2倍就是竖线个数
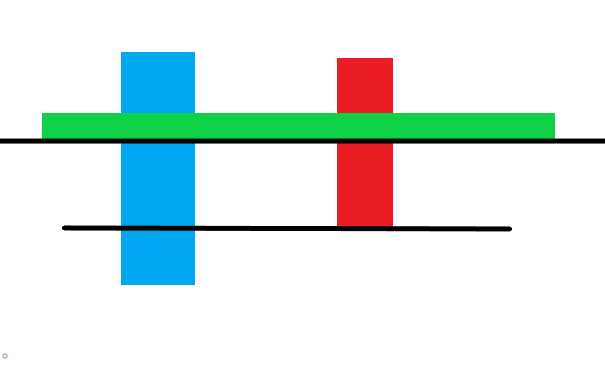
如图两条分割线之间就有2个色块,4条竖线
那么我们就需要线段树多维护一个信息,见代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
struct node
{
int l,r,h,type;
}edge[10010];
int cover[40010],len[40010];
int lc[40010],rc[40010],num[40010]; //依然用数组建树,但是线段树维护的内容多了lc,rc,num
int pos[10010]; //lc表示当前区间的左端点是否被覆盖,rc表示右端点是否被覆盖,num表示当前区间色块数量
void init()
{
memset(cover,0,sizeof(cover));
memset(len,0,sizeof(len));
memset(lc,0,sizeof(lc));
memset(rc,0,sizeof(rc));
memset(num,0,sizeof(num));
}
bool cmp(node a,node b)
{
return a.h==b.h?a.type>b.type:a.h<b.h; //注意排序方式有些变化,有多个高度相同的边时要保证下边排在上边的前面
}
int func(int l,int r,int x)
{
while(l<=r)
{
int mid=(l+r)/2;
if(x==pos[mid]) return mid;
if(x<pos[mid]) r=mid-1;
else l=mid+1;
}
}
void pushup(int tl,int tr,int id)
{
if(cover[id])
{
len[id]=pos[tr]-pos[tl]; //如果cover>0,表示当前区间被完全覆盖
lc[id]=rc[id]=1; //左右端点都被覆盖,色块数量为1,即lc=rc=num=1
num[id]=1;
}
else if(tl+1==tr)
{
len[id]=0; //叶子节点都是0
lc[id]=rc[id]=0;
num[id]=0;
}
else
{
len[id]=len[id*2]+len[id*2+1]; //cover==0的表示当前区间未被完全覆盖,但也有可能被局部覆盖,所以num等于俩儿子的num之和
lc[id]=lc[id*2],rc[id]=rc[id*2+1]; //但是如果左儿子的右端点和右儿子的左端点同时被覆盖则表示左儿子最右面的色块和右儿子最左面的其实是一块,
num[id]=num[id*2]+num[id*2+1]-(rc[id*2]&&lc[id*2+1]); //这种情况下就需要num-1
}
}
void updata(int tl,int tr,int id,int l,int r,int val)
{
if(l<=tl&&tr<=r)
{
cover[id]+=val;
pushup(tl,tr,id);
return ;
}
int mid=(tl+tr)/2;
if(l<mid) updata(tl,mid,id*2,l,r,val);
if(mid<r) updata(mid,tr,id*2+1,l,r,val);
pushup(tl,tr,id);
}
int main()
{
int n;
while(~scanf("%d",&n))
{
init();
for(int i=0,x1,y1,x2,y2;i<n;i++)
{
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
edge[i*2]={x1,x2,y1,1};
edge[i*2+1]={x1,x2,y2,-1};
pos[i*2]=x1;
pos[i*2+1]=x2;
}
sort(pos,pos+2*n);
int top=0;
for(int i=1;i<2*n;i++) if(pos[i-1]!=pos[i])
pos[++top]=pos[i];
sort(edge,edge+2*n,cmp);
ll ans=0;
int lst=0;
for(int i=0;i<2*n;i++)
{
int l=func(0,top,edge[i].l);
int r=func(0,top,edge[i].r);
updata(0,top,1,l,r,edge[i].type);
ans+=abs(len[1]-lst); //lst为上次扫描的长度,与本次扫描长度之差的绝对值就是新增的水平长度
if(i<2*n-1) ans+=1LL*(edge[i+1].h-edge[i].h)*num[1]*2; //num[1]表示这个划分区域的色块数量,计算新增的竖直周长
lst=len[1];
}
printf("%lld\n",ans);
}
return 0;
}只需要在线段树维护的信息上改动一下,新增len2,用len1表示该区间中被覆盖一次的长度,len2表示覆盖两次的长度
这样在更新节点信息的时候cover>=2的直接len2等于区间长度
cover==1的表示该区间被完整覆盖过一次,但是局部可能覆盖两次以上,所以len2等于俩儿子的len1之和
cover==0就表示该区间没有被完全覆盖过,直接len2就等于俩儿子的len2之和
如果题目要求覆盖三次、四次…以上的就按这样来就行
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
struct node
{
double l,r,h;
int type;
}edge[2010];
double pos[2010];
double len1[8010],len2[8010];
int cover[8010];
void init()
{
memset(len1,0,sizeof(len1));
memset(len2,0,sizeof(len2));
memset(cover,0,sizeof(cover));
}
bool cmp(node a,node b)
{
return a.h<b.h;
}
int func(int l,int r,double x)
{
while(l<=r)
{
int mid=(l+r)/2;
if(x==pos[mid]) return mid;
if(x<pos[mid]) r=mid-1;
else l=mid+1;
}
}
void pushup(int tl,int tr,int id)
{
if(cover[id])
{
len1[id]=pos[tr]-pos[tl];
if(cover[id]>1) len2[id]=pos[tr]-pos[tl];
else
{
if(tl+1==tr) len2[id]=0;
else len2[id]=len1[id*2]+len1[id*2+1];
}
}
else if(tl+1==tr) len1[id]=len2[id]=0;
else
{
len1[id]=len1[id*2]+len1[id*2+1];
len2[id]=len2[id*2]+len2[id*2+1];
}
}
void updata(int tl,int tr,int id,int l,int r,int val)
{
if(l<=tl&&tr<=r)
{
cover[id]+=val;
pushup(tl,tr,id);
return ;
}
int mid=(tl+tr)/2;
if(l<mid) updata(tl,mid,id*2,l,r,val);
if(mid<r) updata(mid,tr,id*2+1,l,r,val);
pushup(tl,tr,id);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
init();
int n;
scanf("%d",&n);
double x1,x2,y1,y2;
for(int i=0;i<n;i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
edge[i*2]={x1,x2,y1,1};
edge[i*2+1]={x1,x2,y2,-1};
pos[i*2]=x1;
pos[i*2+1]=x2;
}
sort(pos,pos+2*n);
int top=0;
for(int i=1;i<2*n;i++) if(pos[i]!=pos[i-1])
pos[++top]=pos[i];
sort(edge,edge+2*n,cmp);
double ans=0;
for(int i=0;i<2*n;i++)
{
int l=func(0,top,edge[i].l);
int r=func(0,top,edge[i].r);
updata(0,top,1,l,r,edge[i].type);
ans+=(edge[i+1].h-edge[i].h)*len2[1];
}
printf("%.2f\n",ans);
}
return 0;
}本题要求的是被覆盖了三次以上的体积
因为z坐标的范围比较小才不到500,所以我们可以把矩形的上下平面按z坐标大小排序,遍历所有z坐标,跑多次扫描线
每遍扫描线求出平行于当前xoy平面上的相交三次的面积后,再乘以高度差z,就得到相邻两个xoy平面之间夹的体积了
需要注意的是,每次求扫描线时涉及到的边由立方体的下平面的z坐标小于等于当前枚举的z且立方体的上平面的z坐标大于当前枚举的z的立方体提供
。。。这句话有点长,断句为
每次求扫描线时涉及到的边由{[(立方体的下平面)的z坐标小于等于当前枚举的z]且[(立方体的上平面)的z坐标大于当前枚举的z]的立方体}提供
因为其他的立方体并不会对当前xoy平面产生贡献
然后更新线段树的规则和求面积交时类似,这次又多了个len3
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
struct node
{
int l,r,h,type;
}edge[2010];
struct save
{
int x,y,z;
}point[2010];
int posx[2010],posz[2010];
int cover[8010];
int len1[8010],len2[8010],len3[8010];
void init()
{
memset(cover,0,sizeof(cover));
memset(len1,0,sizeof(len1));
memset(len2,0,sizeof(len2));
memset(len3,0,sizeof(len3));
}
bool cmp(node a,node b)
{
return a.h<b.h;
}
int func(int l,int r,int x)
{
while(l<=r)
{
int mid=(l+r)/2;
if(x==posx[mid]) return mid;
if(x<posx[mid]) r=mid-1;
else l=mid+1;
}
}
void pushup(int tl,int tr,int id)
{
if(cover[id]) len1[id]=posx[tr]-posx[tl];
else if(tl+1==tr) len1[id]=0;
else len1[id]=len1[id*2]+len1[id*2+1];
if(cover[id]>1) len2[id]=posx[tr]-posx[tl];
else if(tl+1==tr) len2[id]=0;
else if(cover[id]==1) len2[id]=len1[id*2]+len1[id*2+1];
else len2[id]=len2[id*2]+len2[id*2+1];
if(cover[id]>2) len3[id]=posx[tr]-posx[tl];
else if(tl+1==tr) len3[id]=0;
else if(cover[id]==2) len3[id]=len1[id*2]+len1[id*2+1];
else if(cover[id]==1) len3[id]=len2[id*2]+len2[id*2+1];
else len3[id]=len3[id*2]+len3[id*2+1];
}
void updata(int tl,int tr,int id,int l,int r,int val)
{
if(l<=tl&&tr<=r)
{
cover[id]+=val;
pushup(tl,tr,id);
return ;
}
int mid=(tl+tr)/2;
if(l<mid) updata(tl,mid,id*2,l,r,val);
if(mid<r) updata(mid,tr,id*2+1,l,r,val);
pushup(tl,tr,id);
}
int main()
{
int T;
scanf("%d",&T);
for(int cas=1;cas<=T;cas++)
{
int n;
scanf("%d",&n);
for(int i=0,x1,y1,z1,x2,y2,z2;i<n;i++)
{
scanf("%d %d %d",&x1,&y1,&z1);
scanf("%d %d %d",&x2,&y2,&z2);
point[i*2]={x1,y1,z1};
point[i*2+1]={x2,y2,z2};
posx[i*2]=x1,posx[i*2+1]=x2;
posz[i*2]=z1,posz[i*2+1]=z2;
}
sort(posx,posx+2*n);
sort(posz,posz+2*n);
int topx=0,topz=0;
for(int i=1;i<2*n;i++) if(posx[i]!=posx[i-1]) posx[++topx]=posx[i];
for(int i=1;i<2*n;i++) if(posz[i]!=posz[i-1]) posz[++topz]=posz[i];
ll res=0;
for(int i=0;i<=topz;i++)
{
init();
int top=0;
for(int j=0;j<2*n;j+=2) if(point[j].z<=posz[i]&&point[j+1].z>posz[i])
{
edge[top++]={point[j].x,point[j+1].x,point[j].y,1};
edge[top++]={point[j].x,point[j+1].x,point[j+1].y,-1};
}
sort(edge,edge+top,cmp);
ll ans=0;
for(int j=0;j<top;j++)
{
int l=func(0,topx,edge[j].l);
int r=func(0,topx,edge[j].r);
updata(0,topx,1,l,r,edge[j].type);
ans+=1LL*len3[1]*(edge[j+1].h-edge[j].h);
}
res+=ans*(posz[i+1]-posz[i]);
}
printf("Case %d: %lld\n",cas,res);
}
return 0;
}标签:二分 xpl 就会 test png 扫描 为我 竖线 log
原文地址:https://www.cnblogs.com/JDZJBD/p/12348370.html