标签:使用 快速 ati 完全 width 种类 定义 一课 inf
树这种结构 本身在计算机科学领域 占有很重要的地位,这种数据结构之所以占有重要的地位,不仅仅是因为二分搜索树这样的一种结构, 是树本身这种形状可以产生很多拓展,对于不同的问题 ,我们可以稍微改变 或者 限制树这种数据结构的性质,从而产生不同的数据结构,高效的解决不同的问题,
从节开始,将会有四个章节介绍 四个不同的例子,它们分别是堆,线段树,字典树 以及 并查集 ,通过这些不同的树的结构,我们可以领会到 数据结构的灵活之处,
优先队列(相对 高层的数据结构) 是 出队,入队和 顺序 无关,和 优先级 有关,其实用的最多是 谁优先出队,
优先队列的接口 和 普通队列是一样,只不过是在出队操作上 和 队首 元素上 是不同的,

优先队列的底层结构 实现也是可以由不同数据结构来构成, 这里提供的是三种类型的数据结(普通线性结构 , 顺序线性结构, 堆)
这里假设 优先级 是谁最大 ,

这里是用堆作为数据结构 作为优先队列的底层实现, 如果有时间也可以用 普通线性结构 或者顺序线性结构 来实现 优先队列 然后 再和 我们这里用堆实现的 优先队列 去比较性能,这有助于 对数据结果的学习!
在计算机的世界中,凡是时间复杂度 为 logn 的,那么差不多一定 和树这个结构有关系, 归并排序 和 快速排序 它们都是logn 级别的,(虽然没有直接使用树,但是它的递归过程 其实是个隐形 树 )
一个堆本身,其实也是一颗树,
二叉堆 是一个特殊的树, 二叉堆 是一课完全二叉树,
满二叉树: 除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
完全二叉树:完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
满二叉树:
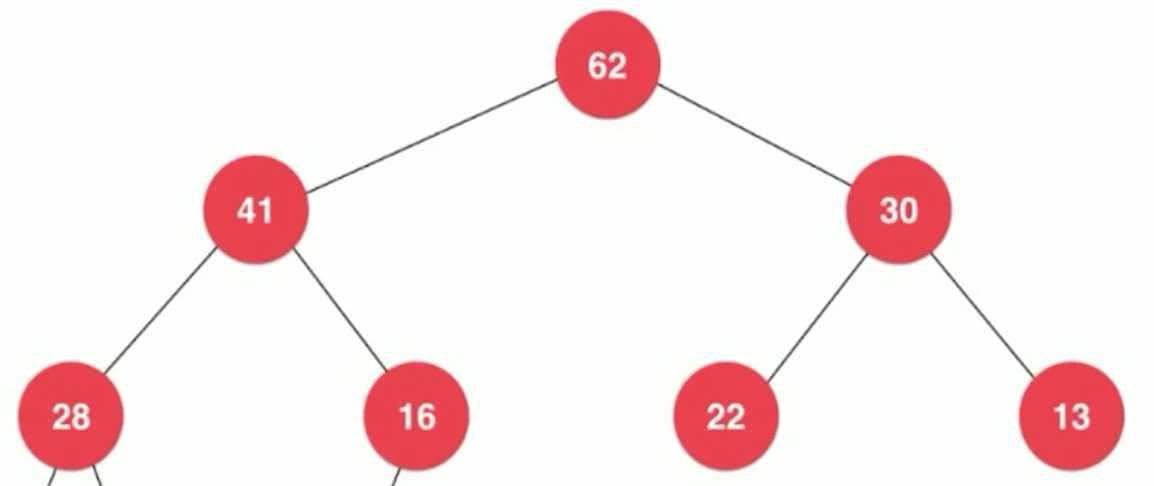
完全二叉树: (其实就是一层一层的放,直到放不下了 )
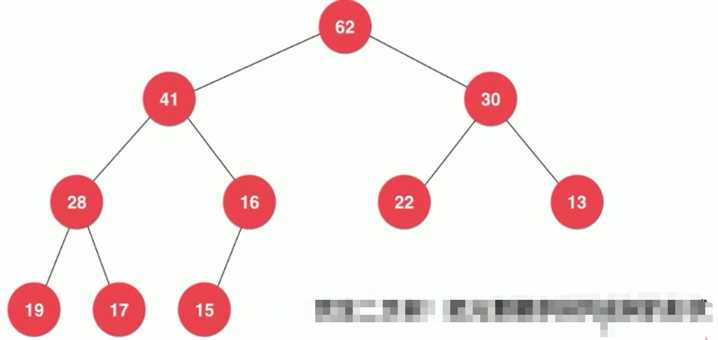
二叉堆 首先是个完全二叉树,除此之外,
它还有个特殊的性质: 堆中 每个节点的值总是 不大于 其父节点的值 (所有个节点值都大于它的孩子的值 )。 这个时候的堆,我们叫做 最大堆 (每个节点值 都大于 它的孩子的节点的值 ),相应也可以定义出最小堆 !
总结: 最大堆:首先是个 完全二叉树,然后,每个节点的值都大于它的孩子节点的值!
标签:使用 快速 ati 完全 width 种类 定义 一课 inf
原文地址:https://www.cnblogs.com/zach0812/p/11831890.html