fm 梯度计算

标签：产生   info   sig   blog   超出   html   nbsp   tps   没有   

https://www.cnblogs.com/chenshihao/p/12040910.html

sigmoid 小结

优点

• sigmoid 是使用范围最广的一类激活函数，具有指数函数形状，它在物理意义上最为接近生物神经元。
• (0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数。
• sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。
• 当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。

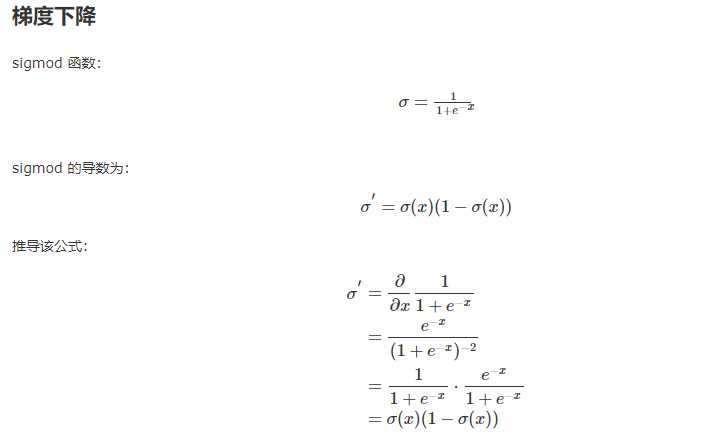
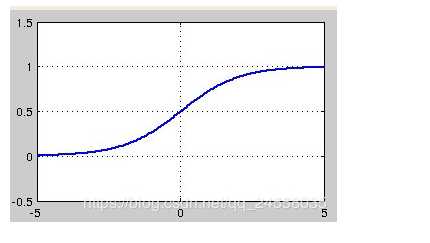
• Sigmoid函数的值域范围限制在(0,1)之间，我们知道[0,1]与概率值的范围是相对应的，这样sigmoid函数就能与一个概率分布联系起来了。

  缺点

• 最明显的就是饱和性。其两侧导数逐渐趋近于0 具有这种性质的称为软饱和激活函数。由于在后向传递过程中，sigmoid向下传导的梯度包含了一个 f′(x)因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f′(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。

• sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

fm 梯度计算

标签：产生   info   sig   blog   超出   html   nbsp   tps   没有   

原文地址：https://www.cnblogs.com/zhangbojiangfeng/p/12360776.html