标签:bsp 字符串 另一个 技术 div 遍历 mes length cout
编辑距离,又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将kitten一字转成sitting:
首先定义这样一个函数——edit(i, j),它表示第一个字符串的长度为i的子串到第二个字符串的长度为j的子串的编辑距离。
显然可以有如下动态规划公式:
思路:遍历s1数组,i表示处于s1位置,遍历s2用j表示所处位置,若s1的i位置等于s2的j位置,取前面凑的结果即可,即取s1的i-1凑j-1的结果,再分别用s1的前i-1去凑s2的j位置,和用s2的j-1去凑s1的i位置,和s1的i-1和s2的j-1位置之后修改一个字符,取小者。
输入:
abcf
dbfg
输出:
3
对abcf和abfg初试化都改为空需要编辑距离
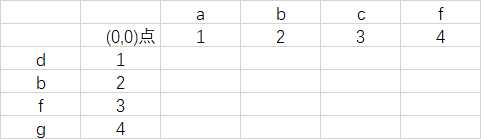
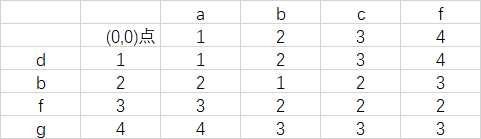
编辑距离过程表
#include <stdio.h> #include <iostream> #include <math.h> #include <string.h> #include <algorithm> using namespace std; const double PI=acos(-1.0); const int inf=0x7fffffff; int a[105]; int dp[105][105]; int n,m,mx,sum; int main(){ string s1,s2; cin>>s1>>s2; int al,bl; al=s1.length(); bl=s2.length(); for(int i=1;i<=al;i++){ dp[i][0]=i; //删除s1到前i位置需要编辑距离 } for(int j=1;j<=bl;j++){ dp[0][j]=j; //删除s2到前j位置需要编辑距离 } for(int i=1;i<=al;i++){ for(int j=1;j<=bl;j++){ if(s1[i-1]==s2[j-1]){ dp[i][j]=dp[i-1][j-1]; //s1的[i-1]位置等于s2的[j-1]位置,那用s1[i]凑s2[j]就取s1的前i-1凑s2前j-1的结果 } else{ dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;//表示取删除或替换或添加的编辑距离最小者 } //dp[i-1][j]表示用s1的前i-1凑s2的前j位置 } //dp[i][j-1]表示用s2的前j-1凑s1的前i位置 } cout<<dp[al][bl]; return 0; }
The struggle you‘re in today is developing the strength you need for tomorrow. Don‘t give up.
标签:bsp 字符串 另一个 技术 div 遍历 mes length cout
原文地址:https://www.cnblogs.com/xusi/p/12366680.html