标签：with   turn   阶乘   const   row   factorial   inf   tor   factor   

时间复杂度分析

大O表示法

• O(1): Constant Complexity 常数复杂度

 int n = 1000;
 System.out.println("Hey - your input is: " + n);

 int n = 1000;
 System.out.println("Hey - your input is: " + n); 
 System.out.println("Hmm.. I'm doing more stuff with: " + n);
 System.out.println("And more: " + n);

• O(log n): Logarithmic Complexity 对数复杂度

for (int i = 1; i < n; i = i * 2) 
{     
    System.out.println("Hey - I'm busy looking at: " + i); 
}

• O(n): Linear Complexity 线性时间复杂度

for (int i = 1; i <= n; i++)
{
    System.out.println("Hey - I'm busy looking at: " + i); 
}

• O(n^2): N square Complexity 平方

for (int i = 1; i <= n; i++) 
{
    for (int j = 1; j <=n; j++) 
    {         
        System.out.println("Hey - I'm busy looking at: " + i + " and " + j);     
    } 
}

• O(2^n): Exponential Growth 指数

int fib(int n) 
{
    if (n <= 2) 
    return n;     
    return fib(n - 1) + fib(n - 2); 
}

• O(n!): Factorial 阶乘

注意：只看最高复杂度的运算

时间复杂度分析

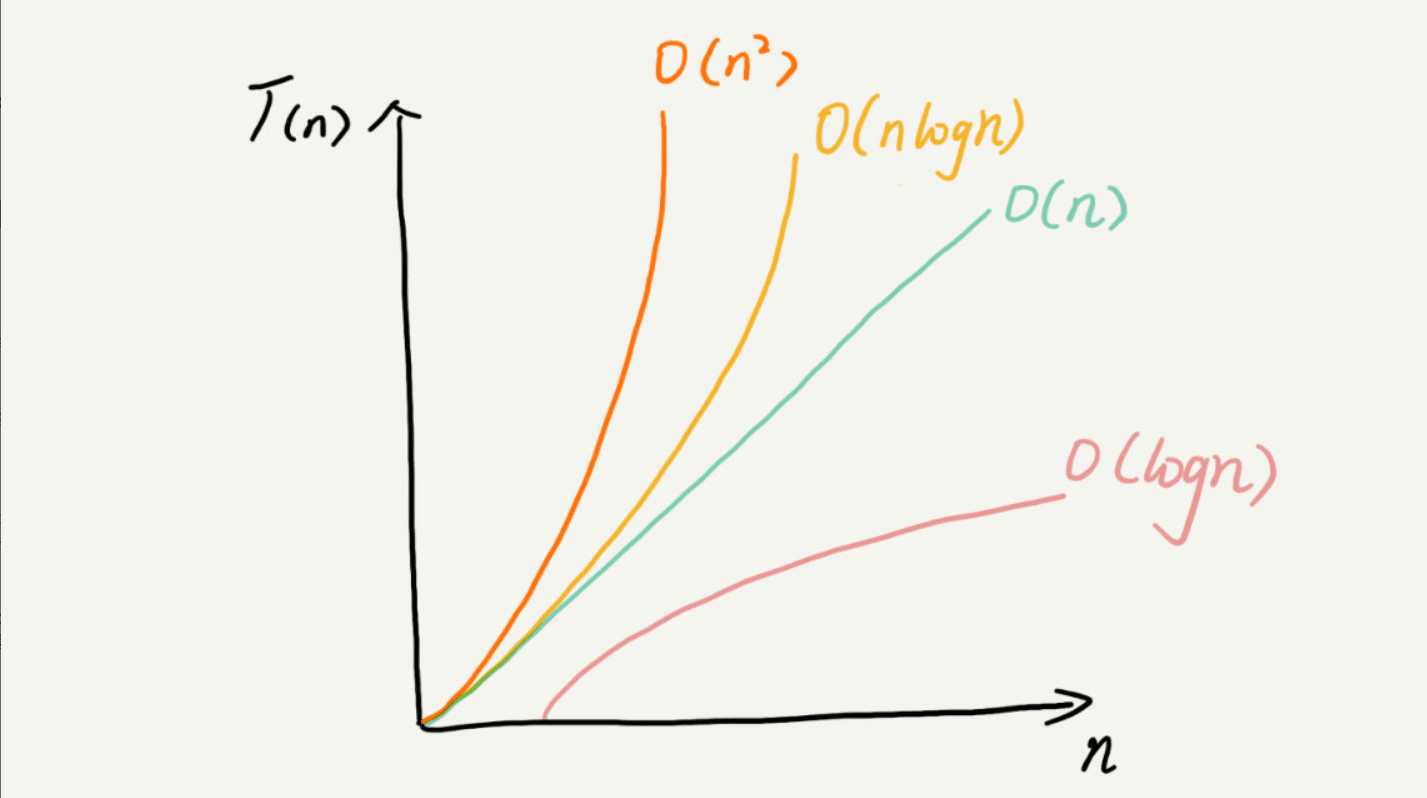
标签：with   turn   阶乘   const   row   factorial   inf   tor   factor   

原文地址：https://www.cnblogs.com/liugangjiayou/p/12369872.html