标签：search 插入数据 基本概念 out 最坏情况 gre parent 基本 static
1. 一些基本概念
（1）度
结点的度degree：结点的子树数
树的度：树里面各结点度的最大值
度为0的结点：叶结点 leaf 或终端结点 度不为0的：非终端结点、分支结点
（2）层次level
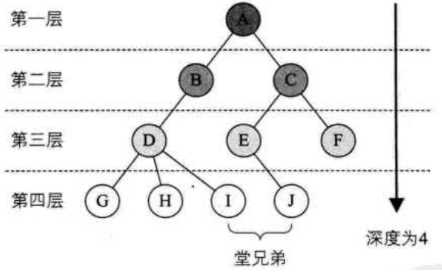
树的深度 depth、高度：层次最大值
二叉树深度：共N个结点
一般二叉树平均深度：O(根号N)
二叉查找树平均深度：O(log N)
最坏情况：N-1 斜二叉树
2. 二叉树
1.1 特殊二叉树
（1）满二叉树
所有分支结点都有左、右子树，且所有叶子都在同一层
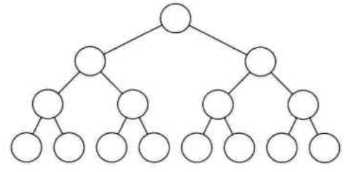
若有 k 层，则共：2^0 + 2^1 +...+ 2^(k-1) = 2^k -1 个结点
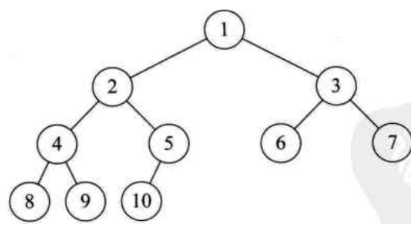
（2）完全二叉树
n个结点，深度为h，除了第 h 层外其它层结点数都达到最大个数，且第 h 层所有结点都集中在左侧
特点：
叶子结点只出现在层次最大的两层：h 层和 h-1 层
对任一结点，若其右子树最大层次为L，则其左子树最大层次为L或L+1
同样结点的二叉树，完全二叉树的深度最小
（3）二叉排序树Binary sort tree/二叉查找树
左子树 < 根 < 右子树，对其中序遍历结果是升序
（4）线索二叉树
（5）平衡二叉树/AVL树 Self-Balancing Binary Search Tree /Height-Balanced Binary Search Tree
左子树、右子树都是平衡二叉树，且每一个结点的左子树、右子树深度差绝对值小于等于 1
是高度平衡的二叉排序树
（6）红黑树
自平衡--二叉查找树
（7）赫夫曼树 Huffman Tree
最优树：带权路径长度WPL最小
1.2 二叉树性质
（1）第 i 层最多有 2^(i-1) 个结点
（2）深度为k的二叉树最多（满二叉树）有2^k -1个结点
（3）任二叉树，若其终端结点（度为０的）数为 a0 ,度为2的结点数为 a2，则 a0 = a2 + 1
设度为1的结点数为 a1，则树的结点数 n = a0 + a1 + a2
考虑连线的数目（从斜二叉树的角度去想），n个结点的二叉树有 n-1 条线，则 n-1 = 0*a0 + 1*a1 + 2*a2
（4）有n个结点的完全二叉树的深度为 [log2 n] + 1 [ x ]表示小于等于x的最大整数，即向下取整
对于满二叉树，若结点数为m，深度为k，则 m = 2^k -1 或 k=log2(m+1) 。一个同样深度的完全二叉树，其结点数小于等于2^k -1，但必大于2^(k-1)-1，则此完全二叉树的结点数n：
2^(k-1)-1<n≤2^k -1，即2^(k-1) ≤n<2^k 取对数，则 k-1≤log2n<k
（5）完全二叉树，n个结点，按层序编号（每层从左到右），对任一结点 i（1≤i≤n）有：
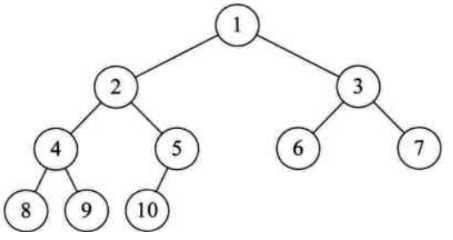
i == 1，i是根，无双亲 i>1，其双亲是 [i/2] 向下取整
2i>n，则i无左子 2i≤n，则其左子是2i
2i+1>n，则i无右子，否则其右子是2i+1
1.3 存储结构
（1）顺序存储
如完全二叉树的顺序存储：
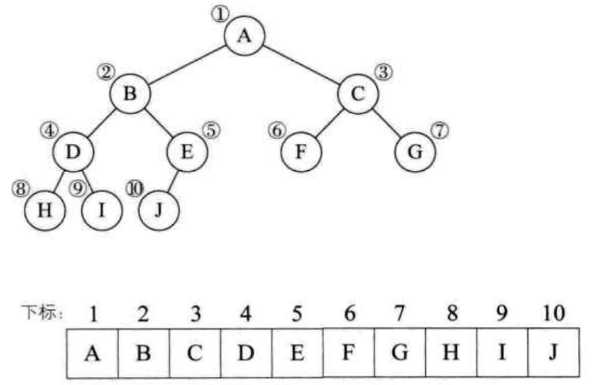
对于非完全二叉树，可将缺失的位置填上空，其他位置按完全二叉树的层级编号存储即可
对于右斜二叉树，深度k，节点数k，需要2^k -1 个存储单元，因此这种顺序存储只适合比较严格定义的完全二叉树
（2）链式存储---二叉链表
typedef struct BitNode { int data; struct BitNode *leftChild,*rightChild; };
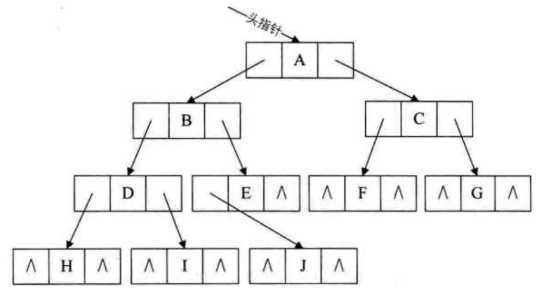
如果要从子结点找父结点，则可增加一个父指针域
1.4 二叉树遍历
（1）前序遍历
根---左---右
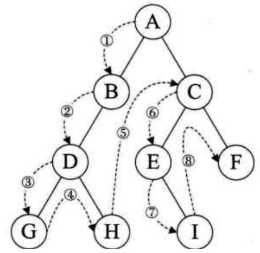
前序遍历：A B D G H C E I F
void preOrderTraverse(BitTree root) { if (root) { cout<<root->data<<endl; preOrderTraverse(root->leftchild); preOrderTraverse(root->rightchild); } }
（2）中序遍历
左--根--右
遍历结果：G D H B A E I C F
void inOrderTraverse(BitTree root) { if (root) { inOrderTraverse(root->leftchild); cout<<root->data<<endl; inOrderTraverse(root->rightchild); } }
（3）后序遍历
左--右--根
遍历结果：G H D B I E F C A
void postOrderTraverse(BitTree root) { if (root) { postOrderTraverse(root->leftchild); postOrderTraverse(root->rightchild); cout<<root->data<<endl; } }
（4）层序遍历
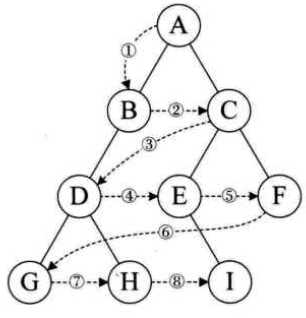
A B C D E F G H I
1.5 线索二叉树
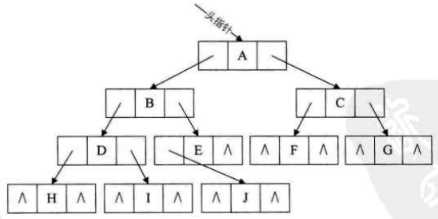
n个结点，则有2n个指针域；
有n-1条线，即n-1个指针域是有用的，则浪费了 2n-(n-1)=n+1个指针域
这里共10个结点，则浪费了11个结点
中序遍历：H D I B J E A F C G
根据遍历结果可知一个结点的前驱和后继，利用空的指针域来指向前驱或后继（这种指针就是线索）----构成线索二叉树：
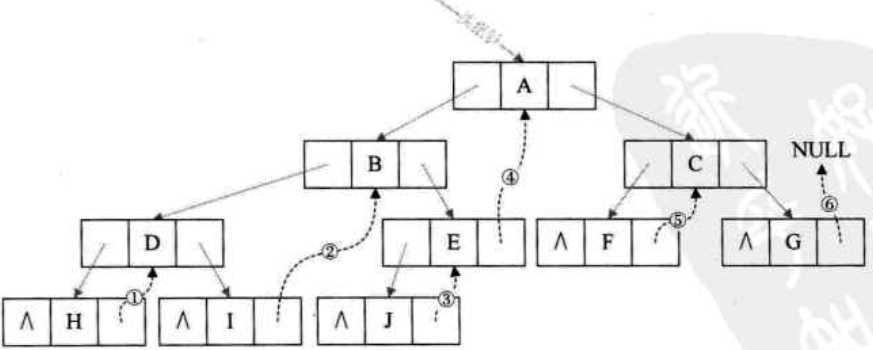
H的后继是D，则H的右指针指向D；D的后继是I，已经指向了I；I的后继是B，其右指针指向B............................
即利用右指针指向该结点的后继，本来有右子的结点，其右指针已经是指向其后继（在中序遍历中，右子是后继）。
再利用空的左指针指向前驱：
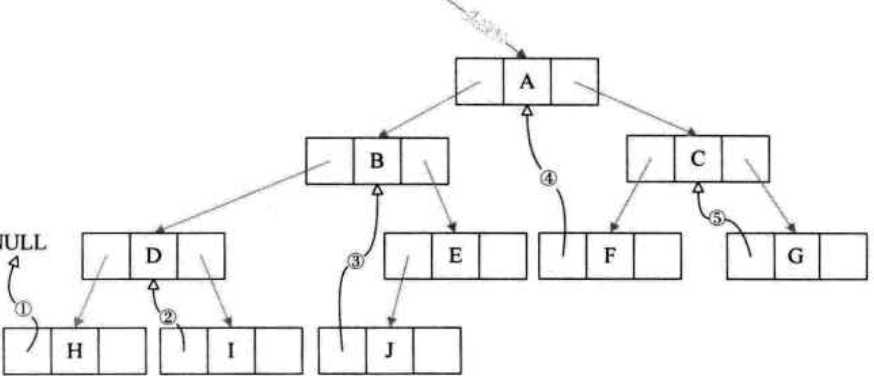
两种结合起来就变成了一个双向链表：
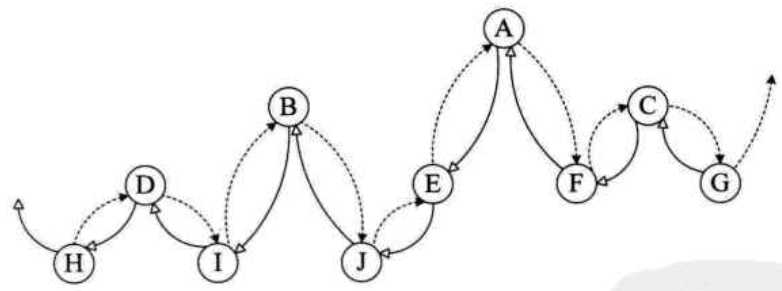
为了区分左子与前驱、右子域后继，还需要增加两个标志：lflag、rflag
增加了空间消耗，但是带来了访问、增删方便的优点
（1）结构
typedef enum {Link,Thread} PointerTag; //第一个枚举成员默认0，Link==0 表示左右子指针 // Thread==1，表示前驱、后继线索 typedef struct BitThrNode { int data; struct BitThrNode *lchild,*rchild; PointerTag ltag; PointerTag rtag; }BitThrNode,*BitThrTree;
（2）线索化
中序遍历过程中修改空指针域
pre和p就建立了前驱后继双向关系
static BitThrTree pre = nullptr; void InThreading(BitThrTree p) { if(p) { InThreading(p->lchild); if(!p->lchild) { p->ltag = Thread; p->lchild = pre; //指向前驱 } if(nullptr != pre && nullptr == pre->rchild) { pre->rtag = Thread; pre->rchild = p; //指向后继 } pre = p; //保持pre指向p的前驱 InThreading(p->rchild); } }
（3）
增加一个头结点，头结点左指针域指向根结点，右指针指向中序遍历最后的结点。中序第一个结点左指针域指向头结点，最后一个结点右指针指向头结点。
这样可从第一个结点起顺着后继遍历，也可从最后一个结点向前顺前驱遍历。
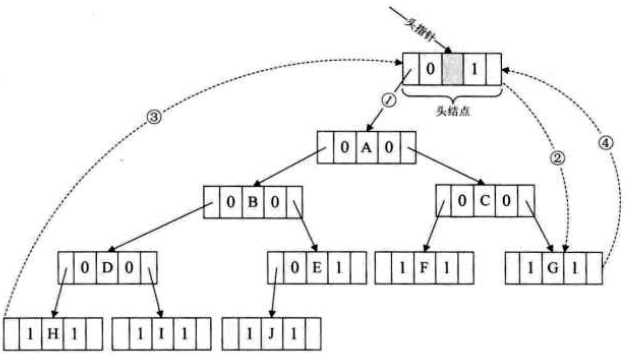
void InorderTraverse_Thr(BitThrTree t) { BitThrTree p = t->lchild; //p是根结点 if(nullptr == p) { return; } while(p != t) { while(p->ltag == Link) { p = p->lchild; //找到最左侧的结点，即中序遍历的第一个结点 } cout<<p->data<<endl; //操作该结点 while(p->rtag == Thread && p->rchild != t) { p = p->rchild; cout<<p->data<<endl; } p = p->rchild; } }
1.6 AVL树
（1）AVL树概念
高度平衡的二叉排序树
平衡因子Balance Factor:结点左子树深度减右子树深度 -1、0、1
最小不平衡子树：离插入结点最近的，且平衡因子绝对值大于1的结点为根的子树
查找、插入、删除：平均和最坏情况都是O(logn)
（2）二叉排序树---->AVL树
二叉排序树/二叉查找树 依据二分查找的思想，便于查找数据，但是插入数据时容易出现数据全部在某一遍的情况。
（3）导致不平衡的情况以及左旋、右旋
LL：插入新结点到根结点左子树的左子树，根的BF由1变为2 需要右旋
RR：插入新结点到根结点右子树的右子树，根BF由-1变为-2 需要左旋
LR：插入新结点到根结点左子树的右子树，根BF由1变为2 需要先左后右旋转
RL：插入新结点到根结点右子树的左子树，根BF由-1变为-2 需要先右后左旋转
右旋：插入结点时，结点倾向于左边 顺时针旋转
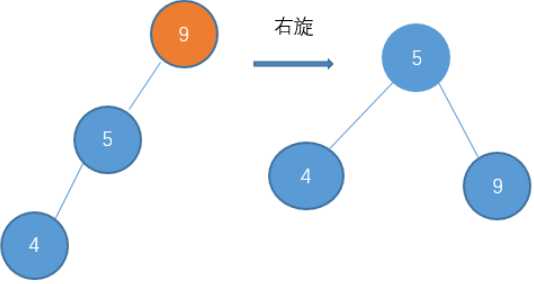
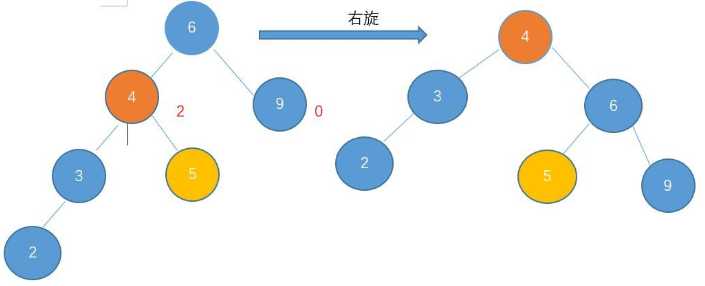
左旋：逆时针
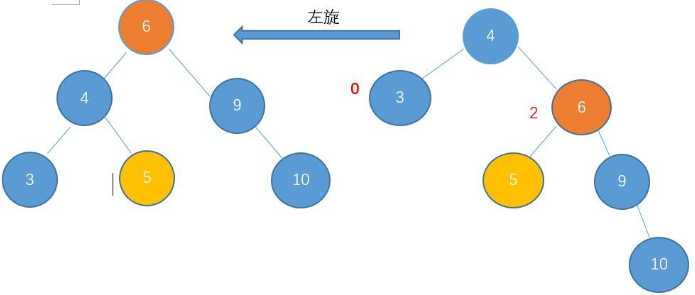
（4）AVL树实现
数组a[10]={3,2,1,4,5,6,7,10,9,8};
①构建二叉排序树，不旋转
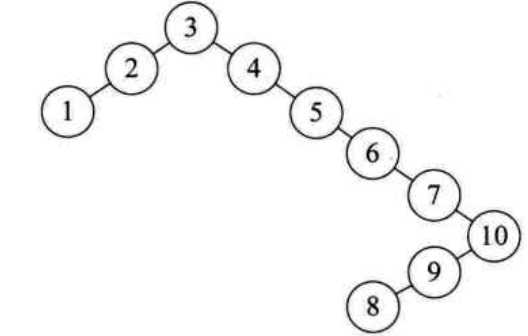
②AVL树插入过程
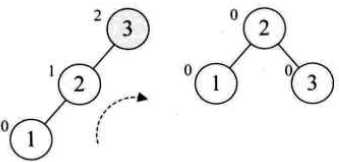
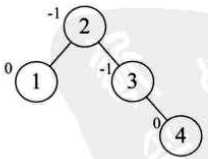
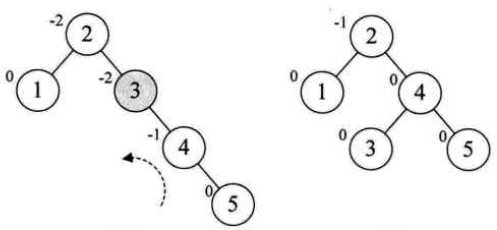
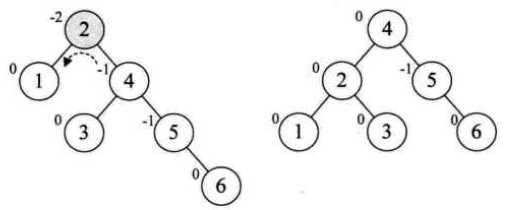
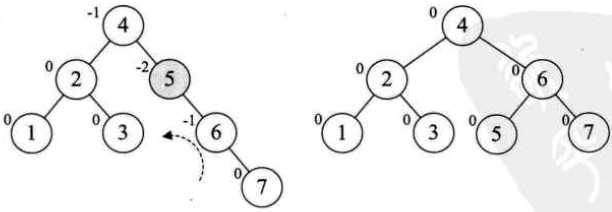
新插入结点9，结点7不平衡需要左旋，但是左旋后9变成了10的右子，不满足二叉排序树了。先对9、10右旋
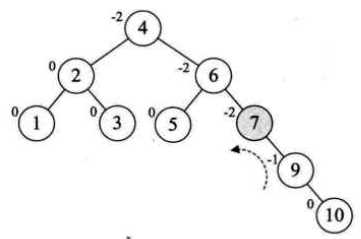
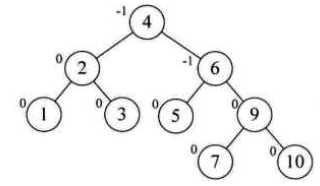
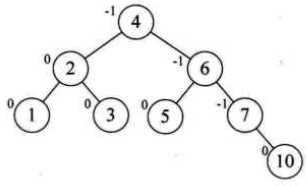
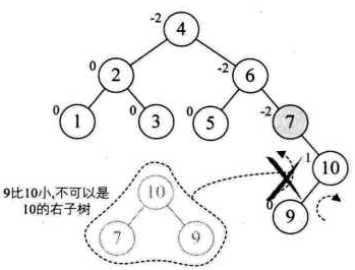
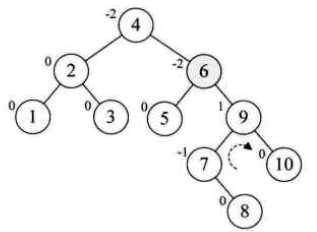新假如结点8,6的BF为-2，9的BF为1，需要对9右旋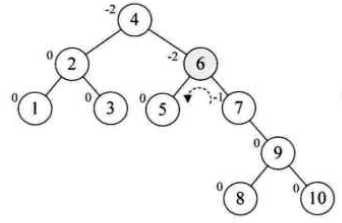 
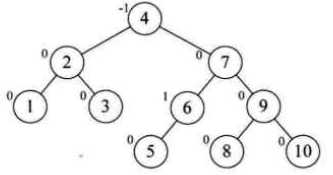
（5）Code
typedef struct BitNode { int data; int bf; struct BitNode *lchild,*rchild; }BitNode,*BitTree;
①右旋
主要有两个变化：原来根与其左子树的指向关系----->变成左子树指向根
原来根左子树的右子树变成了根的左子树
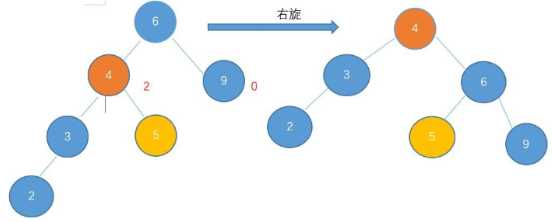在这里看，就是4和6关系的改变，以及5变成了6的左子树
void R_Rotate(BitTree *p) { BitTree tmp = (*p)->lchild; //先记下根左的位置，则根的左指向关系可以断开了 (*p)->lchild = tmp->rchild; tmp->rchild = *p; *p = tmp; }
②左旋
void L_Rotate(BitTree *p) { BitTree tmp = (*p)->rchild; (*p)->rchild = tmp->lchild; tmp->lchild = (*p); *p = tmp; }
③左平衡旋转处理
（6）
要查找的集合本身没有顺序，需要经常插入、删除操作，则需要构建AVL树。其查找、插入、删除复杂度都为 O(log n)
1.7 红黑树
（1）红黑树特点
①每个结点要么是红色，要么是黑色
②根结点为黑色
③叶子结点都是黑色，且为NULL
④连接红色结点的两个子结点都是黑色
⑤从任意结点出发到每个叶子结点，路径中包含相同数量的黑色结点
⑥新加入到红黑树的结点是红色结点
从根结点到叶子结点的最长路径不大于最短路径的2倍
（2）
红黑树是一种二叉查找树，但在每个节点增加一个存储位表示节点的颜色，可以是红或黑（非红即黑）。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍，因此，红黑树是一种弱平衡二叉树，相对于要求严格的AVL树来说，它的旋转次数少，所以对于搜索，插入，删除操作较多的情况下，通常使用红黑树。
1.8 赫夫曼树
（1）
权：结点右各自的权值
树的带权路径长度WPL：树中所有叶子结点带权路径长度之和
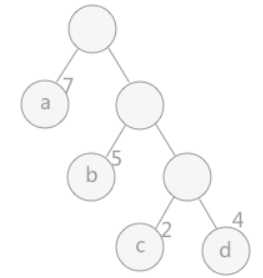WPL=7*1+5*2+2*3+4*3
WPL最小的树就是 最优二叉树/赫夫曼树
（2）构建
权值越大的点离根越近
①从n个结点中取出权值最小的两个结点，作为左右子树构成一个二叉树，且其根的权值为左右孩子权值之和
②在原来n个结点中去掉这两个结点，并将新生成的二叉树根的权值加到原来的行列中
重复①②直到只剩下一棵树
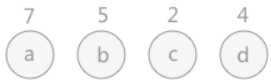
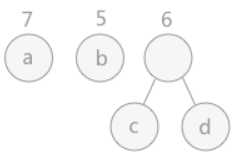
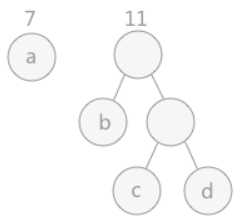
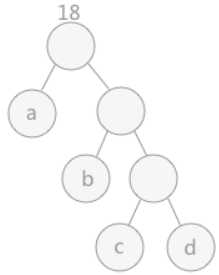
（3）Code
typedef struct { int weight; //权值 int parent,left,right; }HTNode,*HuffmanTree;
（4）赫夫曼编码
1.9 树树、森林、二叉树的转换
（1）树转换为二叉树
步骤：
①加线。所有兄弟结点之间加一条连线
②去线。对树中的每个结点，只保留它与它左孩子的连线，删除它与其他孩子结点之间的连线
③层次调整。以树的根结点为轴心，将整棵树顺时针旋转使之层次分明。
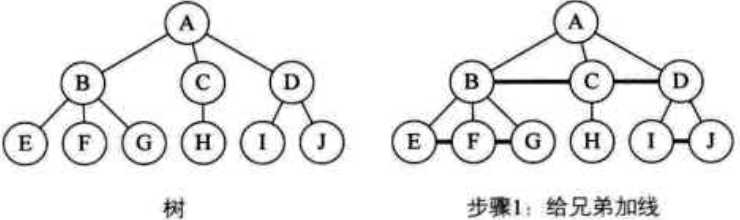
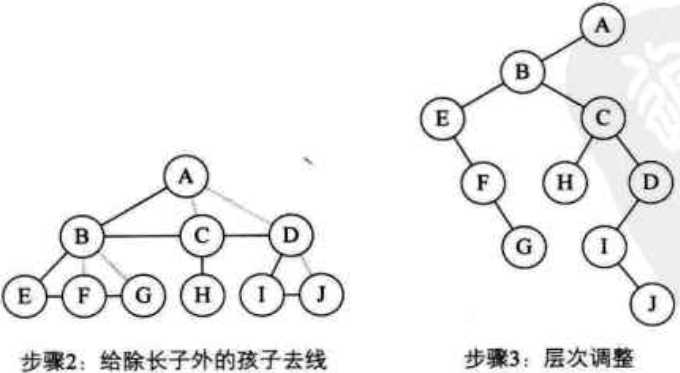
去线后，旋转。
B的兄弟C变成了B的右孩子。E的兄弟F变成了E的右孩子，F的兄弟G变成了F的右孩子
C的兄弟D变成C的右孩子。D的左孩子I不变，I的兄弟J变成了I的右孩子
（2）森林转换为二叉树
森林由很多树组成，可理解为森林中每一棵树都是兄弟。
步骤：
①把每棵树变成二叉树
②第一课二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子（因为树转换为二叉树后根结点是没有右孩子的如1.9）。
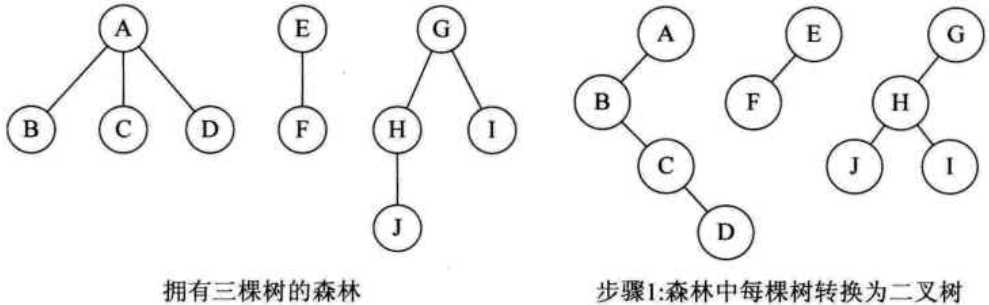
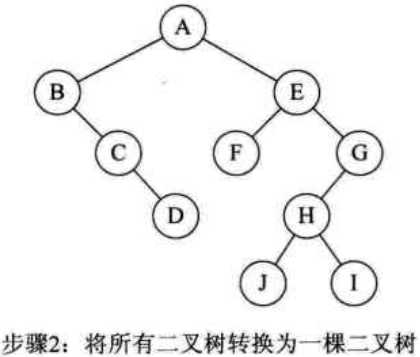
（3）二叉树转换为树
步骤：
①加线。将结点1的左孩子的所有右孩子结点作为结点1的孩子。
②去线。删除原二叉树中所有结点与其右孩子结点的连线
③层次调整
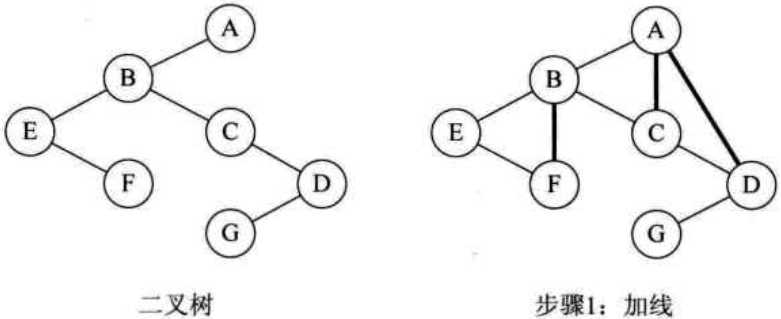
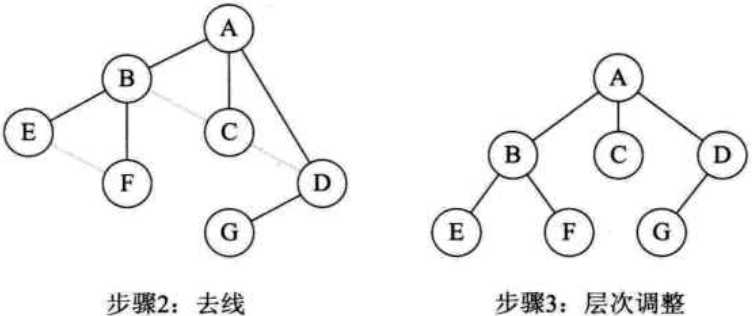
（4）二叉树转换为森林
能否转换为森林：根结点有右孩子就能转换为森林
步骤：
①从根结点开始，若右孩子存在，则删除与右孩子的连线，查看分离后的二叉树，若根结点右孩子存在则删除连线.....，直到所有右孩子连线都删除为止
②将各个树转换为二叉树
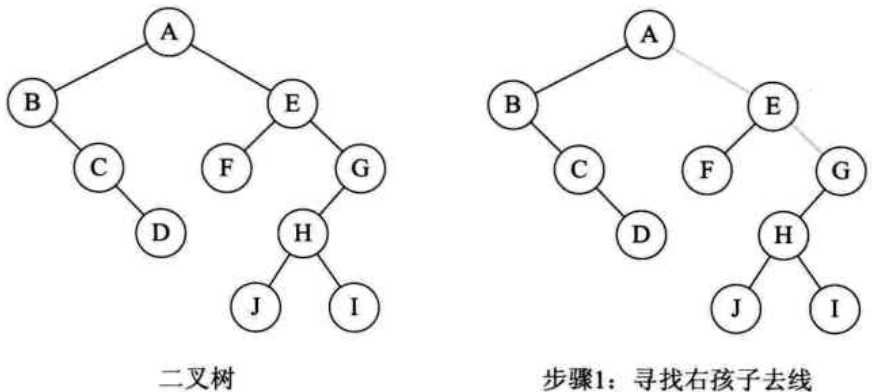
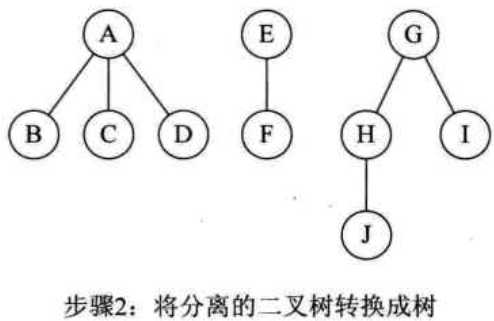
（5）树与森林的遍历
树的遍历：
①先根遍历。先访问根结点，然后依次先根遍历根的每棵子树
②后根遍历。先依次后根遍历每棵子树，然后访问根结点
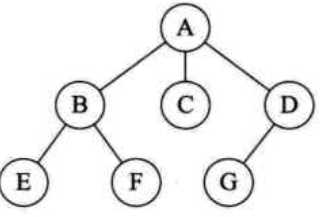
先根遍历：ABEFCDG 后根遍历：EFBCGDA
森林的遍历：
①前序遍历。先对第一个树先根遍历，然后第二棵树...
②后序遍历。对第一棵树后跟遍历，然后第二棵树...
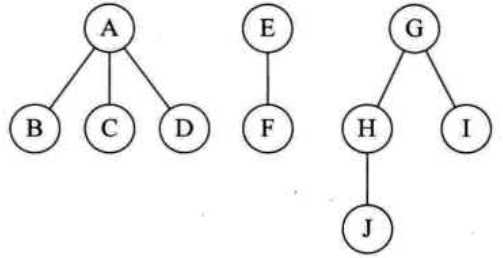
先序：ABCDEFGHJI 后序：BCDAFEJHIG
这个森林对应的二叉树：
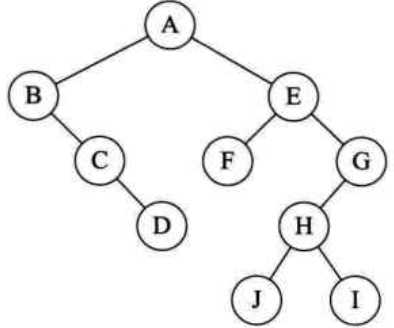
前序遍历：ABCDEFGHJI 中序遍历：BCDAFEJHIG
森林的先序遍历与对于二叉树的前序遍历相同，而森林的后序遍历与对于二叉树的中序遍历相同
标签：search 插入数据 基本概念 out 最坏情况 gre parent 基本 static
原文地址：https://www.cnblogs.com/taoXiang/p/12254108.html
