标签:重建 nal blog isp super ati work using 出现
https://cs.stanford.edu/people/jcjohns/eccv16/
官方源码Torch:https://github.com/jcjohnson/fast-neural-style
其他程序Tensorflow:https://github.com/lengstrom/fast-style-transfer,实现细节略有不同
这篇主要讲一下感知损失在图像变换问题(image transformation),如风格迁移和单幅图像超分辨率重建中的应用。感知损失是由预训练模型提取的高层图像特征之间的差异。
2020年注定是不平凡的一年,希望能早日战胜病毒,早日返校继续科研。(其实是想出去玩,卷家里要疯啦!!!)
很多传统问题都可以归结为图像变换问题,解决该问题的一种方法是以有监督的方式训练一个前馈卷积神经网络,用像素损失度量输出与真实图像间的不同,在测试时很有效(速度快),但像素损失并没有捕捉两者间的感知属性。与此同时的一些工作表明,可以用感知损失生成高质量的图像,已经应用到多个领域,但是推理时速度慢(基于优化的方法)。
也就是说像素损失在测试时有速度有效,感知损失在图像质量上有有效。本文即结合两者的优点,预训练的损失网络loss network提取图像高层特征计算感知损失函数,该损失训练变换网络transformation network执行图像变换任务。
本文网络结构如下图所示,系统包含两部分:图像变换网络$f_{w}$和损失网络$\phi$, $\phi$在训练变换网络时是固定参数的。先前工作认为:针对图像分类的预训练CNN网络已经学会了对感知和语义信息进行编码,而这正是本文损失网络所要度量的。
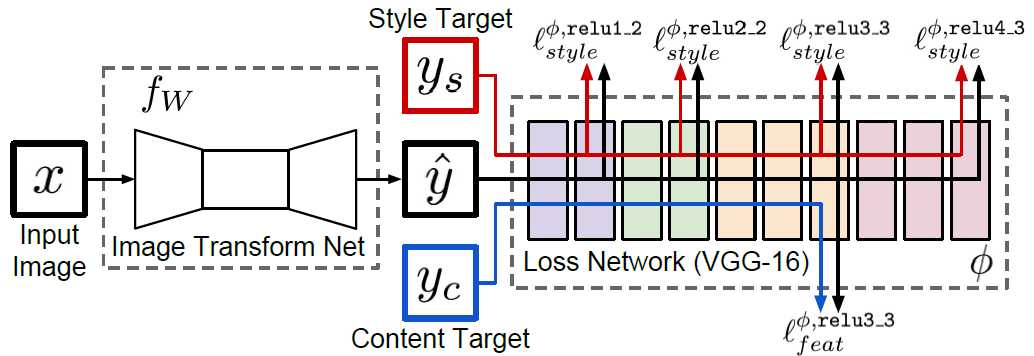
损失网络$\phi$定义特征重建损失$l_{feat}^{\phi}$和风格重建损失$l_{style}^\phi$,度量图像间内容和风格差异。对于每个输入图像$x$都有一个内容目标$y_{c}$和风格目标$y_{s}$。在风格转换中$x=y_{c}$。在超分中没有风格目标,输入图像为低分辨率图像,内容目标为真实的高分辨率图像。
图像变换网络的结构大致遵循DCGAN提出的指导意见。没有使用任何池化层,而是使用步进(反)卷积执行下采样和上采样(程序中即是通过设置步长,同时进行卷积操作和特征图空间尺寸的变化)。网络主体使用文献44的结构,包含5个残差块。输出层用tanh使输出图像像素值为[0,255]。除第一层和最后一层使用9×9的卷积核,其他卷积层使用3×3。
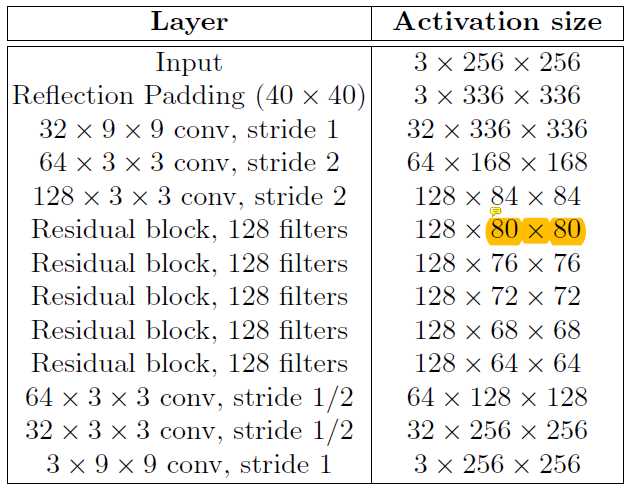
进行风格迁移的网络结构如下图。残差块中尺寸减少是因为残差块中的卷积去掉了零填充,恒定连接的时候以输入图谱的中心进行裁剪到相同尺寸。使用5个残差块,尺度减少了2×2×5=20,所以需要在网络输入时进行40×40的零填充,以使输入和输出尺寸都是256。图中的conv后接BN和ReLU。
进行超分的的网络结构如下图。
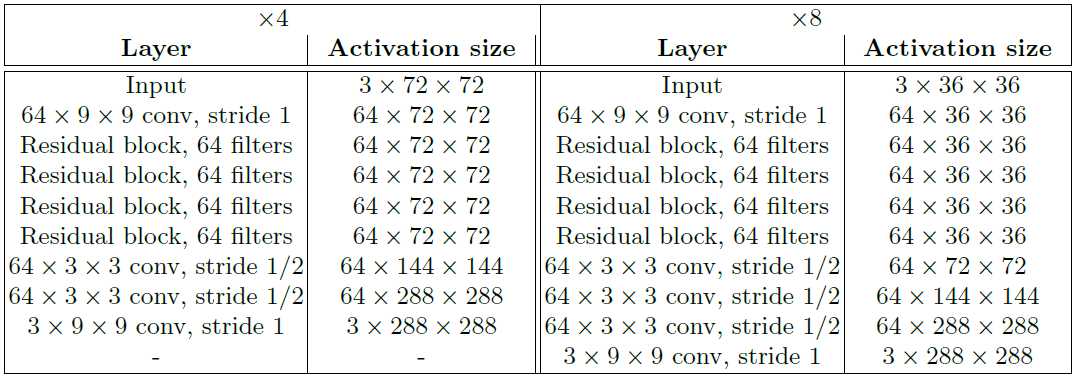
输入和输出。对于风格迁移3×256×256,超分输出为3×288×288,输入为$f$倍缩小。变换网络为全卷积,测试时可以为任意大小。
下采样和上采样。
对于风格迁移,变换网络先使用两个步长为2的卷积进行下采样输入图像,然后经过几个残差块,再经过两个步长为1/2的步进卷积。使用先进行下采样再上采样结构的好处:1.计算方面,对于相同的计算代价,下采样后可以使用更大的网络(更多的卷积核)。例如,输入图像为C×H×W,一个核为3的卷积核就应该是C×3×3,其与输入图像进行一次计算时需要9C乘法和9C加法(对应通道数进行计算,每个通道上的滤波器上对应元素相乘再相加,即9次乘法,8次加法,C个通道即再乘以C。然后通道间相加,再加偏置,即又有C次加法)。为了得到同样大小的特征图谱(进行填充),即需要用上述过程计算HW个数,此时就9CHW次乘法和9CHW次加法。又有这样的卷积核C个,即最终需要9C2HW次乘法和9C2HW加法。而参数量为9C2,这里是输入和输出通道数均为C。2.有效感受野大小,高质量的风格转换需要以连贯的方式更改图像的大部分,这就需要输出中的每个像素对于输入图像中更大的感受野。没有下采样,每个卷积操作以2倍的大小增加感受野范围,使用D因子的下采样时就以2D倍增加感受野。使用相同的层数可以获得更大的感受野。
对于超分,假设上采样率是f,即尺寸扩大f倍,变换网络使用几个残差块,然后接log2f个步长为1/2的步进卷积(具体程序中应该是反卷积)。与文献1使用双线性插值上采样低分输入图像在送给网络不同。使用步进卷积的好处是可以和网络的其他部分联合训练,而使用固定的上采样函数就没有这样的作用。
残差连接。本文方法所使用的残差块如下,去掉了resnet v1中加和后的ReLU激活。
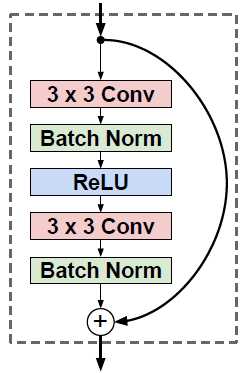
损失网络$\phi$是在ImageNet上预训练的VGG16。
特征重建损失。$\phi_{j}(x)$表示损失网络第j层的激活,如果j是卷积层,那么$\phi_{j}(x)$是形状为Cj×Hj×Wj的特征图谱,特征重建损失为特征表示间的欧式距离:$l_{feat}^{\phi,j}(\hat y,y)=$ $\frac {1}{C_{j}H_{j}W_{j}}$ $\Vert \phi_{j}(\hat y)-\phi_{j}(y) \Vert _{2}^{2}$
如下图,实验发现使用浅层的特征构造特征重建损失往往会产生于目标相似的图像。当使用更高层特征进行重建时,图像内容和整体空间结构得以保留,但颜色、纹理和精确形状却未被保留。使用特征重建损失可以是生成图像与目标感知上相似,但不必要求完全匹配。

风格重建损失。当内容出现偏差时特征重建损失进行惩罚,当样式如颜色、纹理和图案出现不同时,使用风格重建损失,格拉姆矩阵可以计算两两特征之间的相关性,所有它可以把握图像的大体风格。定义一个大小为Cj×Cj的格拉姆矩阵$G_j^\phi(x)$,其中每个原始值由如下公式给出:
$G_{j}^{\phi}(x)_{c,{c‘}}=$ $\frac {1}{C_{j}H_{j}W_{j}}$ $\sum_{h=1}^{H_j} \sum_{w=1}^{W_j}\phi_j(x)_{h,w,c}\phi_j(x)_{h,w,{c‘}}$
如果将特征图谱$\phi_j(x)$视为一个C维的向量,其中每个元素是Hj×Wj中每个值组成的一个行向量,即将$\phi_j(x)$转换为一个Cj×HjWj的二维矩阵$\psi$,再计算与其自身转置就内积,即为格拉姆矩阵:$G_j^\phi(x)=\psi\psi^T/C_jH_jW_j$。
风格重建损失由输出和目标图像格拉姆矩阵差异的F范数的平方表示,如下式$l_{style}^{\phi,j}(\hat y,y)=$ $\Vert G_j^\phi(\hat y)-G_j^\phi(y) \Vert _{F}^{2}$ 。即使两者的尺寸不一样,也可以计算,因为格拉姆矩阵的维度至于通道数相关。
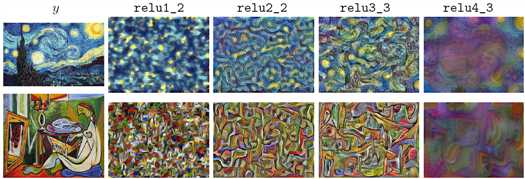
如下图,使用样式重建损失生成的图像保留了目标图像的样式特点,但是没有保留空间结构。利用越高层的特征构造样式损失,与目标图像的结构变化就越大。最终样式损失由每一层的损失之和组成。
[1] Dong, C., Loy, C.C., He, K., Tang, X.: Image super-resolution using deep convolutional networks. (2015)
[44] Gross, S., Wilber, M.: Training and investigating residual nets. http://torch.ch/blog/2016/02/04/resnets.html (2016)
Perceptual losses for real-time style transfer and super-resolution(by_xiao jian)
标签:重建 nal blog isp super ati work using 出现
原文地址:https://www.cnblogs.com/lab210/p/12386320.html