机器学习---归纳学习

标签：大脑   就是   png   特殊性   一致性   数据分布   判断   过拟合   也有   

人类的学习：经验→（大脑思考）→规律

机器的归纳学习：数据→（学习算法）→模型

所以说学习算法是一个模拟人类大脑思考的过程。

1）数据：

数据存储于计算机中，以训练集D的形式存在，D=｛x₁ ，x₂ ，... ，x_m｝其中x_1~m为m个样本（示例）。

样本x _i =｛x_i1，x_i2，...，x_id｝→产生d维样本（示例、输入）空间。

有监督：则y _i 为x _i 的标记，y _i 的集合→标记（输出）空间。

x _i +y _i →（x _i ，y _i ）称为样例。

2）学习算法：

目的：由训练集学习出从输入（样本、示例）空间到输出（标记）空间的映射 x → y 模型。

流程：假设空间→（与训练集一致）→版本空间→（归纳偏好）→模型

在全部的假设空间中，与训练集一致的很可能不止一个，这些都与训练集一致的假设空间就构成了版本空间。

在众多的版本空间里，需要进一步筛选出最符合实际情况的模型，就得依靠归纳偏好（模型评估与选择）了。

那么问题来了，如何判断训练出的模型与实际的拟合程度呢？答案是误差分析。

误差的分析：

　　1.留出法：将训练集D在分层采样（保证数据分布一致性）的条件下N次划分为样本集S和测试集T，结果取平均值，注意，在这里，S、T的划分是有讲究的，若S过多，T过少，得出的误差结果则不够准确，若S过少，T过多，训练出的模型则不够准确，一般划分为S:D=2/3 or 4/5，为了摆脱S:T的误差，可以使用留一法：设共有K个样本，将K-1个样本作为训练集，余下一个作为测试集，反复测试K次取平均值，但是，这个方法也有个困扰，那就是在样本很多的情况下去采用留一法很费时间，不切实际，另外，留一法也未必永远比其他方法准确。

　　2.交叉验证法：将样本集D进行N次划分为K个分层采样的子集，每次采用K-1个作为训练集，余下一个作为测试集，结果取平均值，故也称为N次K折交叉验证，其实留一法就是只有一个子集（为全集）的N次M折交叉验证。

　　3.自助法：给定包含m 个样本的样本集D ， 每次随机从D 中挑选一个样本，将其拷贝放入D ‘ 然后再将该样本放回数据集D 中，重复执行m 次后，就得到了包含m个样本的数据集D ‘，而D 中有一部分样本会在D ‘中多次出现，而另一部分样本不出现。

不被选中的概率为：

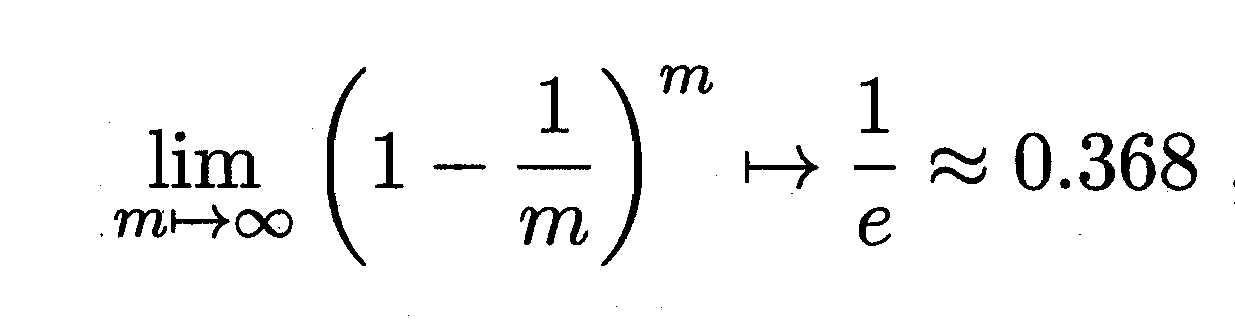
 将未被选到的数据（约1/3）用作测试集，这样得到的结果也称为包外估计。但自助法改变了数据集的分布，会产生偏差，所以数据较多时更常使用留出法/交叉验证法。

机器学习将训练集上的误差称为训练误差，将测试集上的误差称为测试误差，新对象应用该模型产生的误差称为泛化误差，我们不能得到泛化误差，只能用测试误差来近似。

注意：训练集具有普适的一般性质和特定于该训练集的特殊性质，若模型未能训练到得到一般性质，则成为欠拟合，反之，若训练得过度了，连特殊性质也学来了，那就是过拟合。

举个例子，若训练集是一些红苹果，若测试集给出的是一棵苹果树，欠拟合会误将整个苹果树识别为苹果，若测试集是一个青苹果，过拟合会误将青苹果识别为不是苹果，可见欠/过拟合都不能对对象进行正确的归纳，测试误差过高/过低都是不适宜的。

TBD

机器学习---归纳学习

标签：大脑   就是   png   特殊性   一致性   数据分布   判断   过拟合   也有   

原文地址：https://www.cnblogs.com/shenminghe/p/MachineLearning_IndustiveLearning.html