张正友平面定标法

标签：二维矩阵   height   结构   旋转   nbsp   角度   小型   地方   不同的   

图像坐标系与物理坐标系

在数字图像处理中，一副二维图片由一个二维矩阵表征。矩阵元素所在的位置即为该点坐标，矩阵元素的大小即为像素值的大小。但是，图像坐标系是离散的且没有物理尺寸，无法和现实世界建立联系。因此，我们引入物理坐标系。

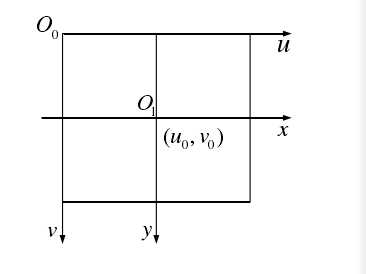
如上图，u和v是图像坐标系的轴，O₀为其原点。物理坐标系以图像坐标系的O₁（u₀，v₀）为原点，x，y轴分别平行于u，v轴。设dx，dy为单位像素在x和y方向上的尺寸。其中，u₀，v₀，dx，dy为相机的内参。由上述可得，物理坐标系中的坐标（u，v）有：

u = x/dx + u₀，v = y/dy + v₀　　　　　（1）

将（1）式变成矩阵形式，有：

相机坐标系与世界坐标系 

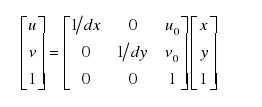
与上述两个二维坐标系不同，相机坐标系O_c-X_cY_cZ_c属于三维空间坐标系。其中，O_c为光心，Z_c为光轴，X_c与Y_c分别平行于物理坐标系的x和y轴。相机在不同的地方对场景进行拍摄，每个视角下的场景都以该视角下的相机坐标系为参考坐标系，这就造成了现实世界中的同一点在不同的相机坐标系中有着不同的坐标。所以，构建一个三维坐标系——世界坐标系O_w-X_wY_wZ_w，用于标识不同视角下各相机坐标系的相对位置。

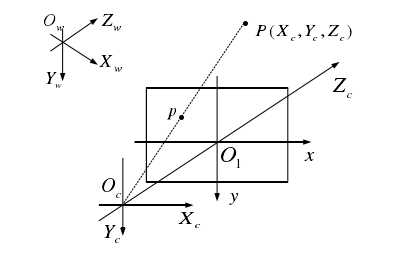
物理坐标系，相机坐标系和世界坐标系如上图所示。其中O_cO₁的长度为相机的焦距。有一点P，其在相机坐标系的坐标为（X_c，Y_c，Z_c），在世界坐标系的坐标为（X_w，Y_w，Z_w），则有变换矩阵，使得：

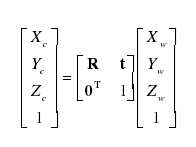
其中，R为旋转矩阵，表示两系的旋转关系；t为平移向量，表示O_c和O_w之间的相对位置。

相机几何模型

现有三维空间中的点P（X_c，Y_c，Z_c）投影到成像面上的点p（x，y）。设f为相机的焦距。

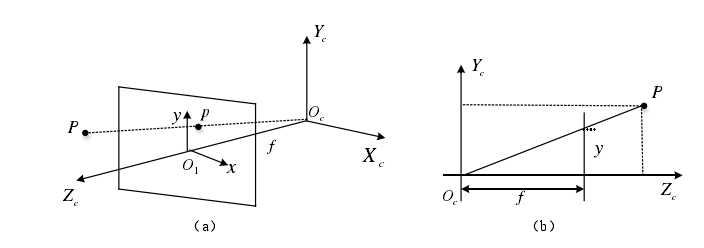
则根据相似三角形有：

x = fX_c/Z_c，y = fY_c/Z_c　　　　（2）

将（2）式变成矩阵形式，有：

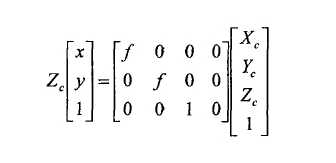
则由式（1），（2）得：

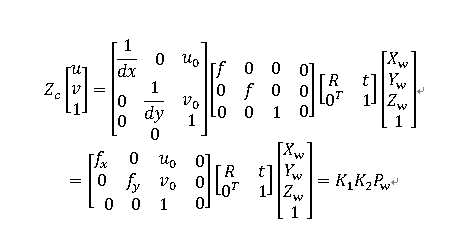
其中，f_x = f/dx，f_y = f/dy，分别为相机在x轴和y轴方向上的焦距。矩阵K₁由相机内部参数f_x，f_y，u₀，v₀决定，矩阵K₂由外部参数R和t决定。

张正友平面定标法

该方法的标定物是一副黑白棋盘格，称其为标定盘。如下图：

内角点：上图中每四个黑白格中间的角点

由前述可得：

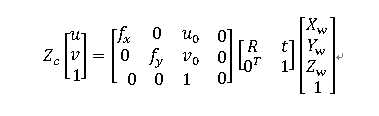
在该算法中，以标定盘上第一个内角点为参考系的原点，Z_w轴垂直于标定板所在平面，即标定板位于Z = 0平面上。令λ=1/Z_c，则有：

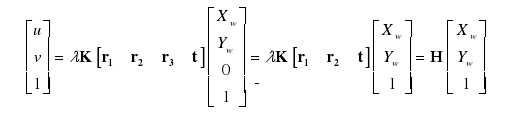
其中H = [h₁  h₂  h₃] = λK[r₁  r₂  t]，称H为单应矩阵。则有：

r₁ = (1/λ)K^-1h₁，r₂ = (1/λ)K^-1h₂

由旋转矩阵的单位正交性，即每列模长为1，不同列相互正交得：

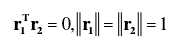
上下两式联立可得：

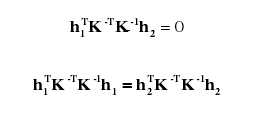
上述两式是关于内部参数的两个基本约束。

设矩阵A：

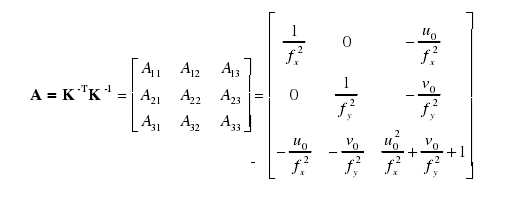
由上式可知，矩阵A是一个对称矩阵，则令向量a：

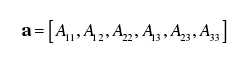
则有：

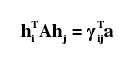
其中γ_ij^T  = [h_i1h_j1h_i1h_j2 + h_i2h_j1h_i2h_j2h_i3h_j1 + h_i1h_j3h_i3h_j2 + h_i2h_j3h_i3h_j3]^T 

这里如此设计γ_ij^T 的原因我也不清楚。但经过简单验算便可知道，上式的确是相等的。

 由内部参数的两个基本约束得：

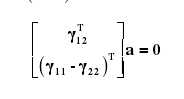
 若有n张不同角度的标定板图片，则有矩阵V（2n X 6）：Va = 0

由上述，即可求得内参K。

由H  =  λK[r₁  r₂  t]得，

K^-1H = λK[r₁  r₂  t]

则令N = K^-1H  = [n₁  n₂  n₃]，有：（旋转矩阵的列向量模长为1）

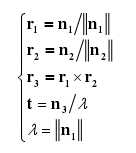
至此，求得外参R和t。

 参考论文： 

（1）基于结构光的小型物体三维重建技术_高爽

（2）Flexible camera calibration by viewing a plane from unknown orientations

张正友平面定标法

标签：二维矩阵   height   结构   旋转   nbsp   角度   小型   地方   不同的   

原文地址：https://www.cnblogs.com/ctqchina/p/12394907.html