标签：ima   平面   image   多分支   play   组件   elseif   splay   cas   

圈复杂度：在软件测试的概念里，它用来衡量一个模块判定结构的复杂程度，数量上表现为线性无关的路径条数，即 合理的预防错误所需测试的最少路径条数。

圈复杂度大说明程序代码可能质量低且难于测试和维护，根据经验，程序的可能错误和高的圈复杂度有着很大关系。

圈复杂度的原理：（其实就是分支的个数）

圈复杂度为1，意味着代码只有一条路径。
对于有一条分支的代码，它的圈复杂度为2。

• 从1开始，一直往下经过程序。
• 一旦遇到以下关键字，或者其它同类的词，就 +1。
  如 if、while、repeat、for、and、or。
• 给case语句中的每一种情况都 +1。

计算方法

程序的控制流图

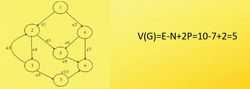
计算公式1：
\[V(G)=e-n+2p\]

式中：e表示控制流图中边的数量，n表示控制流图中节点的数量，p表示图的连接组件数目（图的组件数是相连节点的最大集合）。
因为控制流图都是连通的，所以p为1.

模块的控制流图

计算公式2：
\[V(G)=区域数=判定节点数+1\]

其实，圈复杂度的计算还有更直观的方法，因为圈复杂度所反映的是“判定条件”（如 if、while等）的数量，所以圈复杂度实际上就是等于判定节点的数量再加上1，也即控制流图的区域数。

注意：对于多分支的CASE结构或IF-ELSEIF-ELSE结构，统计判定节点的个数时需要特别注意一点，要求必须统计全部实际的判定节点数，也即每个ELSEIF语句，以及每个CASE语句，都应该算为一个判定节点。

复杂的控制流图

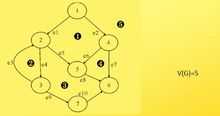
计算公式3：
\[V(G)=R\]

式中：R代表平面被控制流图划分成的区域数。

总结：

• 针对程序的控制流图时，最好还是采用第一个公式，即 V(G)=e-n+2；
• 针对模块的控制流图时，可以直接统计判定节点数，这样更为简单；
• 针对复杂的控制流图时，使用区域计算公式V(G)=R更为简单。

【软件测试】圈复杂度

标签：ima   平面   image   多分支   play   组件   elseif   splay   cas   

原文地址：https://www.cnblogs.com/blknemo/p/12404273.html