标签:输入格式 方法 add 初始 方式 表示 load 多少 png
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:\(n\)个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师再次吹哨子时,传球停止,此时,拿着球没有传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了\(m\)次以后,又回到小蛮手里。两种传球方法被视作不同的方法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有三个同学\(1\)号、\(2\)号、\(3\)号,并假设小蛮为\(1\)号,球传了\(3\)次回到小蛮手里的方式有\(1\)->\(2\)->\(3\)->\(1\)和\(1\)->\(3\)->\(2\)->\(1\),共\(2\)种。
一行,有两个用空格隔开的整数\(n,m(3 \le n \le 30,1 \le m \le 30)\)。
\(1\)个整数,表示符合题意的方法数。
3 3240%的数据满足:\(3 \le n \le 30,1 \le m \le 20\)
100%的数据满足:\(3 \le n \le 30,1 \le m \le 30\)
2008普及组第三题
首先这道题我们应该能看出来是一道递推题。再仔细一看,这就是dp!
我们来找找规律。这里有点纠结的是环问题(不是图论的那个),这里我们采用倍长法。啥意思呢?看下(假设1号是小蛮。):
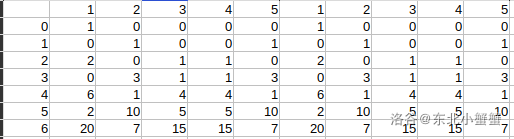
这是n=5时的传球情况。横着的表示同学编号,其中1是小蛮本人,竖着的代表传了多少次球,0表示初始状态。而表格中的数,代表传了多少次球传到当前同学的方案数。就设它是\(dp_{i,j}\)把,其中\(i\)代表传球次数,\(j\)代表当前同学编号。
首先初始状态下,小蛮接收到球的方案数显然是1,也就是不传这个方案,其他同学接到球的方案都是0,因为小蛮还没把球传给别人。此时小蛮拥有了1种让球回到自己身上的方案。
如果进行了1次传球,小蛮只能给相邻的5号和2号,所以进行1次传球的情况中,只有2号同学和5号同学都有1种方案,其他都是0。此时小蛮拥有了0种让球回到自己身上的方案。
如果进行了2次传球,2可能会还给1(小蛮),也可能会给3号。5可能会还给1(还是小蛮),也可能会给4号,也就是说3和4都各自有1种方案。但是小蛮此时可能会收到来自2的,也可能是来自5的,于是小蛮拥有了2种求回到自己身上的方案。
这么分叉下去好像有点乱,是到找规律的时候了。我们发现,一个人被传到的方案数是上一轮中和这个人相邻的两个人传球的方案数之和。为什么呢?因为球只能相邻之间传,所以要不然上一轮左边那个给我,要不然右边那个给我,方案数自然是两者之和,不多不少。
稍等,我还没解释什么是倍长法。只要你有眼睛如果你足够细心会发现上面那个表里面队列出现了两次。这其实是为了把尾部和头部衔接。实际编码中我们不需要这么做,加个特判就ok了,这其实只是一个更好理解的方法。
总结一下,
\[
dp_{i,j}=\begin{cases}1&i = 0, j = 1\\0&i = 0\\dp_{i - 1, n} + dp_{i - 1, 2}&j = 1\\dp_{i - 1, n - 1} + dp_{i - 1, 1}&j = n\\dp_{i - 1, j - 1} + dp_{i - 1, j + 1}\end{cases}
\]
此为不严谨写法,这个等式的优先级按照从上到下排列,如果上面的下面的式子同时满足后面的条件,取上面的。
那个表我是用Excel打的,这是我每一个区域的计算公式(不懂直接跳过就可以了),供参考。
=IF(COLUMN()<=6,IF(COLUMN()<>2,INDIRECT(ADDRESS(ROW()-1,COLUMN()-1))+INDIRECT(ADDRESS(ROW()-1,COLUMN()+1)),INDIRECT(ADDRESS(ROW()-1,COLUMN()+1))+INDIRECT(ADDRESS(ROW()-1,6))),INDIRECT(ADDRESS(ROW(),COLUMN()-5)))
/*
* @Author: crab-in-the-northeast
* @Date: 2020-03-03 21:36:03
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-03-03 23:12:37
*/
#include <iostream>
#include <cstdio>
const int maxn = 35;
int dp[maxn][maxn];
int main() {
int n, m;
scanf("%d%d",&n,&m);
dp[0][1] = 1;
for(int i = 1; i <= m; i++) {
dp[i][1] = dp[i - 1][n] + dp[i - 1][2];
dp[i][n] = dp[i - 1][n - 1] + dp[i - 1][1];
for(int j = 2; j <= n - 1; j++)
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
}
printf("%d\n",dp[m][1]);
return 0;
}AC 100:R31341950
标签:输入格式 方法 add 初始 方式 表示 load 多少 png
原文地址:https://www.cnblogs.com/crab-in-the-northeast/p/luogu-p1057.html