标签:矩阵乘法 href 高斯 http 参考 code 其他 ref 逆矩阵
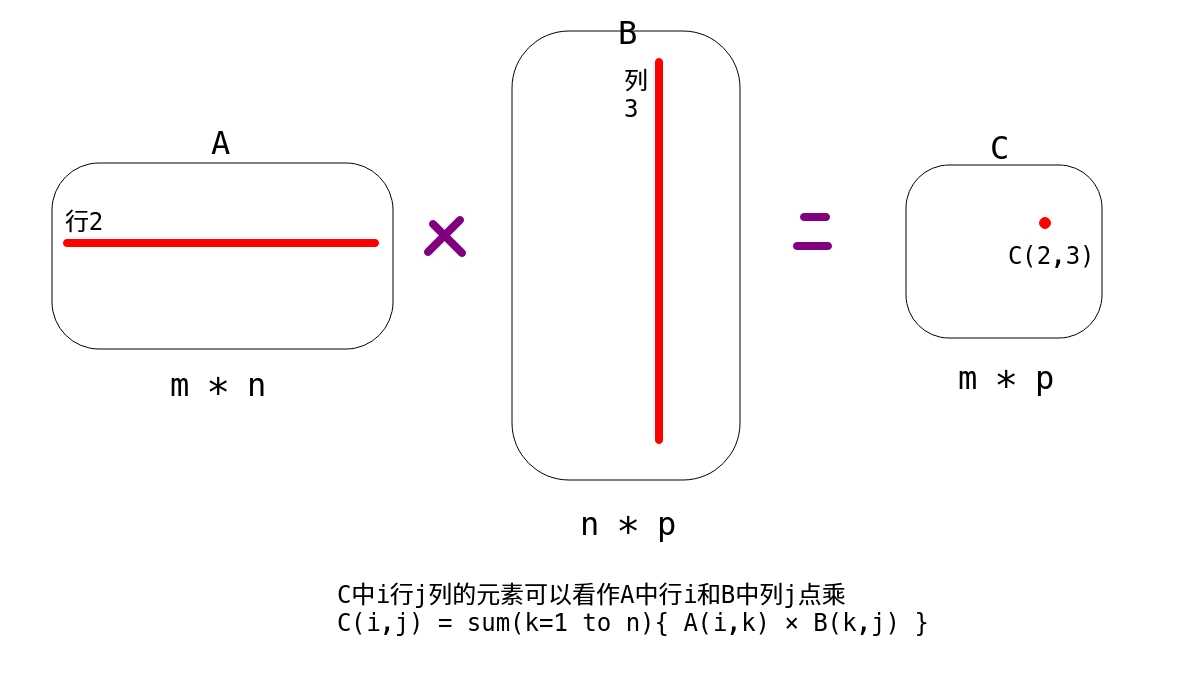
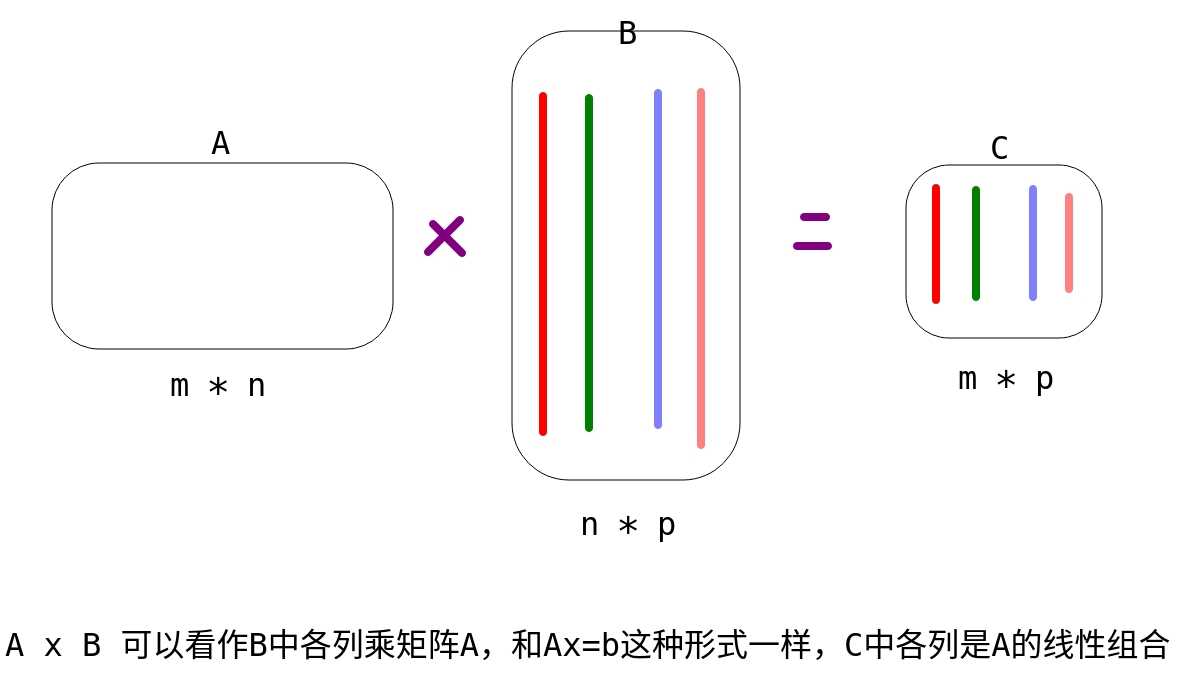
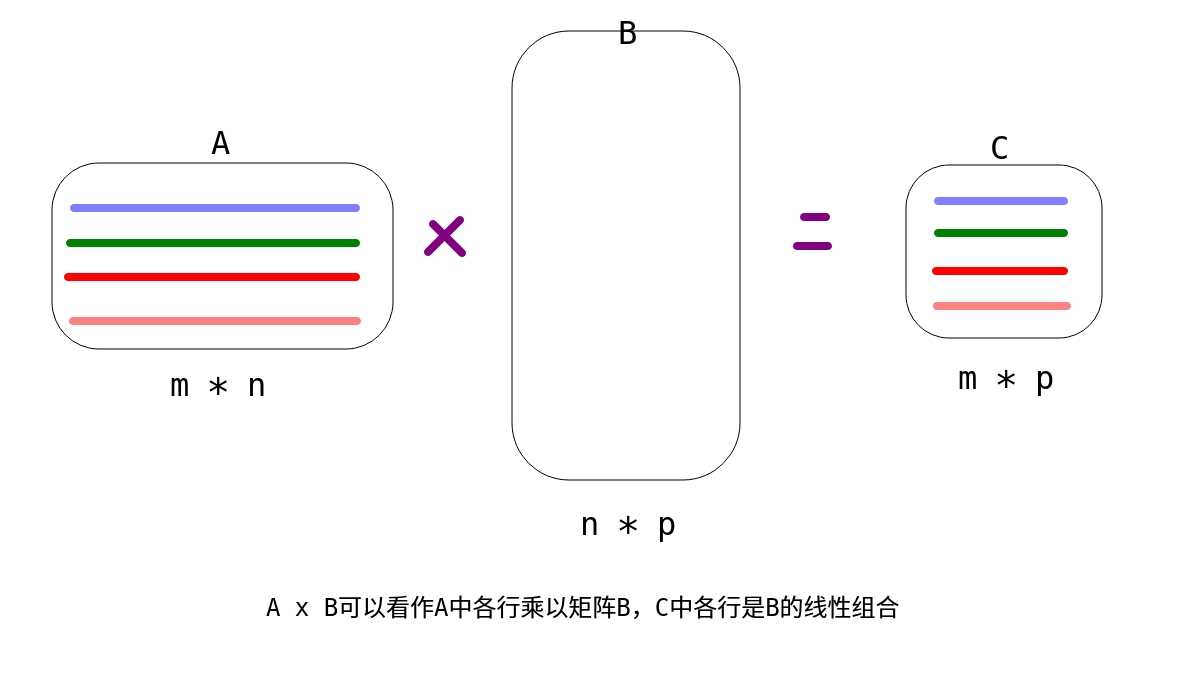
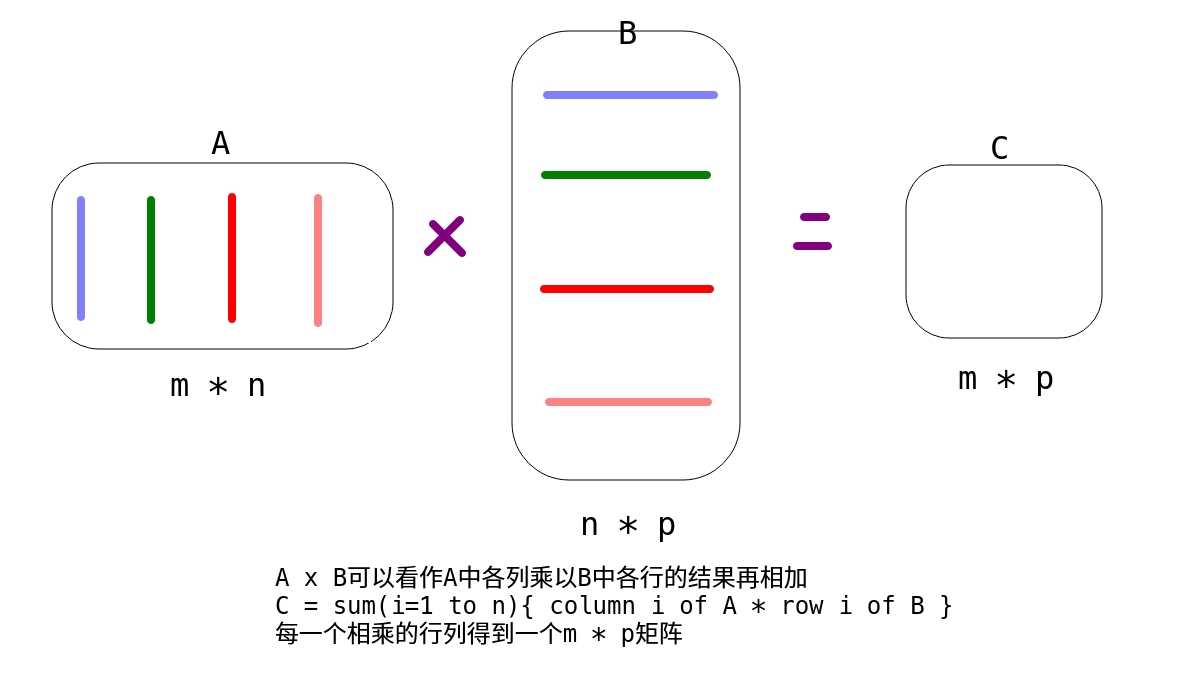
一个矩阵乘以单位矩阵等于本身
\[ \begin{equation} \left[\begin{array}{ccc} 1&2&3\\\4&5&6\\\7&8&9 \end{array} \right] \times{ \left[\begin{array}{ccc} 1&0&0\0&1&0\0&0&1 \end{array} \right]}= \left[\begin{array}{ccc} 1&2&3\4&5&6\7&8&9 \end{array} \right] \end{equation} \]
一个矩阵乘以它的逆矩阵等于单位阵
\[ \begin{equation} A^{-1} \times A = I = A \times A^{-1} \end{equation} \]
如下矩阵无逆
\[ \left[\begin{array}{ccc} 1&3\2&6 \end{array} \right] \]
我们看下原因
第一列向量和第二列向量在一条线上,它们是倍数关系,即使去掉其中一列,矩阵张成的空间也不变。你无论用什么矩阵乘它,得到的都是在这条线上的玩意,而单位阵中的每个向量是不共线的,所以。。。
可以的出结论,如果一个n维方阵不能撑开整个n维空间,他就没有逆。所以下面是矩阵没有逆的条件
\[ \begin{equation} \exists \,vector \,x \,(x \not = 0) \,st. \,Ax=0\存在一个向量x(x不是零向量)使得Ax为零向量 \end{equation} \]
因为有一对下向量是倍数关系,对于这两列我们很容易取一个系数让结果为0,比如上面的例子,第二列是第一列的三倍,我们只需要取3倍的列一和-1倍的列二结果就为0,所以,对于上面的矩阵,x为:
\[ \left[\begin{array}{ccc} 3\-1 \end{array} \right] \]
如果还存在其他不共线的向量直接取0倍即可。
矩阵行列式为0时矩阵没逆
因为有两列共线,消元后就有一个为0的主元,行列式必然是0
假设我们有矩阵A,求解它的逆矩阵,假如那个标满黑人问号的矩阵为所求矩阵,那肯定满足如下公式:
\[ \begin{equation} \left[\begin{array}{ccc} 1&3\2&7 \end{array}\right] \times \left[\begin{array}{ccc} ?&?\?&? \end{array}\right] = \left[\begin{array}{ccc} 1&0\0&1 \end{array}\right] \end{equation} \]
我们线把单位矩阵和A组合起来,变成A的增广矩阵:
\[ \begin{equation} \left[\begin{array}{ccc} 1&3&1&0\2&7&0&1 \end{array}\right] \end{equation} \]
然后对它消元
\[ \begin{equation} 行2减去2倍行1\\left[\begin{array}{ccc} 1&3&1&0\0&1&-2&1 \end{array}\right]\行1减去3倍行2\\left[\begin{array}{ccc} 1&0&7&-3\0&1&-2&1 \end{array}\right]\\end{equation} \]
然后左侧原来的矩阵A变成了单位阵,右侧的就是A的逆矩阵,原理就是我们刻意通过消元找到一个矩阵E乘A为单位阵,因为E在平常的消元步骤中不体现出来,所以把A变成加个单位阵的增广矩阵,E就能体现出来了。
\[ \begin{equation} E\times AI = IE(E=A^{-1}) \end{equation} \]
标签:矩阵乘法 href 高斯 http 参考 code 其他 ref 逆矩阵
原文地址:https://www.cnblogs.com/lilpig/p/12408705.html