322.零钱兑换（动态规划）

标签：leetcode   mamicode   oat   change   官方   转移   算法   sel   tco   

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

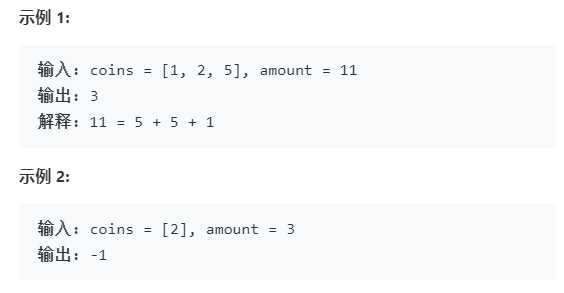
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/coin-change
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

以前我会直接贪婪算法，然后解不出来，现在第一想法就是动态规划：把每一步的最优解都算出来，取最后一项返回。

本题状态转移方程： dp[ i ] =  min(dp[ i - coins[ j ]],......) 

　　特判：1.i - coins[ j ]<0: continue

　　　　    2.if dp[ i - coins[ j ]] == -1: continue  并且 j 对应的dp[ i - coins[ j ]]不加入状态转移方程中的比较，我现在去看看答案。

322.零钱兑换（动态规划）

标签：leetcode   mamicode   oat   change   官方   转移   算法   sel   tco   

原文地址：https://www.cnblogs.com/ChevisZhang/p/12425671.html