标签:序列化 art hot 不同 inf 情感 一般来说 解释 运用
循环神经网络主要运用在序列数据之中,因此下文将以比较典型的文本数据进行分析。
对于神经网络,我们输入的X必须是数字,不然无法参与计算。因此这里就创建一个vocabulary,给每一个词编码。
比如a可能代表1,b可能代表452等;随后我们使用one_hot来代表这些单词。
一般来说,词典的大小,将会成为我们输入的X的维度,因此循环神经网络的计算量往往很大。
为了充分利用序列化数据的序列特征,循环神经网络将X的每一个单位数据称为一个时间步的数据。这里以《动手学深度学习》一书中的插图进行分析。
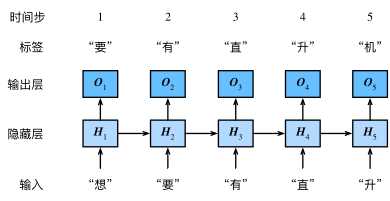
从图中可以看出,时间步,输入,隐藏层,输出,标签等;
这里的输入就是我们的词向量,通过隐藏层,来预测一个我们想要的结果。图中的预测结果即是下一个时间步的标签,但事实上,输出的结果完全可以由我们自己决定。当然这也取决于模型的使用目的。
一般来说,循环神经网络中的输入和输出是相同的,就像图中一样。但是也有不少循环神经网络输入输出的数量并不同。常见的如情感分析,只需要在循环神经网络最后一步输出一个结果。
现在进入数学部分。
$\boldsymbol{H}_{t}=\phi\left(\boldsymbol{X}_{t} \boldsymbol{W}_{x h}+\boldsymbol{H}_{t-1} \boldsymbol{W}_{h h}+\boldsymbol{b}_{h}\right)$
这一步是关于H的计算,H的计算主要考虑前一步的隐藏层输出以及这一步的输入,即Ht-1和Xt。
在隐藏层中,常用的激活函数是tanh。
$\boldsymbol{O}_{t}=\boldsymbol{H}_{t} \boldsymbol{W}_{h q}+\boldsymbol{b}_{q}$
这里是每一步的输出层输出的计算,它将隐藏层的输出作为输入进行线性计算。
反向传播的过程稍微复杂,这主要是由于循环神经网络在计算的过程中,涉及不同箭头的计算。
$a^{(t)}=\tanh \left(W_{a x} x^{(t)}+W_{a a} a^{(t-1)}+b\right)$
$\frac{\partial \tanh (x)}{\partial x}=1-\tanh (x)^{2}$
$\frac{\partial a^{(t)}}{\partial W_{a x}}=\left(1-\tanh \left(W_{a x} x^{(t)}+W_{a a} a^{(t-1)}+b\right)^{2}\right) x^{(t) T}$
$\frac{\partial a^{(t)}}{\partial W_{a a}}=\left(1-\tanh \left(W_{a x} x^{(t)}+W_{a a} a^{(t-1)}+b\right)^{2}\right) a^{\langle t-1\rangle T}$
$\frac{\partial a^{(t)}}{\partial b}=\sum_{\text {buch}}\left(1-\tanh \left(W_{a x} x^{\langle t\rangle}+W_{a a} a^{\langle t-1\rangle}+b\right)^{2}\right)$
$\frac{\partial a^{(t)}}{\partial x^{(t)}}=W_{a x}^{T} \cdot\left(1-\tanh \left(W_{a x} x^{(t)}+W_{a a} a^{(t-1)}+b\right)^{2}\right)$
$\frac{\partial a^{(t)}}{\partial a^{(t-1)}}=W_{a a}^{T} \cdot\left(1-\tanh \left(W_{a x} x^{(t-1)}+W_{a a} a^{(t-1)}+b\right)^{2}\right)$
反向传播的方向就是把前向传播的箭头全部改变方向,这里不做一一解释。
标签:序列化 art hot 不同 inf 情感 一般来说 解释 运用
原文地址:https://www.cnblogs.com/siyuan-Jin/p/12427113.html