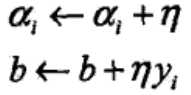感知机属于有监督的学习，生成的模型称为判别模型。其通过特定的函数将输入的特征向量，输出为实例的类别（+1或-1），该函数即为将实例划分为两类的分离超平面。为获得最优化的超平面，感知机引入了基于误分类的损失函数。感知机是神经网络和支持向量机的基础。

 

有监督学习分为生成模型和判别模型两种。其分别含义如下：

(1)生成模型：通过输入数据学习联合概率分布P(X,Y)得到的条件概率分布P(Y|X)作为预测模型；

(2)判别模型：通过输入数据直接学习得到的决策函数f(x)或条件概率分布P(Y|X)作为预测模型。

 

1.perceptron 定义

在特征空间中，感知机由输入空间到输出空间的函数为

 f(x)=sign(w · x + b)

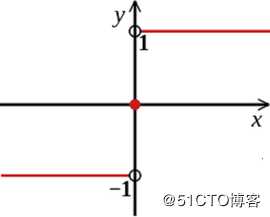
其中，参数w叫做权值向量，b称为偏置。w·x表示w和x的内积。sign为符号函数，即

技术图片

2. perceptron的几何意义

    感知机模型是线性分类模型，其线性方程 w·x+b=0 对应于特征空间Rn中的一个超平面S（可以同时存在多个超平面），超平面将特征空间分成两部分，位于两侧的点分别为正负两类。其中w是超平面的法向量，b是超平面的截距。

技术图片

3. perceptron 策略

    感知机的数据集必须是线性可分的，即存在至少一个超平面可以把数据完全正确的划分到两边，进而得到参数w和b的值。为此需要确定一个（经验）损失函数，并将该损失函数最小化。

    损失函数我们可以考虑误分类的总数，但是这样得到的损失函数不是参数w、b的连续可导函数，不宜优化。因此我们选择以误分类点到超平面的距离之和作为损失函数。最终得到损失函数定义为：

 

技术图片

 

超平面S的总的误分类点集合为M。其中，空间中任意一点到超平面的距离为（||w||是w的L2范数）：

技术图片

4.perceptron 算法

    感知机学习其实就是损失函数最小化的过程。任意选取一个超平面，采用梯度下降法不断逼近最小损失函数。逼近过程中并不是一次使用误分类集合中所有点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

(1) 原始形式

实现过程：

输入：训练数据集T={(x1,y1),(x2,y2),(x3,y3),...,(xn,yn)}、学习率η(0 < η ≤ 1)

输出：感知机模型f(x)=sign(w · x + b)

①选择初始值w0,b0
②在训练集中选取数据(xi,yi)
③如果yi(w ·xi+b)≤0

技术图片

④跳转至②，直至训练集中没有误分类点

算法解释：当前存在某个点被误分类时，则调整w，b的值，使分离超平面向该点一侧运动，直到该点被超平面正确分类为止。

#--*-- coding:utf-8 --*--
#初始化相关参数
w = [0, 0]
b = 0
setp = 0

#参数调整
def adjust(item, study_r=1): #学习率初始化为1
    global w, b, setp
    for i in range(len(item[0])):
        w[i] += study_r * item[1] * item[0][i]
    b += item[1]
    setp += 1

def mis_value(item):
    #误分类值计算，该值小于等于时表示当前存在误分类点
    value = 0
    for i in range(len(item[0])):
        value += item[0][i] * w[i]
    value += b
    value *= item[1]
    return value

def decide(datas):
    flag = False
    for item in datas:
        mis = mis_value(item)
        if mis <= 0:
            flag = True
            adjust(item)
            print setp, item, w, b,mis
    if not flag:
        print setp+1, item, w, b,mis
        print "\n最终得到超平面相关参数：\n w= " + str(w) + ",  b=" + str(b)
    return flag

if __name__ == "__main__":
    training_set = [[(3, 3), 1], [(4, 3), 1], [(1, 1), -1]]  #以书本中的数据集为例
    print ‘迭代次数‘, ‘误分类值‘, ‘权值w‘, ‘截距b‘, ‘判断值‘
    while decide(training_set):
        continue

　　

执行结果为：

迭代次数 误分类值 权值w 截距b 判断值
1 [(3, 3), 1] [3, 3] 1 0
2 [(1, 1), -1] [2, 2] 0 -7
3 [(1, 1), -1] [1, 1] -1 -4
4 [(1, 1), -1] [0, 0] -2 -1
5 [(3, 3), 1] [3, 3] -1 -2
6 [(1, 1), -1] [2, 2] -2 -5
7 [(1, 1), -1] [1, 1] -3 -2
8 [(1, 1), -1] [1, 1] -3 1

最终得到超平面相关参数：
 w= [1, 1],  b=-3
 

(2)对偶形式

实现过程：

输入：训练数据集T={(x1,y1),(x2,y2),(x3,y3),...,(xn,yn)}、学习率η(0 < η ≤ 1)

输出：α,b；感知机模型:

技术图片

技术图片

 

①α←0,b←0
②在训练集中选取数据(xi,yi)
③如果技术图片

技术图片

④跳转至②，直至训练集中没有误分类点

算法解释：当前存在某个点被误分类时，则调整，b的值，使分离超平面向该点一侧运动，直到该点被超平面正确分类为止。

    由于对偶形式各训练实例是以内积的形式存在，因此可以预先计算出实例间的内积，该结果以矩阵的方式存储，即Gram矩阵(Geam matrix)。

 

#--*-- coding:utf-8 --*--
from numpy import *
setp = 0
b = 0

#获取Gram矩阵
def gram_matrix(datas):
    gm = ones((len(datas), len(datas)), int) #生成全为1的多维数组
    for i in range(len(datas)):
        for j in range(len(datas)):
            gm[i][j] = dot(datas[i][0], datas[j][0])
    return gm

#参数调整
def adjust(i, study_r=1): #学习率初始化为1
    global alpha, b, setp
    alpha[i] += study_r
    b = b + y[i]
    setp += 1

#误分类值计算，该值小于等于时表示当前存在误分类点
def mis_value(i):
    global alpha, b, x, y
    value = dot(alpha * y, Gram[i])
    value = (value + b) * y[i]
    return value

def decide(datas):
    global alpha, b, x, y
    flag = False
    for i in range(len(datas)):
        mis = mis_value(i)
        if mis <= 0:
            flag = True
            adjust(i)
            print setp, alpha[0], alpha[1], alpha[2], b, mis
    if not flag:
        print setp+1, alpha[0], alpha[1], alpha[2], b, mis
        w = dot(alpha * y, x)   #alpha转化为w
        print "\n最终得到超平面相关参数：\n a1=" + str(alpha[0]) + " a2=" + str(alpha[1]) + " a3=" + str(alpha[2]) + " b=" + str(b),             "\n转化后相关参数为：\n w= " + str(w) + ",  b=" + str(b)
        return False
    return True


if __name__ == "__main__":
    training_set = array([[(3, 3), 1], [(4, 3), 1], [(1, 1), -1]])
    alpha = zeros(len(training_set),int)
    Gram = None
    y = array(training_set[:, 1],int)
    x = ones((len(training_set), 2),int)
    for i in range(len(training_set)):
        x[i] = training_set[i][0]
        Gram = gram_matrix(training_set)
    print ‘迭代次数‘, ‘a1‘, ‘a2‘, ‘a3‘, ‘截距b‘, ‘判断值‘
    while decide(training_set):
        continue
 

执行结果为：

迭代次数 a1 a2 a3 截距b 判断值
1 1 0 0 1 0
2 1 0 1 0 -7
3 1 0 2 -1 -4
4 1 0 3 -2 -1
5 2 0 3 -1 -2
6 2 0 4 -2 -5
7 2 0 5 -3 -2
8 2 0 5 -3 1

最终得到超平面相关参数：
 a1=2 a2=0 a3=5 b=-3 
转化后相关参数为：
 w= [1 1],  b=-3

 

 

reference:《统计学习学习方法》

 原文转发，转自：https://blog.51cto.com/abezoo/1943592