标签:定义 最简 百度 必须 主表 strong 注意 回收 while
说起这个问题,我们一定不陌生。打开QQ或微信,我们可以看到好友列表,打开PTA,我们能看到题目列表,打开音乐软件,我们可以看见歌曲列表,线性表在我们的生活中无处不在。线性表是怎么呈现的呢?线性表把我们在生活中需要的信息,按照顺序进行排列,使得这些信息直观、有条理,如果是按照某种顺序排列的列表,我们可以做到信息的快速检索。
在数据结构中,线性表是最基本、最简单、也是最常用的一种数据结构。所谓线性表,是零个或多个数据元素的有限序列,线性表的元素具有相同的特征,数据元素之间的关系是一对一的关系。用数学语言来描述线性表,用n表示链表的长度,设序列中第i个元素(a1,…,ai-1,ai,ai+1,…,an),当表的长度为0时,就表示这是一个空表。那么线性表的一个数据元素包含多少数据项呢?就好比学生学籍信息表,除了学生的姓名,还会有诸如学号、出生日期、户籍所在地等信息,因此线性表的一个数据元素可以由多个数据项组成。如图所示:

ADT List
{
Data:
D = {ai | 1 ≤ i ≤ n, n ≥ 0, ai 为 ElemType 类型}
Relation:
R = { <ai,ai+1> | ai,ai+1 ∈ D, i = 1, i ∈ (0,n)}
Operation:
InitList(&L); //初始化,建立一个空的线性表L
MakeList(&L); //建立线性表,向表中存入数据
ListEmpty(*L); //空表判断,是则返回true,否则返回false
DestroyList(&L); //清除操作,清空线性表的元素
GetElem(L,i,&e); //获取线性表的元素,将线性表L的第i个元素的值返回给e
LocateElem(L,e); //按值查找元素,在线性表L中查找与e元素相等的元素,查找成功返回对应的序号,查找失败则返回0
ListInsert(&L,i,e); //插入操作,在线性表L的第i个位置插入元素e
ListDelete(&L,i,&e); //删除操作,删除线性表L中的第i个位置的元素,并将其用e返回
ListLength(L); //计算表长,返回线性表L的元素个数
DispList(L); //输出线性表,当线性表不为空表时,按顺序输出表中的每一个元素
}例如你有两个线性表分别是L1、L2,现在你要做的事情是合并两个表,即实现L1∪L2操作。思路很自然,我们直接去遍历L2,然后判断一下L2的元素是否是L1未包含的,如果是就将该元素插入L1即可。
代码实现:
void unionList(List &L1,List L2)
{
int len_a,len_b;
int i;
ElemType e;
len_a = ListLength(L1); //获取表长
len_b = ListLength(L2);
for (i = 1; i <= len_b; i++)
{
GetElem(L2,i,e); //获取线性表L2中的第i个元素
if(!LocatElem(L1,e)) //判断元素e是否已经包含于线性表L1
{
ListInsert(La, ++len_a, e); //若还未包含,执行插入插入
}
}
}由此我们就能够明白了,一个复杂的操作,离不开对基本操作的组合应用。
线性表的顺序存储结构是,把线性表中的所有元素按照其逻辑顺序依次存储到从计算机存储器中指定存储位置开始的一块连续的存储空间中,线性表中逻辑上相邻的两个元素在对应的顺序表中的存储位置也相邻。在C/C++中,我们使用一维数组实现线性表的顺序存储结构,当我们定义了一个数组,就分配了一块连续的存储空间,该存储空间的起始位置就是由数组名表示的地址常量,数组的基本类型就是线性表中元素的类型,需要注意的是数组的大小要大于等于线性表的长度。
在用代码描述线性表的顺序存储结构时,我们先要定义一个整型常量 MAXSIZE,用来表示线性表最大数据元素容纳量。由于我们创建的线性表是动态的,即我们需要经常向表中修改、插入和删除元素,因此需要有一个变量 Last 来存储线性表最后一个元素的位置,即表的实际长度,为了继承这些要素,我们用结构体类型来表示:
#define MAXSIZE 50
typedef int Position;
typedef int ElementType; //int可改为其他数据类型
typedef struct SqList *List;
typedef struct
{
ElementType Data[MAXSIZE]; //存放线性表中的元素
Position Last; //保存线性表中最后一个元素的位置,表示表长
}SqList; //线性表类型定义线性表的第一个元素,即下标为0的元素,是存储在这个数组的起始位置,假设存储地址是 LOC(A)。则第二个元素存储于下标为1的位置上,那么存储位置是“LOC(A)+1”吗?并不是,线性表中的每个元素都需要提供一定的空间来存储,单个元素所占的空间大小因类型的不同而不同,因此第二个元素的地址是 LOC(A) + sizeof(ElemType)。
以此类推,第i个元素的地址为:
LOC(Ai) = LOC(A) + sizeof(ElemType) * (i - 1)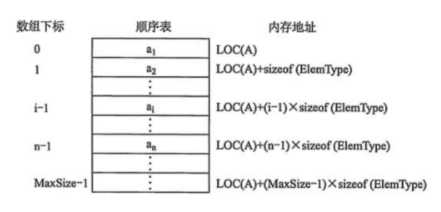
初始化顺序表的目的是构造一个空的顺序表L,我们需要分配足够的存储空间,并将表长设置为0。
List InitList()
{
List L;
L = new SqList; //分配存放顺序表的空间
L->Last = 0;
return L;
}将给定含有n个元素,将n个元素依次输入,并放入到顺序表中,并将n赋值给顺序表的变量 Position。
void MakeList(List &L)
{
int i;
cin >> n;
for(i = 0; i < n; i++)
{
cin >> L->Data[i]; //输入数据
}
L->Last = n; //设置表长
}直接将顺序表L的空间释放掉。
void DestroyList(List &L)
{
delete L;
}利用顺序查找查找第一个与e相等的元素返回线性表中e的位置,若找不到则返回值为-1。
Position LocateElem(List L, ElementType e)
{
int i = 0;
for (Position i = 0; i <= L->Last; i++)
{
if (L->Data[i] == e)
{
return i;
}
}
return 0;
}将e插入在位置P并返回true,若空间已满或参数P指向非法位置并返回false,插入时我们需要从最后一个元素开始,遍历到第i个元素,并将这些元素都往后移动一个位置,以便于给需要插入的元素提供足够的空间。
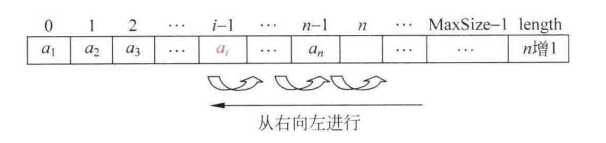
bool Insert(List L, ElementType e, Position P)
{
int i;
if (L->Last + 1 >= MAXSIZE) //判断空间是否已满
{
return false;
}
if (P > (L->Last + 1) || P < 0) //参数错误时返回false
{
return false;
}
for (i = L->Last; i >= P; i--) //将data[P]及后面元素后移一个位置
{
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X; //插入数据
L->Last += 1; //顺序表长度加1
return true;
}将位置P的元素删除并返回true,若参数P指向非法位置,则返回false,删除元素后,我们需要从删除的位置开始遍历到最后一个位置,并将它们往前移动一个位置。
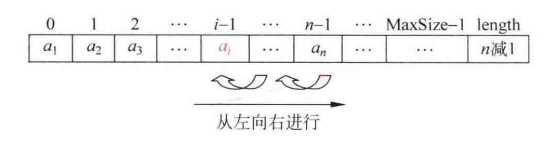
bool Delete(List L, Position P)
{
int i;
if (P > L->Last || P < 0)
{
return false; //参数错误返回 false
}
for (i = P; i < L->Last; i++)
{
L->Data[i] = L->Data[i + 1]; //将data[P]之后的元素向前移动一个位置
}
L->Last -= 1; //顺序表长度减1
return true;
}首先是插入操作,插入操作时间复杂度最小的情况是,当元素要插入到最后一个位置时,你就不需要移动任何元素即可实现,只需要将需要插入的元素插在表的末端即可,时间复杂度O(1),最费时的操作就是插入的元素要放在表头,那我们就需要把表中的所有元素都移动了,时间复杂度为O(n)。删除操作也如此,当我们要删除最后一个元素,也不需要移动顺序表,而删除第一个元素时需要移动整个表。我们知道,在实际的操作中,删除表中的任何一个位置需要被插入删除的可能性是相同的,因此从平均角度来分析,移动表的平均次数为 (n - 1) / 2,时间复杂度为O(n)。
因此我们可以看出,顺序表在插入、删除操作时是比较费时间的,然而其他的基本操作例如初始化、建表或者销毁,时间复杂度都是O(1),因此我们在使用顺序表的时候,要尽量让表保持不变,而是多多使用顺序表的存储和随机提取等优点。
我们在实际应用中,也往往会很喜欢去使用顺序表,因为顺序表的操作是很便捷的,但是我们一直对顺序表,或者说数组在定义的时候需要给的具体长度这个问题很头疼。我们想到的问题,开发者也想到了,那么现在我们有什么方式可以消除这个问题的限制?C语言是怎么解决的?C++又是怎么解决的?

根据上文的分析,我们就明白了插入、删除操作对于顺序表来说,时间复杂度是较大的,当我们需要一张不断在发生变化的线性表时,顺序表就显得很不合适。这是因为在我们定义一个数组的时候,元素之间的逻辑关系是不需要另附代码描述,这就导致了要修改元素的次序就变得不那么容易。而数组在存储方面,各个元素的存储位置是一个连续的空间,这就导致了我们如果想要插入元素时,需要插入的位置是没有多余的空间来插入的,所以我们只好通过移动其他元素来腾出空间。
首先是存储空间的问题,我们希望我要存储多少数据,就申请多少空间,这种申请是动态的,第二是各个元素之间的逻辑描述,我们希望这种逻辑描述是可变的,以便于我们能直接添加或删除元素,而不是牵一发而动全身。综合这两种思考,我们引入了线性表链式存储结构。
线性表的链式存储结构,是利用一组任意的存储单元存储线性表的数据元素,这些存储单元可以是非连续的,因此它们可以存在于内存的不同且可用的地方。由于这些元素的位置不连续,因此为了使一个元素能够在逻辑上找到下一个元素,我们需要额外设置变量来描述这个关系。在C/C++中我们有指针可以来实现,通过指针来连接逻辑上连续的结点,因此每个结点的存储位置不一定需要连续。每个存储结点都配备数据域和指针域,数据域用于存储数据,指针域用于存放一个指向下一个元素的指针,使得各个元素之间在逻辑上成为一个表结构,这样可以通过一个结点的指针域方便地找到后继结点的位置。每个结点有一个或多个这样的指针域,有多个指针域时,就可以描述更复杂的逻辑结构,若一个结点中的某个指针域不需要指向其他任何结点,则需要将它的值置为空,用常量NULL表示。

在单链表中.由于每个结点只包含有一个指向后继结点的指针,因此当访问过一个结点后,只能接着访问它的后继结点。

我们来写一个单链表的结点类型 LinkList:
typedf struct LNode //定义单链表结点类型
{
ElemType data; //数据域,存放数据
struct LNode *next; //指针域,指向后继结点
}LinkList,*List;链表的第一个结点的存储位置成为头指针,链表的读取从头指针开始。头指针顾名思义是起到表头的作用,通常头指针的名称就是一个链表的名称,由于其重要的地位,它不能为 NULL。
为了操作更方便,我们一般会给链表设置一个头结点。头结点放在线性表第一个元素的前面,指针域指向该元素,头结点的数据域可以是无意义的,也可以做一些其他操作,例如存储表长。通过头结点,我们对表的第一个元素的插入删除结点变得容易,但是头结点并非必要元素,当头结点存在时,指向头结点的指针为头指针。下文所建立的链表都是带头结点的链表。
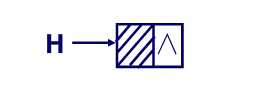
头插法建立的链表,表中元素顺序与输入时相反,新结点插入位置是表头。
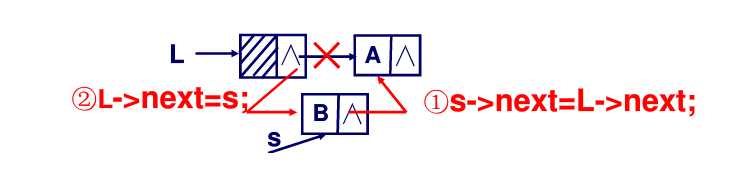
void CreateListF(LinkList& L, int n)
{
LinkList head, ptr;
head = new(LNode); //创建头结点
head->next = NULL; //初始化头结点的后继为NULL
for (int i = 0; i < n; i++)
{
ptr = new(LNode); //创建新结点
cin >> ptr->data;
ptr->next = head->next; //连接表身
head->next = ptr; //将新结点插到表头
}
L = head;
}尾插法建立的链表与数据的输入次序相同,建立链表时,新结点被插入链表的表尾上,此时需要一个尾指针用于指向表尾。
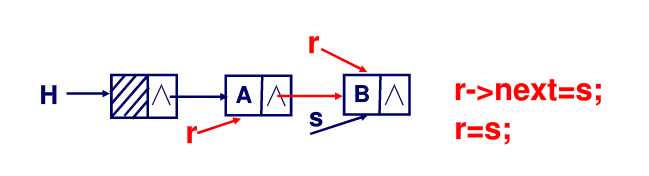
void CreateListR(LinkList& L, int n)
{
LinkList ptr, head, tail;
head = new LNode; //创建头结点
tail = head; //尾结点指向表尾,初始化为头结点
head->next = NULL; //头结点的后继初始化为NULL
for (int i = 0; i < n; i++)
{
ptr = new LNode; //创建新结点
cin >> ptr->data
ptr->next = NULL;
tail->next = ptr; //新结点插在表尾
tail = ptr; //更新表尾
}
L = head;
}要在位置i插入一个新结点,我们需要先找到第i-1个结点的位置,这就需要从头结点遍历到第i-1个结点的位置,然后申请一个新结点,令新结点的后继为原来第i-1个结点的后继,令第i-1个结点的后继为新结点。
s = new LNode;
s->next = pre->next
pre->next = s;完整代码,将X插入在位置P指向的结点之前,返回true。如果参数P指向非法位置,则返回false:
bool Insert(List L, ElementType X, Position P)
{
List head = L, ptr;
ptr = new LNode;
ptr->Data = X;
while (L != NULL)
{
if (L->Next == P)
{
ptr->Next = L->Next; //将新结点的后继连接到后续结点
L->Next = ptr; //插入新结点
return true;
}
L = L->Next; //移动结点直到i-1位置
}
return false;
}需要注意的是,上述操作的顺序不能对调,否则原链表的逻辑关系会被切断,后续的元素无法被连接。
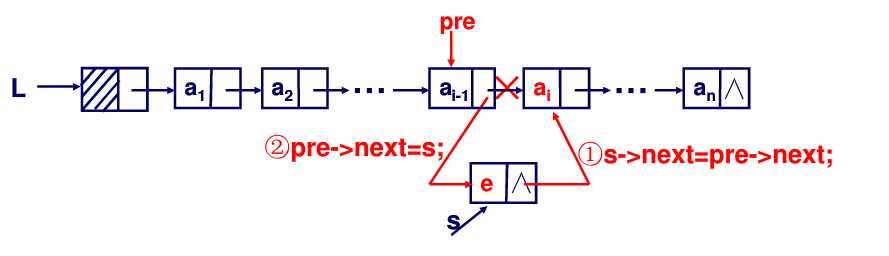
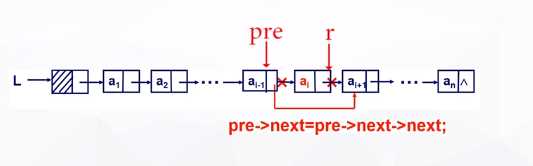
删除第i个结点时,我们同样需要找到第i-1个结点,再删除其后的结点。删除操作时,我们需要先拷贝一份被删除的结点,然后修改第i-1个结点的指针域,使其指向下一个结点的后继。删除操作之后,我们需要把被删除的结点的空间释放掉,以免出现内存碎片。
ptr = pre->next;
pre->next = pre->next->next;
delete ptr;完整代码,将位置P的元素删除并返回true。若参数P指向非法位置,则返回false:
bool Delete(List L, Position P)
{
List head = L, ptr;
while (L->Next != NULL)
{
if (L->Next == P)
{
ptr = L->Next; //拷贝要删除的结点
L->Next = L->Next->Next; //连接后续结点
delete ptr; //释放空间
return true;
}
L = L->Next; //移动结点直到P位置之前
}
return false;
}
初始化链表是,只需要建立一个头结点即可。
List MakeEmpty()
{
List head;
head = new LNode; //为头结点申请空间
head->Next = NULL; //头结点的后继初始化为NULL
return head;
}销毁链表本质上是重复的删除结点操作,从头结点开始依次将每个结点的空间释放。
void DestroyList(LinkList &L)
{
LinkList ptr = L;
while (L != NULL) //遍历单链表
{
ptr = L; //拷贝结点
L = L->next;
delete ptr; //释放单个结点的空间
}
}若线性表L没有后继结点,返回true,否则返回false。
bool ListEmpty(LinkList *L)
{
return (L->next == NULL);
}遍历链表直到表尾,返回结点个数。
int Length(LinkList L)
{
int length = 0;
while (L->next != NULL)
{
length++;
L = L->next;
}
return length;
}顾名思义,就是有序的线性表,表中的所有元素都以递增或递减的形式有序排列。它本是上还是线性表,因此对于线性表的所有操作都可以应用于有序表,我们需要关注的是有序表的插入操作以及归并操作。有序表是线性表的一个基础的应用,同时我们也可以通过这种应用去体会顺序表和链表的特点与不同之处。下列代码是在元素顺序为升序的有序表中的操作。
执行插入操作时,我们并不关注元素 e 插入的位置,需要关注的是我要怎么操作才能保证操作结束后,L 仍然是个有序表。
void LinkInsert(SqList &L, ElemType e)
{
int i = 0,j;
while(i < L->Length && L->data[i] < e)
{
i++; //定位元素 e 插入的位置。
}
for(j = ListLength(L); j > i; j--)
{
L->data[j] = L->data[j - 1]; //将插入位置后面的元素后移1位
}
L->data[i] = e;
L->Length++; //表长加1
}void ListInsert(List &L,ElemType e)
{
List *pre = L, *ptr;
while(pre->next != NULL && e > pre->next->data)
{
pre = pre->next; //找到插入位置的前驱结点
}
ptr = new LNode; //申请空间作为新结点
ptr->data = e;
ptr->next = pre->next; //插入操作
pre->next = ptr;
}
要归并两个有序表,相比归并两个无顺序要求的线性表要复杂一些,因为有序表需要时刻保证表中的数据是有序的。执行归并操作的时候,我们要采用动态操作的思想,同时遍历两张表,同时移动下标或指针,遇到较小的元素就归并到新表上。
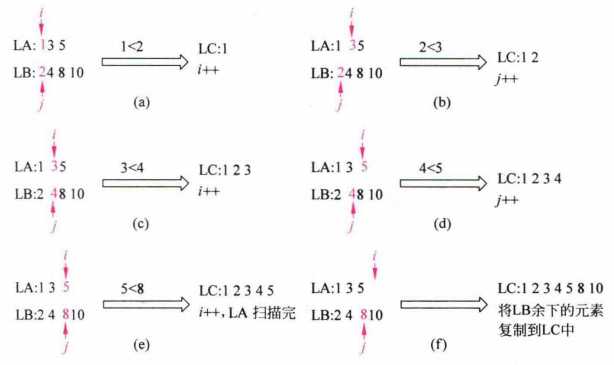
操作的目的是把有序顺序表 LA, LB 的元素归并到新表 LC 上,我们需要同时遍历 LA 和 LB,将元素依次拷贝到 LC 上。
void UnionList(SqList *LA, SqList *LB, SqList &LC)
{
int i = 0, j = 0, k = 0; //由于需要动态操作3个表,因此需要3个变量操作下标
LC = new SqList; //为新表LC申请空间
while(i < LA->Length && j < LB-> Length) //同时遍历两张表,将元素归并到 LC 上
{
if(LA->data[i] < LB->data[j])
{
LC->data[k++] = LA->data[i++];
}
else
{
LC->data[k++] = LB->data[j++];
}
}
while (i < LA->Length) //处理 LA 剩余的元素
{
LC->data[k++] = LA->data[i++];
}
while (i < LB->Length) //处理 LB 剩余的元素
{
LC->data[k++] = LB->data[j++];
}
LC->Length = k;
}写单链表归并时,我们换一种思路来,顺序表我们为了便于操作,将两个有序表的元素拷贝到新表上,而链表我们用转移的思想去实现,因为链表的元素为结点,结点的插入和删除是一件容易的事情,所以我们的想法是把 L2 中的结点依次转移到 L1 中,就不需要再申请新的空间了。
void UnionList(List& L1, List &L2)
{
LinkList ptr, head = L1;
while (L1->next != NULL && L2->next != NULL)
{
if (L1->next->data == L2->next->data)
{
L2 = L2->next;
}
else if (L1->next->data > L2->next->data)
{
ptr = L2->next;
L2->next = L2->next->next;
ptr->next = L1->next;
L1->next = ptr;
}
L1 = L1->next;
}
if (L2->next != NULL)
{
L1->next = L2->next;
}
L1 = head;
}不支持随机读取,要使用链表的单个元素,必须从第一个开始遍历。
其实我们每次用链表来做事情,都觉的挺累的,因为我们建链表需要写一段代码,输出链表元素需要一段代码,获取表长、插入删除结点都需要一波操作才能实现,我们一直在为一些必要的操作投入时间。我们想到的问题,开发者也想到了,我们希望更便利于利用链式存储结构来解决问题,优化代码效率,提高代码的正确性,那么C++要怎么实现我们的愿望呢?

据说著名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决?Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。————百度百科

这个故事还有其他的描述,例如猴子选大王、报数问题等等,这故事也产生了一个著名的算法————约瑟夫算法。我们曾经是怎么解决这个问题的?可能是开一个一维数组,用数组的下标表示人或猴子的序号,然后开始报数操作,出局的序号对应的数组单元改成另一个值,如果遇到已经出局的下标就跳过,跑到数组的上限就复位到第一个单元上,直到剩下最后一个下标。要描述我们以前的做法还是很麻烦的,其中一个最头疼的地方就是如果报数报到了数组的上限,那我们还得敲几行代码手动复位,好麻烦啊,有没有一种结构可以在我们跑到结构的最底端时,能够帮我们轻松地回到结构的顶端呢?
当我们建一条单链表的时候,头结点的后继会先被我们初始化为 NULL,无论我们使用头插法还是尾插法建链表,建好的表的最后一个结点的指针域也会是 NULL,一次表示链表的表尾。我们能不能把这个指针利用起来,实现复位到表头的操作呢?答案是显然的、我们可以将单链表的最后一个结点的指针域由 NULL 修改为指向头结点,在经过这样的操作之后,这个单链表就会形成一个环结构,这种头尾相接的单链表就是循环链表。
制作一个循环表,令我们无论从哪个结点开始遍历,都能遍历到所有的结点,不过为了让我们能够找到表头,我们还是需要头结点这个好东西,使用循环表能够是一些功能的实现变得简单。
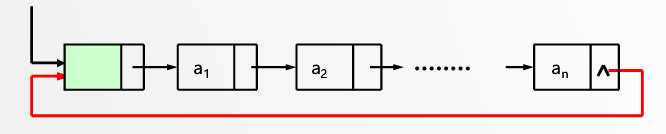
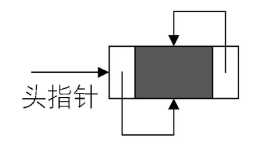
与初始化单链表类似,不过我们得把头结点的后继指向它本身,如图所示:
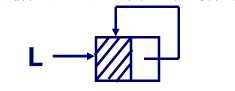
代码实现:
List MakeEmpty()
{
List head;
head = new LNode; //为头结点申请空间
head->Next = head; //头结点的后继初始化为头结点
return head;
}在单链表中,我们的苦恼还有很多,例如我有一个已经建好的单链表,这时我要在链表的表尾添加新数据,我就必须从头结点开始遍历一遍链表,知道表尾,这么干的时间复杂度为 O(n)。当我们在写程序的时候,我们总是喜欢思考如何让算法更快,例如我有一个时间复杂度为 O(n) 的算法,我们能不能让它更快,时间复杂度降到 O(㏒n) 甚至更快呢?
在循环表中,使用尾指针让我们能够轻松地访问表尾,顾名思义,“尾指针”就是要指向表尾的。那么表头怎么办呢?别忘了,我们现在建的是循环表,那么表尾结点的后继就是头结点,表尾结点的后继的后继就是表头结点,也就是说在循环表中尾指针不仅可以指向尾结点,还可以通过尾结点达到访问头结点的目的。
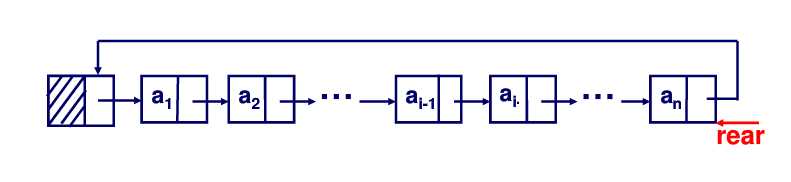
合并循环链表并不是一件很复杂的事情,与合并两个单链表操作类似,先找到第一个表的尾结点,令其的后继为第二个表的表头结点。对于循环表,我们还得多做一步,将第二个表的表尾结点的后继修改为第一个表的头结点,也就是说我们得花点时间找到第二个表的尾结点,时间复杂度为 O(n)。
不过,当我们有了尾指针,合并循环表的操作将变得更为简单,而且时间复杂度为 O(1)。
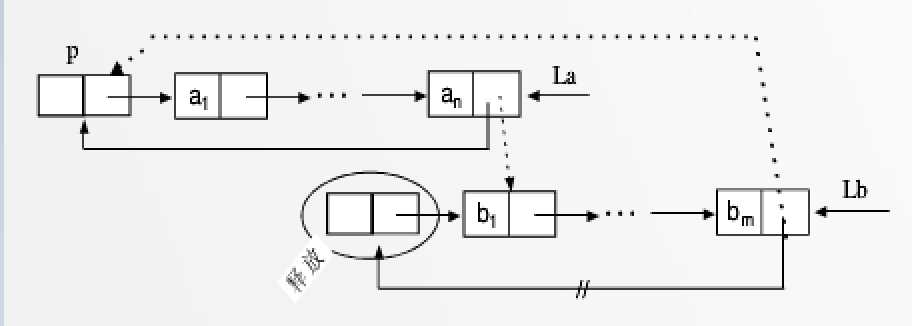
Link MergeLink(Link list1_tail, Link list2_tail)
{
LNode *ptr;
ptr = list1_tail->next; //保存 list1 的头结点
list1_tail->next = list2_tail->next->next; //将 list1 的后继修改为 list2 的表头结点
delete list2_tail->next; //释放 list2 的头结点
list2_tail->next = ptr; //修改 list2 尾结点的后继为 list1 的头结点
return list2_tail; //返回合并后的头结点
}问题的情景是:有 n 个人围成一圈,按顺序从1到 n 编好号,从第一个人开始报数,报到 m(<n)的人退出圈子,下一个人从1开始报数,报到 m 的人退出圈子,如此下去,直到留下最后一个人。
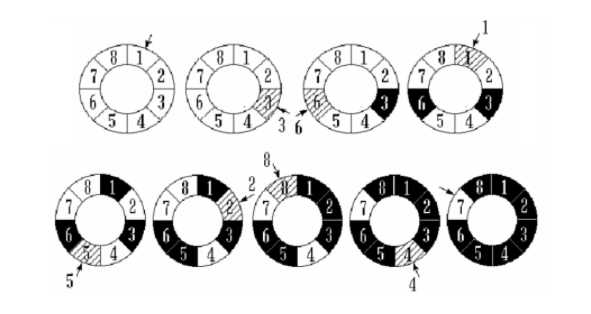
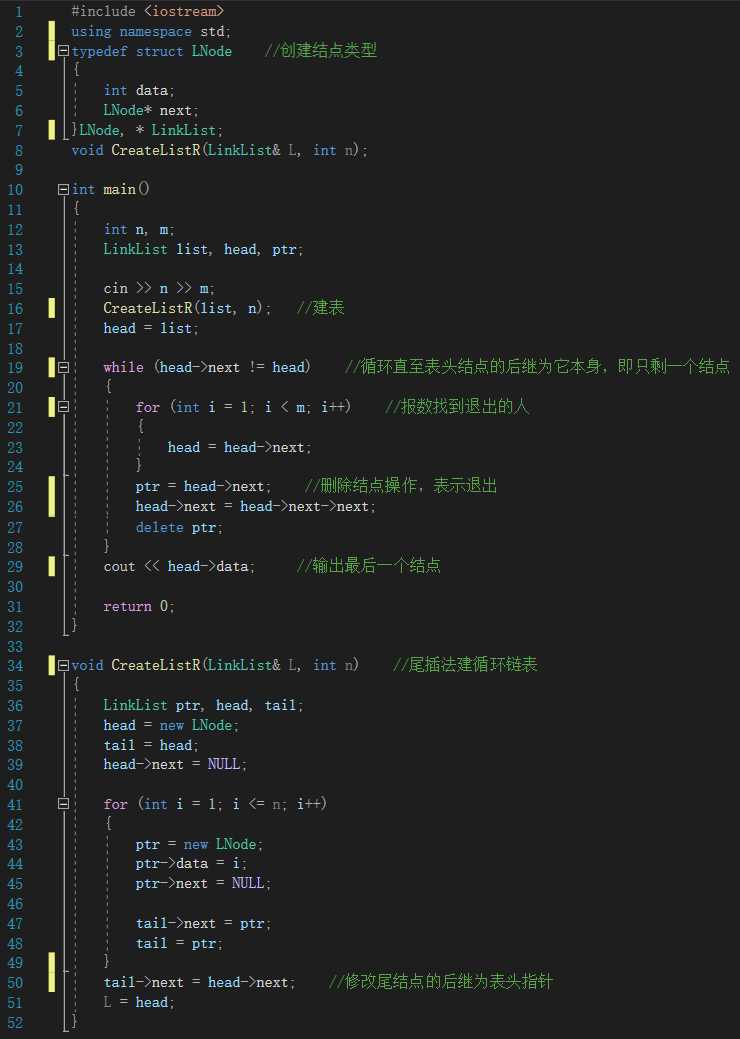
对于这个问题我们肯定是要用一个线性表的,从1开始存储到第 n 号数据,表示 n 个按顺序排列的人。由于涉及到人的退出,我们当然可以用数组来实现,通过修改元素的数值来标记是否退出,但是既然涉及到对数据的动态操作,我们可以采用更灵活的链表来实现,遇到需要退出的号数时,就直接把对应的结点删除即可。由于线性表遍历到最后一个元素时,需要复位到第一个元素,既然如此,我们就选择循环链表来实现即可,因为对于循环链表,尾结点的后继就是表头结点,这就使复位到表头结点的操作不需要额外的分支结构就能实现。
还记得我小学的时候写过这样一道数学题:
假设有一条公交线路由A车站到B车站,两个车站之间还有6个车站,请问需要设计多少种车票?
当时我很快就画出草图,写出算式“7+6+5+4+3+2+1=28”,用排列组合的知识来看,这么列式子是合理的,很可惜这是错误答案!我忽略了一个重要问题,搭乘公交车,既可以从起点站坐到终点站,也可以从终点站反向搭回起点站,公交线路是双向的,我的答案没有考虑返程的情况啊。
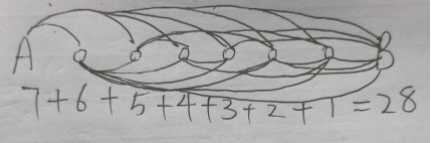
如果我们需要获取单链表中某个结点的上一个结点,我们就需要从头开始,再次遍历一遍,如果这个结点接近表尾,那么时间的花费就显得太大了,我们的链表可以“返程”吗?很自然,我们能够使用指针找到存储位置不相邻,但是逻辑上相邻的下一个结点,当然也可以利用指针找到上一个结点了。

双向链表的实现,是在单链表结点的基础上再添加一个指针域,该指针域用于指向前驱结点,这里体现了空间换时间的思想,虽然前驱指针域需要占用一定的空间,但是对于一些功能的实现提供了方便,而且效率更高。

结构体定义如下:
typedef struct DulNode
{
ElemType data;
struct DulNode *prior; //前驱指针域
struct DulNode *next; //后继指针域
}DulNode,*DulList;
由于多了一个指针域,因此初始化的时候两个指针域都要初始化,那我们就直接造个循环双向链表出来吧。
List MakeEmpty()
{
List head;
head = new LNode; //为头结点申请空间
head->next = head; //后继指针域初始化为头结点
head->prior = head; //前驱指针域初始化为头结点
return head;
}
根据我们一开始提出的思想:复杂的操作是由基本操作组合而成。双向链表虽然多了一个指针域,需要额外描述结点与前驱结点的逻辑关系,但是在操作上也并不复杂,无非是在修改与后继结点的逻辑关系上再多修改与前驱结点的逻辑关系而已。需要牢记的是,我们做插入删除操作时思路要清晰,顺序不能乱。
假设需要插入新结点 ptr,插入位置是 list 和 list->next 两个结点之间。
ptr->prior = list; //修改 ptr 的前驱为 list
ptr->next = list->next; //修改 ptr 的后继为 list->next
list->next->prior = ptr; //修改 list->next 的前驱为 ptr
list->next = ptr; //修改 list 的后继为 ptr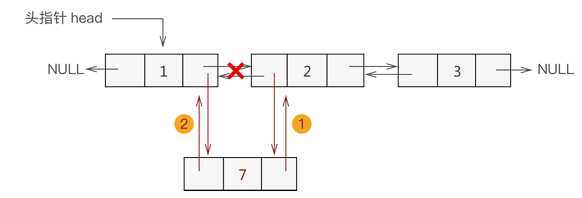
假设要删除双向链表的结点 ptr,只需要把 ptr 结点的前驱和后继安排明白即可。
ptr->prior->next = ptr->next; //修改 ptr 前驱的后继为 ptr->next
ptr->next->prior = ptr->prior; //修改 ptr 后继的前驱为 ptr->prior
delete ptr; //释放 ptr 的空间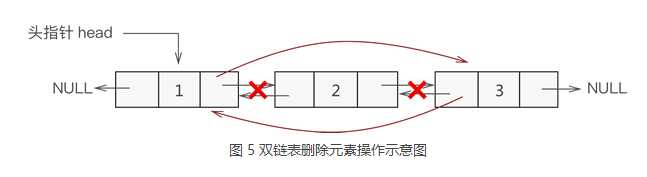
在 C/C++ 中,我们可以利用数组实现顺序表,用指针实现链表,但是并不是所有语言都有这两种工具的,例如 python、Java 等,不过这些是面向对象的世界语言,拥有其他机制来实现指针的功能,但是对一些早期的编程语言来说,上述的链表就没有办法实现了。如果我想要在不能使用指针的情况下使用链式存储结构,应该怎么操作呢?
可以用数组代替指针实现链式存储结构,我们说链式存储结构的特点在于,存储位置可以不相邻,数据间的逻辑关系可以被描述,只要我们利用数组实现这两个需求,就可以达到用数组实现链式存储结构的目的。
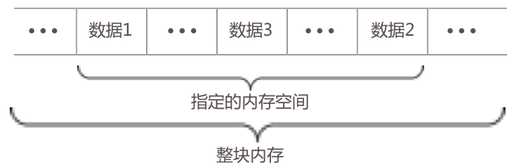
我们定义一个结构体,这个结构体拥有两个数据域 data 和 cur,data 用来存放需要存储的数据,而 cur 则用来存储该元素对应的后继在数组中的下标,也就是说 cur 数据域相当于单链表的指针域,通过 cur 我们就能找到该元素对应的后继。cur 被称为游标,用数组实现的链式存储结构被称为静态链表。
typedef struct
{
ElemType data; //数据域
int cur; //游标
}Component,StaticList[MAXSIZE]; //为了防止溢出,数组的存储上限可以定义的大一些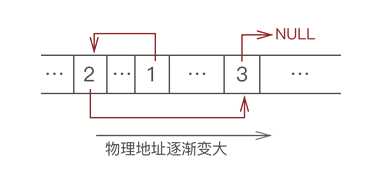
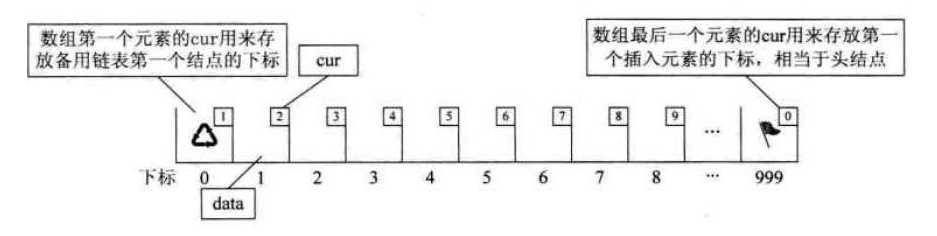
静态链表能否实现类似单链表的申请、释放结点的功能,可以将这个数组分为两部分,一部分用来存储数据,另一部分作为备用链表。备用链表,即连接各个空闲位置的链表,备用链表的作用是回收数组中未被使用的存储空间,作为提供新结点的空间来源。每当我们需要新结点的时候,就把备用链表中的一个元素通过游标接入到存储数据的表上来。这个时候,就要求我们能够精准定位两个表在同一个数组中的位置,可以利用数组的第一个元素作为头结点,用于定位备用链表,用 cur 记录备用链表的第一个结点的下标,最后一个元素则充当头结点,用于定位存储数据的表,cur 存储第一个存储数据的第一个结点下标。
bool InitLinst(StaticList L)
{
int i;
for(i = 0; i < MAXSIZE - 1; i++)
{
L[i].cur = i + 1; //初始化游标
}
L[MAXSIZE - 1].cur = 0; //最后一个元素充当头结点,cur 初始化为0
}当我们需要新结点的时候,就利用修改游标的关系,把备用链表的一个元素连接到主表上,删除则是把不再使用的元素用游标转移到备用链表。由此可见插入和删除操作都要特别注意对游标的精准操作操作。
首先我们需要先模拟实现动态内存分配函数 malloc,以此实现对备用链表申请空间,函数返回备用链表中第一个结点的下标,如果备用链表没有闲置空间了,就返回0。
int SSL_Malloc(StaticList space)
{
int idx = space[0].cur; //将备用链表的第一个闲置空间的下标作为返回值,表示申请到的空间
if(space[0].cur != 0) //判断备用链表的闲置空间是否用尽
{
space[0].cur = space[idx].cur; //若没用尽,移动备用链表的第一个结点为原第一个结点的后继
}
return idx; //返回可利用的数组元素下标
}我们自己造了动态内存分配函数,接下来就实现静态链表的插入结点,与单链表插入结点的思路一致,不同在于我们操作的不是指针域,而是游标。函数成功插入结点时返回 true,否则返回 false。
bool LinkInsert(StaticLinkList L,int idx, ElemType e)
{
int blank; //存储分配好的空闲空间下标
int prior = MAXSIZE - 1; //存储需要插入的前驱结点下标,初始化为最后一个元素
if(i < 1 || i > ListLength(L) + 1) //处理不合法插入
{
return false;
}
blank = SSL_Malloc(L); //分配空闲的元素下标
if(blank != 0)
{
L[blank].data = e; //向新节点放入数据
for(int i = 1; i <= idx - 1; i++) //获取前驱结点下标
{
prior = L[prior].cur; //通过游标遍历静态链表,直到找到 idx 的前驱
}
L[blank].cur = L[prior].cur; //修改新新结点的后继为前驱结点的后继
L[prior].cur = blank; //修改前驱结点的后继为新结点
return true;
}
return false;
}首先我们需要先实现结点释放函数 SSL_Free,实现的方式还是对游标的精确操作。
void SSL_Free(StaticLink L, int i)
{
space[i].cur = space[0].cur; //运用头插法的思想,修改被释放的结点的后继为备用链表的第一个结点
space[0].cur = i; //修改备用链表的第一个结点为被释放的结点
}删除静态链表中第 i 个元素,删除的位置不合法返回 false,成功删除返回 true。
bool LinkDelete(StaticLink L, int idx)
{
int prior;
if(idx < 1 || idx > ListLength(L))
{
return false;
}
prior = MAXSIZE - 1;
for(int i = 1; i <= idx - 1; i++)
{
prior = L[prior].cur; //遍历静态链表,找到第 idx 位置的前驱
}
i = L[prior].cur; //拷贝需要转移到备用链表的元素下标
L[prior].cur = L[L[prior].cur].cur; //修改前驱结点的游标为结点后继的后继
SSL_Free(L,i); //转移元素到备用链表
return true;
}静态链表通过一个 int 类型的变量作为游标,代替了链表中指针的使用,使得数组也可以实现链式存储结构,使得数组描述的线性表在执行插入、删除操作时,不需要移动大量元素,但是静态链表并不能解决存储数据数量的上限所带来的问题,而且也失去了数组在随机读取方面的优势。静态链表是为了在没有指针及其类似语法的时候,实现链式存储结构的方式,但是目前已经很少应用这种存储结构了,不过我们对于这种别致的线性表,我们没有用到什么复杂的语法,而是灵活的应用了数组及其下标,这就强调了复杂的操作是由基本操作组合而成这种思想。
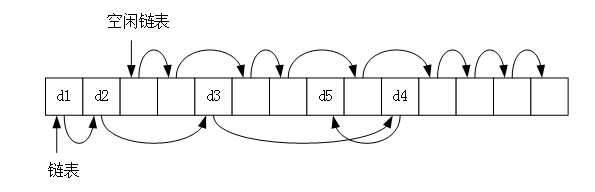
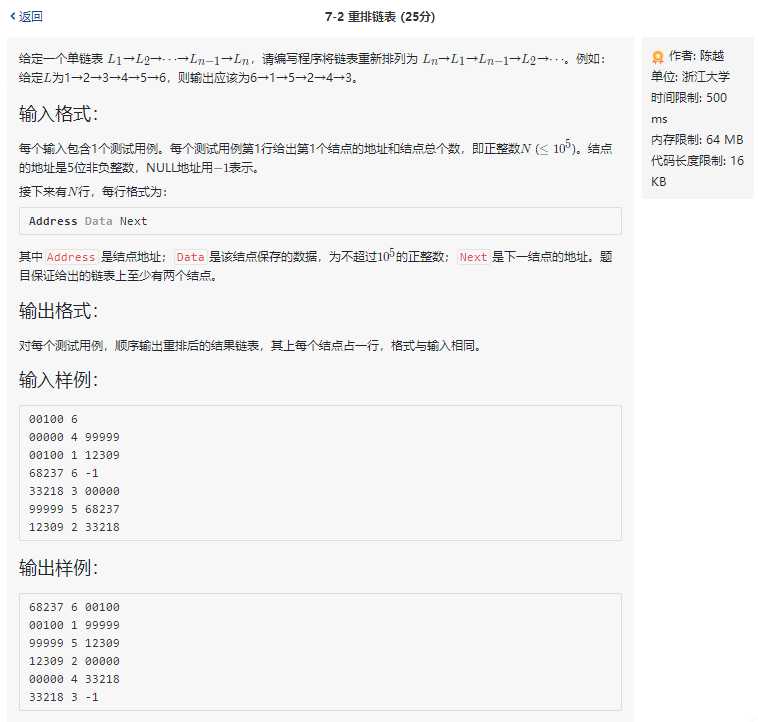
我们来看看这道题目吧,这道题目的测试数据很别致,测试数据已经把链表单个结点的地址及其后继安排得明明白白了,那么这种数据我们用什么结构存储是最合适的?那就是静态链表,我可以开一个元素个数为100000的空间,然后按照每一组数据的结点地址,相对应位置的数组元素填充,数组元素包含两个域,分别是数据域和游标,利用游标来存储下一个结点在数组中的位置。
这样我们就把数据安排明白了,我们发现这么存数据并不是严格意义上的静态链表,因为我们在这个数组中构造备用链表。这是因为给的测试数据已经把结点的逻辑关系描述得很明白了,而且不会引入新结点,所以我们也不必多此一举,去描述备用链表。我们是虽然没有实现完整的静态链表,但是我们利用了静态链表的思想去解决这个问题。
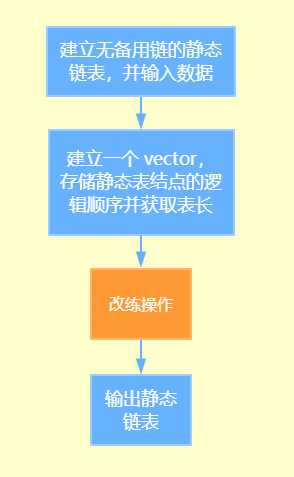
接下来就要重排链表了,不过如果直接去遍历这个链表,并修改结点,那就会出现很多问题,我们当然可以造个尾游标,从头和尾向中间移动,依次获取对应改链,但是这样无疑是很麻烦的。思考一下,如果我们已经实现知道了静态表的逻辑顺序,然后直接找到各个结点修改游标,修改的数值直接可以通过静态表的逻辑顺序来查找修改,这样就方便了很多。所以,我们可以造一个 vector 来按照表的逻辑顺序获取地址,用 vector 的目的在于,提供的数据可能有废弃结点,这种结点不会包含在表中,因此我们的思路是遍历到一个结点,就向 vector 中动态加入一个元素,由于 vector 容器是动态增长的容器,因此也不会造成空间的浪费。在获取了静态链表结点的逻辑顺序之后,我们也可以直接利用泛型算法“ .size() ”直接获取表长。
有了表长和结点的逻辑顺序,就可以通过对各个结点地址的访问,轻松达到改链的目的,我们可以对两端同时操作,一次安排两个结点,然后向中间移动。需要注意的是,如果是这么操作的话,尾结点就会丢失,也就是尾结点的后继不为 NULL,遍历时就会陷入死循环,这是我们不希望看到的。因此我们需要找到尾结点,将尾结点的后继修改为 -1。
最后,把静态表输出,大功告成!


调试到对才交的,调试遇到的问题
Q1:输出静态链表时,尾结点会进入死循环
A1:由于按照循环改链的方式,尾结点的后继不会被修改为 NULL,因此需要单独造个分支结构修改
Q2:结点的逻辑顺序保存操作麻烦
A2:原本使用数组保存,后来发现使用 vector 操作效率高且便捷,修改即可
阅读代码部分,左转我的另一篇博客SkipList (跳跃表)解析及其实现。


我们需要去理解和体会复杂的操作是有简单的操作组合而成这种思想,接着我们要去深刻体会链表的特点,链表是一个动态的结构,链表结点的插入删除操作极其方便,因此我们可以将结点从一个表中移动到另一个结点。

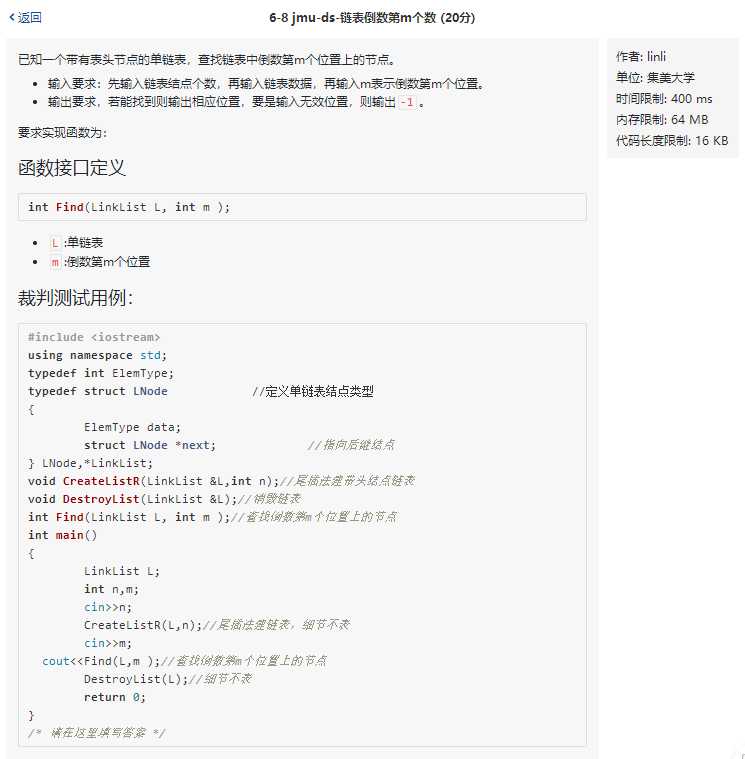
刚看到这道题,我们最直观的想法是,先遍历一遍链表,统计表长,然后再一次遍历链表,遍历到倒数第 n 个结点之后返回对应的数值,所以我们可以很自然地写出这样的代码。
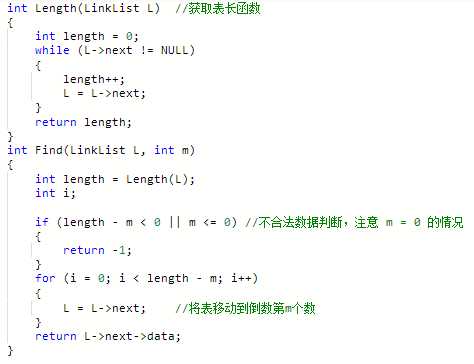
但是,如果是这么搞的话,就不可避免地遍历2遍链表,第一次遍历只是为了获取表长,然后第二次访问对应结点,这两个操作很相似,但是由于我们不知道表长,本质上也就是不知道尾结点在哪里,我们只能先定位尾结点,再访问。那么,我们现在的想法是,如何在定位到尾结点的同时,就能够找到倒数第 n 个结点呢?

我们来想一个问题,如果在一个跑道上有两位运动员,这两位运动员的跑步速度始终是一样的。在起跑的时候,一位运动员先跑 10m,另一位再开始跑,由于两位运动员速度始终相同,因此他们的路程差始终是 10m。我们定义两个指针,把一个线性表抽象成跑道,两个指针抽象成运动员,我们让其中一个指针先遍历 n 个结点,之后另一个指针苏醒,两个指针同时遍历线性表,它们的步长相等。当先开始遍历的指针遍历到尾结点的时候,后开始遍历的指针所在的位置就是第 (表长-步差) 个结点,这个结点就是倒数第 n 个结点了。
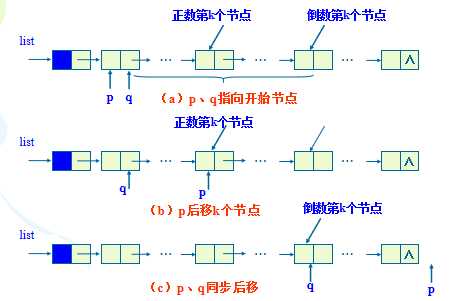
在遍历同一个线性表的时候,对于两个指针的步长和步差有差异,我们把这样的两个特殊的指针成为快指针和慢指针。本题的快、慢指针的步长相同,步差为一个定值,除了本题的用法,例如快、慢指针的步差为 0,但是快指针的步长为慢指针的2倍,当快指针遍历完线性表时,慢指针所在的位置就是中位结点。灵活应用快、慢指针,我们可以巧妙地忽略一些不必要的操作,提高我们的效率。

Q1:对于不合法数据判定不正确
A1:不合法数据除了 m 为负数的情况之外,还有 m 的大小超过了表长,第二种情况我没有考虑,补上一个分支结构即可。
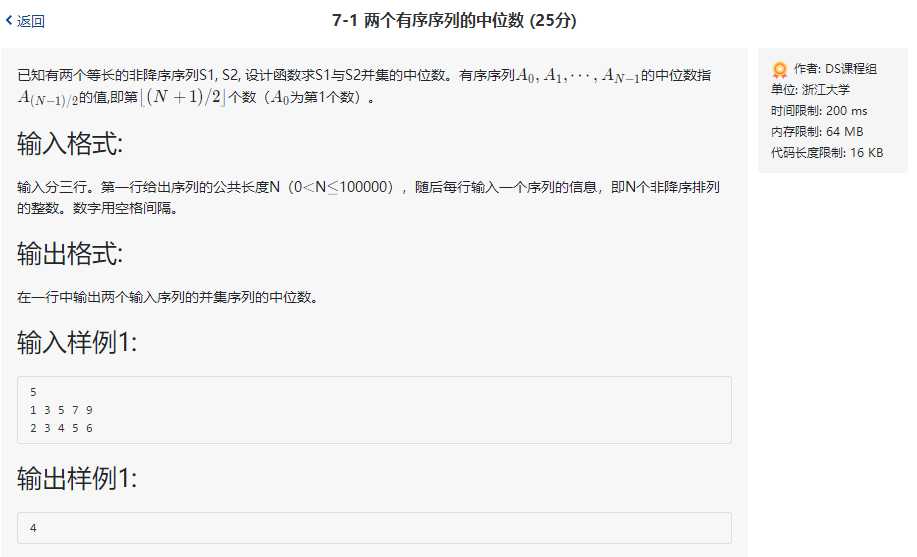
看到题干,我们最直观的想法是,直接把两个线性表存起来,然后给这两个表排序,排序结束后我们就能直接获取有序表的中位数了。但是如果数据规模很大,排序算法的效率太低,就会有超时的风险,好在 STL 库给我们提供了泛型算法,让我们可以直接享受快速排序的便捷。代码如下:
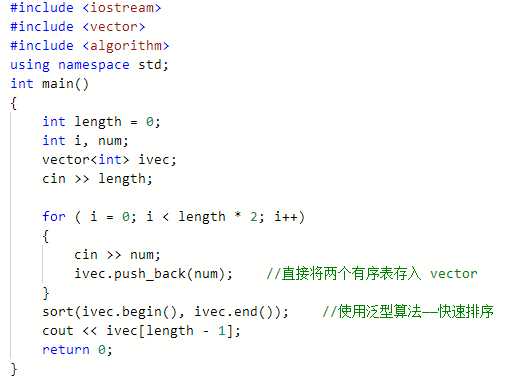
不过,这种做法虽然可以实现目的,但是这是个可惜的做法,因为输入的数据是有序的,可是我们非要绕远路,把有序的逻辑打乱,再重新整合,其实只需要一个二路归并算法即可实现。那么我们来想一个问题,我们的目的是找到中位数,我们需要将两个有序表完整地归并吗?大可不必。

仔细观察,我们只归并两个有序表的前半部分,那么这两个表的中位数必定被包含在其中,而且是在表尾的位置,所以我们的工作量折半了,虽然时间复杂度不变,但是效率确实又提升了一步。


Q1:编译错误
A1:选错了编译器
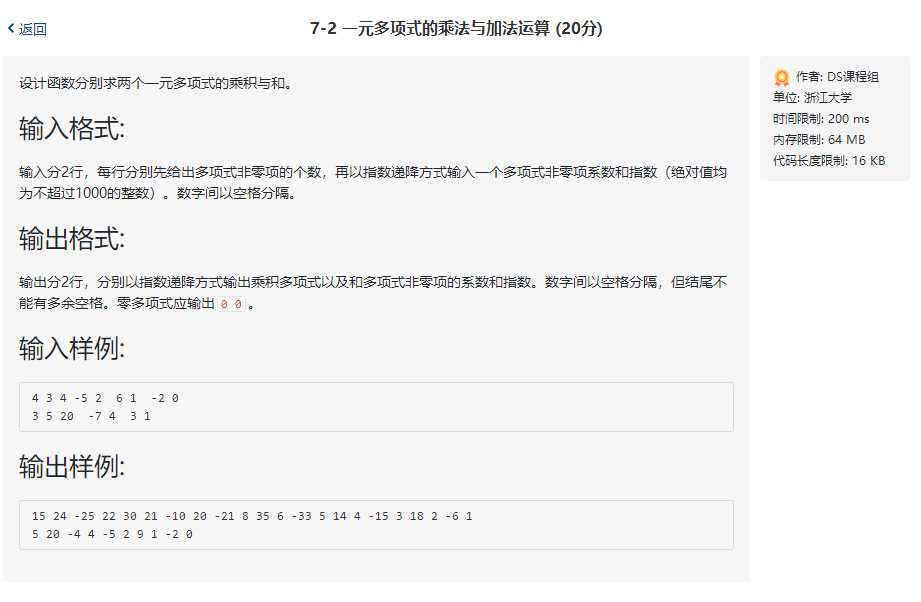
| 测试数据 | 说明 |
|---|---|
| 4 3 4 -5 2 6 1 -2 0 3 5 20 -7 4 3 1 |
sample |
| 2 2 2 -2 1 2 2 2 2 1 |
同类项合并时有抵消 |
| 0 1 1 1 |
输入输出有零多项式 |
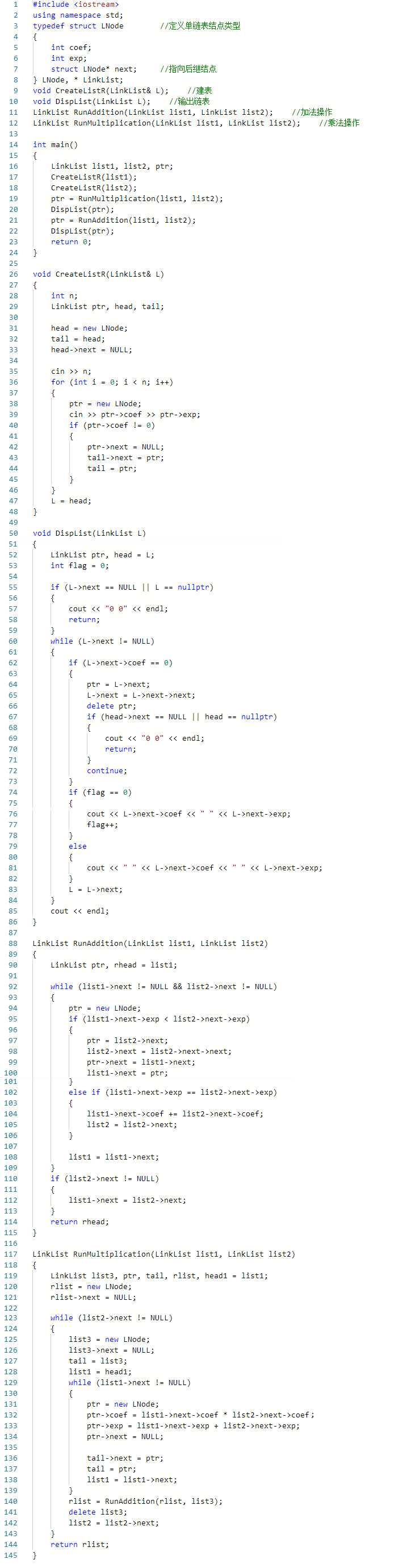
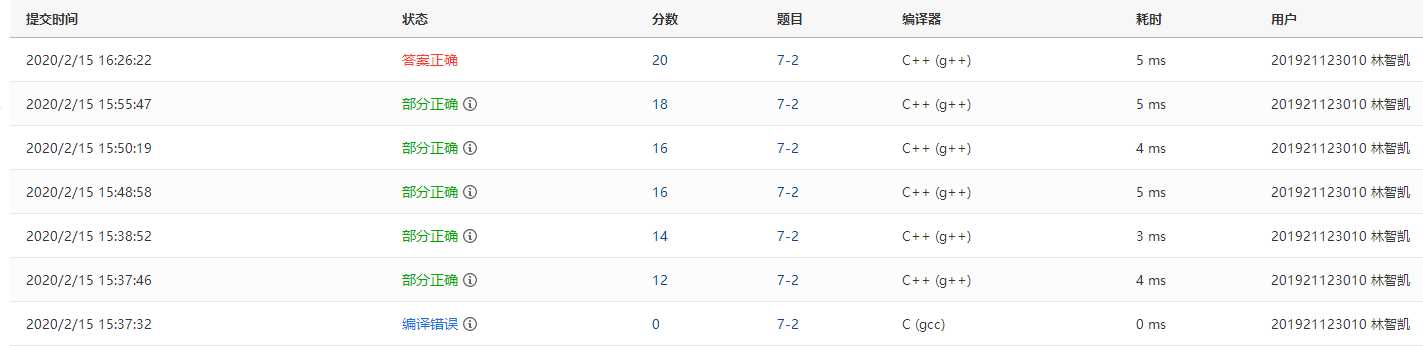
Q1:写乘法操作时,无法正确地同时完成乘法运算和合并同列项
A1:建一个新表,将表2的所有结点依次与表1的所有结点完成乘法操作,将结果接到一个新表上,然后调用加法函数,合并新表和保存运算结果的表
Q2:对于合并同列项需要抵消的结点无法准确删除
A2:原计划是出现需要抵消的结点,就马上释放,但是我最终没有实现,最后改变策略,即使出现了需要抵消的结点也暂时不处理,然后在输出的时候判断系数是否为 0,若为 0 则删除结点。结合我的两个特殊的测试数据,将程序调试到正确。
《大话数据结构》—— 程杰 著,清华大学出版社
《数据结构教程》—— 李春葆 主编,清华大学出版社
《数据结构与算法》—— 王曙燕 主编,人民邮电出版社
线性表之顺序表与单链表的区别及优缺点
数据结构6: 静态链表及C语言实现
C语言中文网
标签:定义 最简 百度 必须 主表 strong 注意 回收 while
原文地址:https://www.cnblogs.com/linfangnan/p/12316614.html