标签:lin tle 时间 例子 线图 expand 综合 方法 adjust
对比分析 → 两个互相联系的指标进行比较
绝对数比较(相减) / 相对数比较(相除) 结构分析、比例分析、空间比较分析、动态对比分析
相互对比的指标在量级上不能差别过大
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
data = pd.DataFrame(np.random.rand(30,2)*1000,
columns = [‘A_sale‘,‘B_sale‘],
index = pd.period_range(‘20170601‘,‘20170630‘))
print(data.head())
?
# 创建数据 → 30天内A/B产品的日销售额
?
data.plot(kind=‘line‘,
style = ‘--.‘,
alpha = 0.8,
figsize = (10,3),
title = ‘AB产品销量对比-折线图‘)
?
# 折线图比较
?
data.plot(kind = ‘bar‘,
width = 0.8,
alpha = 0.8,
figsize = (10,3),
title = ‘AB产品销量对比-柱状图‘)
?
# 多系列柱状图比较
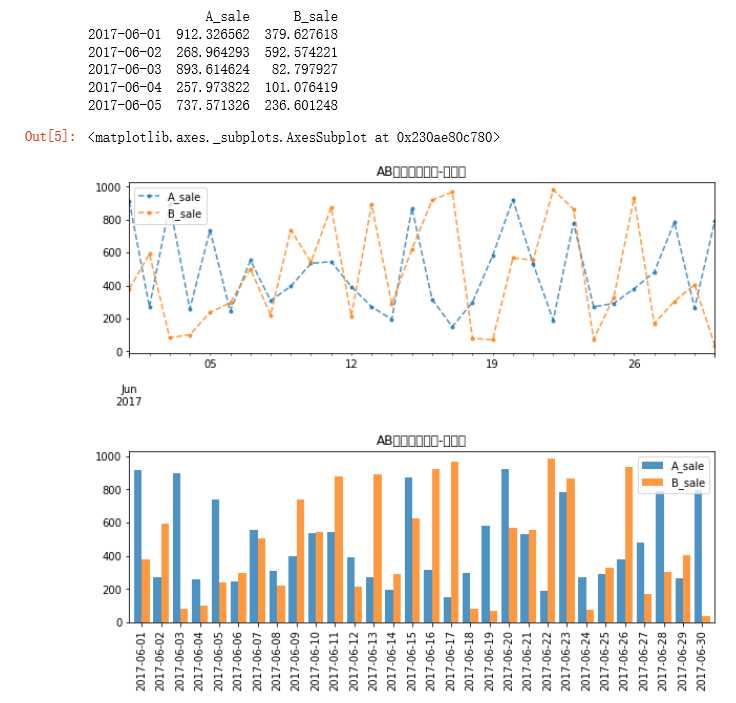
fig3 = plt.figure(figsize=(10,6))
plt.subplots_adjust(hspace=0.3)
?
# 创建子图及间隔设置
?
ax1 = fig3.add_subplot(2,1,1)
x = range(len(data))
y1 = data[‘A_sale‘]
y2 = -data[‘B_sale‘]
plt.bar(x,y1,width = 1,facecolor = ‘yellowgreen‘)
plt.bar(x,y2,width = 1,facecolor = ‘lightskyblue‘)
plt.title(‘AB产品销量对比-堆叠图‘)
plt.grid()
plt.xticks(range(0,30,6))
ax1.set_xticklabels(data.index[::6])
?
# 创建堆叠图
?
ax2 = fig3.add_subplot(2,1,2)
y3 = data[‘A_sale‘]-data[‘B_sale‘]
plt.plot(x,y3,‘--go‘)
plt.axhline(0,hold=None,color=‘r‘,linestyle="--",alpha=0.8) # 添加y轴参考线
plt.grid()
plt.title(‘AB产品销量对比-差值折线‘)
plt.xticks(range(0,30,6))
ax2.set_xticklabels(data.index[::6])
?
# 创建差值折线图
有联系的指标综合计算后的对比,数值为相对数
结构分析、比例分析、空间比较分析、动态对比分析、计划完成度分析
在分组基础上,各组总量指标与总体的总量指标对比,计算出各组数量在总量中所占比重
反映总体的内部结构
data = pd.DataFrame({‘A_sale‘:np.random.rand(30)*1000,
‘B_sale‘:np.random.rand(30)*200},
index = pd.period_range(‘20170601‘,‘20170630‘))
print(data.head())
print(‘------‘)
?
# 创建数据 → 30天内A/B产品的日销售额
?
# A/B产品销售额量级不同
?
data[‘A_per‘] = data[‘A_sale‘] / data[‘A_sale‘].sum()
data[‘B_per‘] = data[‘B_sale‘] / data[‘B_sale‘].sum()
?
# 计算出每天的营收占比
?
data[‘A_per%‘] = data[‘A_per‘].apply(lambda x: ‘%.2f%%‘ % (x*100))
data[‘B_per%‘] = data[‘B_per‘].apply(lambda x: ‘%.2f%%‘ % (x*100))
?
# 转换为百分数
?
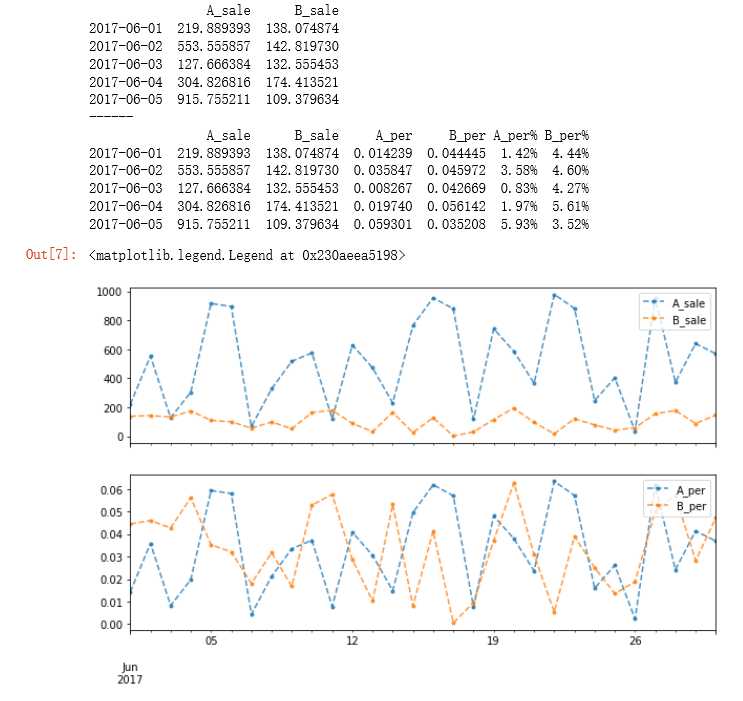
print(data.head())
?
fig,axes = plt.subplots(2,1,figsize = (10,6),sharex=True)
data[[‘A_sale‘,‘B_sale‘]].plot(kind=‘line‘,style = ‘--.‘,alpha = 0.8,ax=axes[0])
axes[0].legend(loc = ‘upper right‘)
data[[‘A_per‘,‘B_per‘]].plot(kind=‘line‘,style = ‘--.‘,alpha = 0.8,ax=axes[1])
axes[1].legend(loc = ‘upper right‘)
?
# 绝对值对比较难看出结构性变化,通过看销售额占比来看售卖情况的对比
?
# 同时可以反应“强度” → 两个性质不同但有一定联系的总量指标对比,用来说明“强度”、“密度”、“普遍程度”
?
# 例如:国内生产总值“元/人”,人口密度“人/平方公里
在分组的基础上,将总体不同部分的指标数值进行对比,其相对指标一般称为“比例相对数”
比例相对数 = 总体中某一部分数值 / 总体中另一部分数值 → “基本建设投资额中工业、农业、教育投资的比例”、“男女比例”...
data = pd.DataFrame({‘consumption‘:np.random.rand(12)*1000 + 2000,
‘salary‘:np.random.rand(12)*500 + 5000},
index = pd.period_range(‘2017/1‘,‘2017/12‘,freq = ‘M‘))
print(data.head())
print(‘------‘)
?
# 创建数据 → 某人一年内的消费、工资薪水情况
?
# 消费按照2000-3000/月随机,工资按照5000-5500/月随机
?
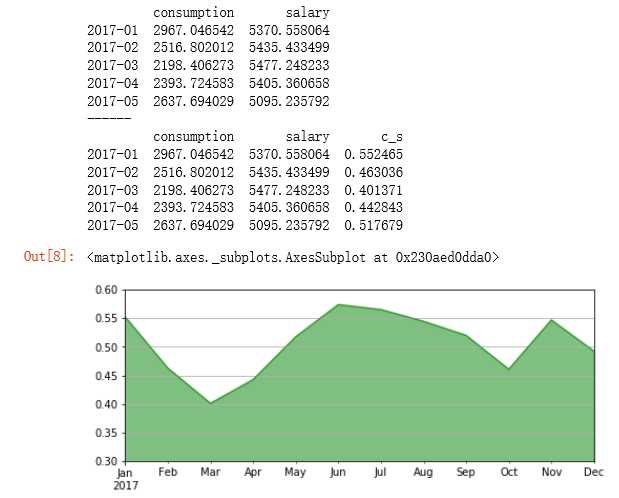
data[‘c_s‘] = data[‘consumption‘] / data[‘salary‘]
print(data.head())
?
# 比例相对数 → 消费收入比
?
data[‘c_s‘].plot.area(color = ‘green‘,alpha = 0.5,ylim = [0.3,0.6],figsize=(8,3),grid=True)
?
# 创建面积图表达
同类现象在同一时间不同空间的指标数值进行对比,反应同类现象在不同空间上的差异程度和现象发展不平衡的状况
空间比较相对数 = 甲空间某一现象的数值 / 乙空间同类现象的数值
一个很现实的例子 → 绝对数来看,我国多经济总量世界第一,但从人均水平来看是另一回事
同比 → 产品A在2015.3和2016.3的比较(相邻时间段的同一时间点)
环比 → 产品A在2015.3和2015.4的比较(相邻时间段的比较)
如何界定“相邻时间段”与“时间点”,决定了是同比还是环比
data = pd.DataFrame({‘A‘:np.random.rand(30)*5000,
‘B‘:np.random.rand(30)*2000,
‘C‘:np.random.rand(30)*10000,
‘D‘:np.random.rand(30)*800},
index = pd.period_range(‘20170601‘,‘20170630‘))
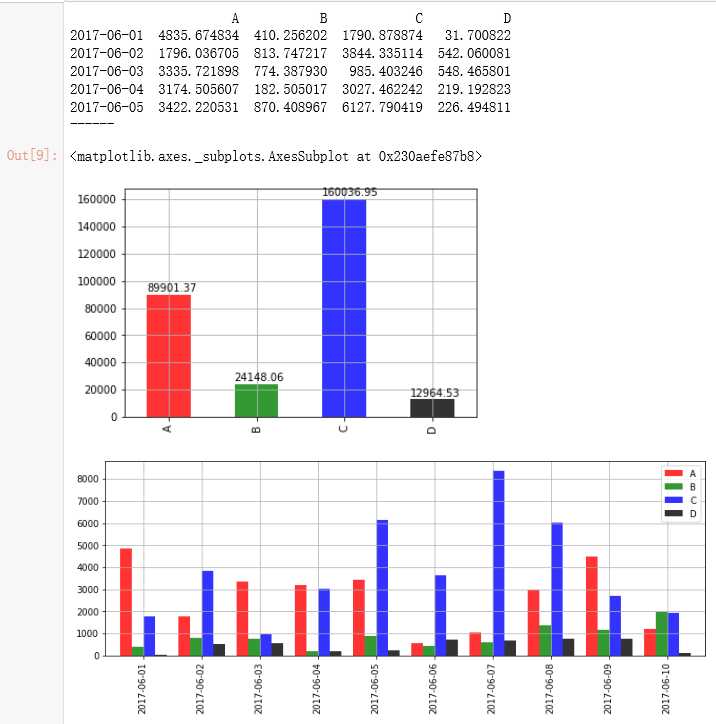
print(data.head())
print(‘------‘)
?
# 创建数据 → 30天内A/B/C/D四个产品的销售情况
?
# 不同产品的销售量级不同
?
data.sum().plot(kind = ‘bar‘,color = [‘r‘,‘g‘,‘b‘,‘k‘], alpha = 0.8, grid = True)
for i,j in zip(range(4),data.sum()):
plt.text(i-0.25,j+2000,‘%.2f‘ % j, color = ‘k‘)
?
# 通过柱状图做横向比较 → 4个产品的销售额总量
?
data[:10].plot(kind = ‘bar‘,color = [‘r‘,‘g‘,‘b‘,‘k‘], alpha = 0.8, grid = True, figsize = (12,4),width = 0.8)
?
# 多系列柱状图,横向比较前十天4个产品的销售额
?
同一现象在不同时间上的指标数值进行对比,反应现象的数量随着时间推移而发展变动的程度及趋势
最基本方法,计算动态相对数 → 发展速度
动态相对数(发展速度) = 某一现象的报告期数值 / 同一现象的基期数值
基期:用来比较的基础时期
报告期:所要研究的时期,又称计算期
data = pd.DataFrame({‘A‘:np.random.rand(30)*2000+1000},
index = pd.period_range(‘20170601‘,‘20170630‘))
print(data.head())
print(‘------‘)
?
# 创建数据 → 30天内A产品的销售情况
?
data[‘base‘] = 1000 # 假设基期销售额为1000,后面每一天都为计算期
data[‘l_growth‘] = data[‘A‘] - data[‘base‘] # 累计增长量 = 报告期水平 - 固定基期水平
data[‘z_growth‘] = data[‘A‘] - data.shift(1)[‘A‘] # 逐期增长量 = 报告期水平 - 报告期前一期水平
data[data.isnull()] = 0 # 替换缺失值
?
data[[‘l_growth‘,‘z_growth‘]].plot(figsize = (10,4),style = ‘--.‘,alpha = 0.8)
plt.axhline(0,hold=None,color=‘r‘,linestyle="--",alpha=0.8) # 添加y轴参考线
plt.legend(loc = ‘lower left‘)
plt.grid()
?
# 通过折线图查看增长量情况
?
data[‘lspeed‘] = data[‘l_growth‘] / data[‘base‘] # 定基增长速度
data[‘zspeed‘] = data[‘z_growth‘] / data.shift(1)[‘A‘] # 环比增长速度
data[[‘lspeed‘,‘zspeed‘]].plot(figsize = (10,4),style = ‘--.‘,alpha = 0.8)
plt.axhline(0,hold=None,color=‘r‘,linestyle="--",alpha=0.8) # 添加y轴参考线
plt.grid()
print(data.head())
print(‘------‘)
?
# 通过折线图查看发展速度
标签:lin tle 时间 例子 线图 expand 综合 方法 adjust
原文地址:https://www.cnblogs.com/Lilwhat/p/12442040.html