POJ2318 TOYS （计算几何）

题目大意：
给定一个矩形，这个矩形被 \(n\) 条线段（端点分别在矩形上下边界上）切割成 \(n+1\) 个块。再给你 \(m\) 个物品的坐标，问每个块中会有多少个物品，保证物品放置位置合法。

分析：

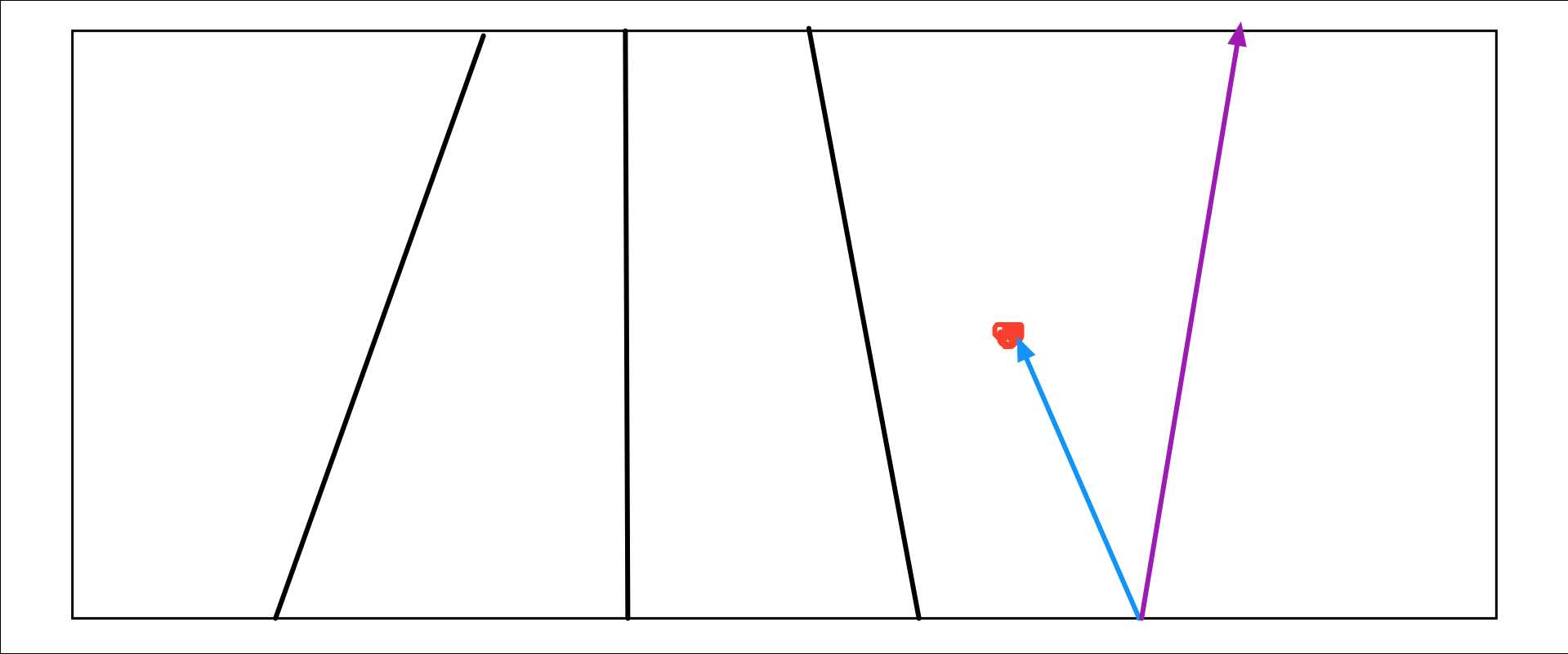
一个物品在一个块中时，他一定夹在两个分界线中间，且在左分界线的右边，右分界线的左边。故按图中那样，将物品连接某个边界下端，构成一个向量，再判断 蓝色向量 与 紫色向量 的位置关系，进行叉积即可。故二分找到第一个 物品向量 \(×\) 边界向量 为负的位置，即为该物品所在块的右边界（或者二分最后一个叉积为正的）。

代码如下：

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
#define pb push_back
#define first fi
#define second se
#define IO std::ios::sync_with_stdio(false)
typedef long long ll;
const int maxn = 100008;
const ll mod = 1e9+7;
const int inf = 0x3f3f3f3f;
const ll INF = 1e18 + 10;
const double eps = 1e-6;
using namespace std;
int n,m;
ll x1,y1,x2,y2;
struct Node{
    ll x,xx;
}nd[maxn];
struct Goods{
    ll x,y;
}a[maxn];
int sum[maxn];
bool judge(int i,int j){
    Goods e1,e2;
    e1.x=nd[j].x-nd[j].xx,e1.y=y1-y2;
    e2.x=a[i].x-nd[j].xx,e2.y=a[i].y-y2;
    ll ans=e2.x*e1.y-e2.y*e1.x;
    return ans>0;
}
int main()
{
    while(~scanf("%d",&n)&&n){
        scanf("%d%lld%lld%lld%lld",&m,&x1,&y1,&x2,&y2);
        memset(sum,0,sizeof(sum));
        nd[0].x=nd[0].xx=x1;
        nd[n+1].x=nd[n+1].xx=x2;
        for(int i=1;i<=n;i++) scanf("%lld%lld",&nd[i].x,&nd[i].xx);
        for(int i=1;i<=m;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
        for(int i=1;i<=m;i++){
            int l=0,r=n+1,mid;
            while(l<=r){
                mid=(l+r)/2;
                if(judge(i,mid)) l=mid+1;
                else r=mid-1;
            }
            sum[r]++;
        }
        for(int i=0;i<=n;i++) printf("%d: %d\n",i,sum[i] );
        putchar('\n');
    }
}

POJ2318 TOYS （计算几何）

标签：std   ret   using   关系   分界线   alt   false   problem   har   

原文地址：https://www.cnblogs.com/Absofuckinglutely/p/12442772.html