Red And Green解法

标签：tmp   inpu   复用   时间复杂度   ++   NPU   多少   图片   喷涂   

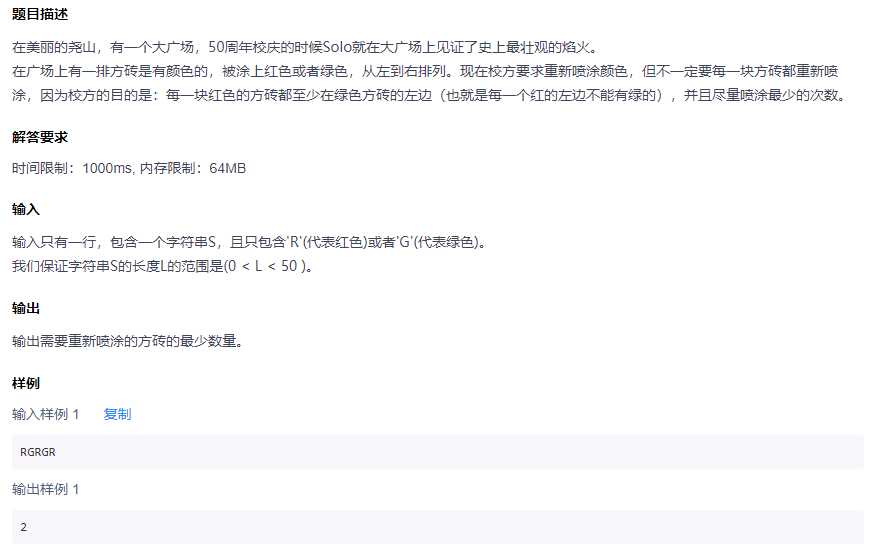
 #include <iostream>
#include <string>
using namespace std;

const long MAX_LEN = 50;

int main ()
{
    int Left[MAX_LEN] = {0};
    int Right[MAX_LEN] = {0};
    string input("");
    while (cin >> input) {
        int len = input.size();
        Left[0] = 0;
        Right[len] = 0;
        for (int i = 1; i <= len; ++i) {
            Left[i] = Left[i - 1] + (input[i - 1] == ‘R‘ ? 0 : 1);
            Right[len - i] = Right[len - i + 1] + (input[len - i] == ‘G‘ ? 0 : 1);
        }
        int ret = Left[0] + Right[0];

        for (int i = 0; i <= len; ++i) {
            int tmpRet = Left[i] + Right[i];
            if (tmpRet < ret) {
                ret = tmpRet;
            }
            //cout << "Left[" << i << "]:" << Left[i] << endl;
            //cout << "Right[" << i << "]:" << Right[i] << endl;
        }
        cout << ret << endl;
    }
    return 0;
}

// 假设有5个字符，那么肯定存在一个分界点，左边全是R，右边全是G，一共有6个节点可选
// 可以遍历出6个节点分别需要喷涂多少次，然后对比所有情况得到最小次数
// 常规解法：
//            节点遍历一次，每个节点遍历一次，时间复杂度是O(n^2)
//            这种解法每个节点会重复遍历，实际上后面的节点可以复用前面节点的次数，每次只需判断一个节点
// DP解法：
//             记r(i)是以第i个节点为分界点时，左边需要喷涂R的次数
//            记g(i)是以第i个节点为分界点时，右边需要喷涂G的次数
//             r(0)=0;    r(1)=r(0)+第0个字符的判断;    r(2)=r(1)+第1个字符的判断; r(i)=r(i-1)+第i-1个字符的判断;
//            g(5)=0; g(4)=g(5)+第4个字符的判断;  g(3)=g(4)+第3个字符的判断; g(i)=g(i+1)+第i个字符的判断;

Red And Green解法

标签：tmp   inpu   复用   时间复杂度   ++   NPU   多少   图片   喷涂   

原文地址：https://www.cnblogs.com/XPHouse/p/12446029.html