标签:ram org NPU you src length bug this cee
You are given two integers nn and dd . You need to construct a rooted binary tree consisting of nn vertices with a root at the vertex 11 and the sum of depths of all vertices equals to dd .
A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a vertex vv is the last different from vv vertex on the path from the root to the vertex vv . The depth of the vertex vv is the length of the path from the root to the vertex vv . Children of vertex vv are all vertices for which vv is the parent. The binary tree is such a tree that no vertex has more than 22 children.
You have to answer tt independent test cases.
The first line of the input contains one integer tt (1≤t≤10001≤t≤1000 ) — the number of test cases.
The only line of each test case contains two integers nn and dd (2≤n,d≤50002≤n,d≤5000 ) — the number of vertices in the tree and the required sum of depths of all vertices.
It is guaranteed that the sum of nn and the sum of dd both does not exceed 50005000 (∑n≤5000,∑d≤5000∑n≤5000,∑d≤5000 ).
For each test case, print the answer.
If it is impossible to construct such a tree, print "NO" (without quotes) in the first line. Otherwise, print "{YES}" in the first line. Then print n−1n−1 integers p2,p3,…,pnp2,p3,…,pn in the second line, where pipi is the parent of the vertex ii . Note that the sequence of parents you print should describe some binary tree.
3 5 7 10 19 10 18
YES 1 2 1 3 YES 1 2 3 3 9 9 2 1 6 NO
Pictures corresponding to the first and the second test cases of the example:
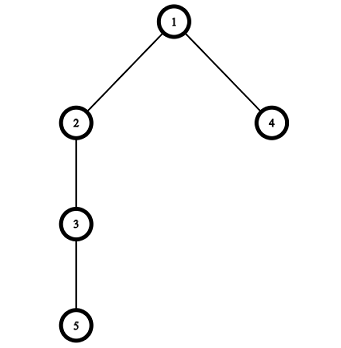
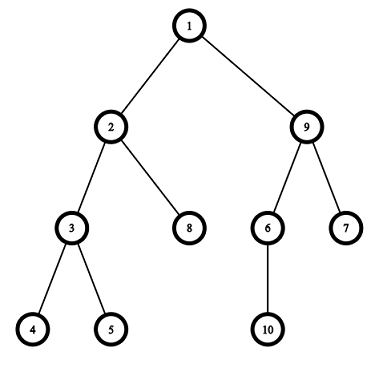
题解:
Tutorial
This problem has an easy constructive solution. We can find lower and upper bounds on the value of dd for the given nn. If the given dd does not belong to this segment, then the answer is "NO". Otherwise, the answer is "YES" for any dd in this segment.
How to construct it? Let‘s start from the chain. The answer for the chain is the upper bound of dd and it is n(n−1)2n(n−1)2. Then let‘s try to decrease the answer by 11 in one move. Let‘s take some leaf vv (the vertex without children) with the smallest depth that is not bad and try to move it up. The definition of badness will be below. To do this, let‘s find such vertex pp that its depth is less than the depth of vv by 22 and it has less than 22 children. If we found such vertex pp then let‘s make vv the child of pp and decrease the answer by one.
If we didn‘t find such vertex pp, I claim that the vertex vv has the minimum possible depth it can have and we should not consider it in the future. Let‘s mark this vertex as bad and continue our algorithm.
If at some moment we cannot find any not bad leaf vv, then the answer is "NO". Otherwise, the answer is "YES".
Time complexity: O(nd)O(nd).
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int t;
cin >> t;
while (t--) {
int n, d;
cin >> n >> d;
int ld = 0, rd = n * (n - 1) / 2;
for (int i = 1, cd = 0; i <= n; ++i) {
if (!(i & (i - 1))) ++cd;
ld += cd - 1;
}
if (!(ld <= d && d <= rd)) {
cout << "NO" << endl;
continue;
}
vector<int> par(n);
iota(par.begin(), par.end(), -1);
vector<int> cnt(n, 1);
cnt[n - 1] = 0;
vector<int> bad(n);
vector<int> dep(n);
iota(dep.begin(), dep.end(), 0);
int cur = n * (n