标签：sam ane 简单 i++ space span 输出 要求 for
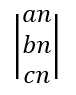
。那么
=
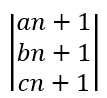
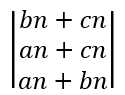
。也就是说n+1个格子的涂法f（n+1）=an+1+bn+1+cn+1=2（an+bn+cn）=2*f(n)
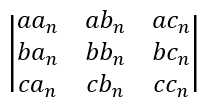
abn表示以红色为开头，粉色为结尾，长度为n的种类数。其他以此类推。f（n）=abn+acn+ban+bcn+can+cbn（n>1,首尾不能相同）。
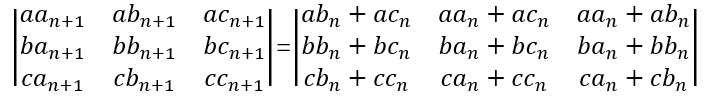
，从这个矩阵已经可以看出矩阵的三行是不相关的，是独立的，那么发现abn+1+acn+1=aan+acn+aan+abn=（abn+acn）+2*aan=（abn+acn）+2*(abn-1+acn-1).同理可得矩阵的第二行和第三行。解得：f（n+1）=f（n）+2f（n-1）。
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <vector> #include <cmath> #include <queue> #include <deque> #include <cmath> #include <map> using namespace std; typedef long long ll; const double inf=1e20; const int maxn=2e5+10; const int mod=1e9+7; ll a[100]; int main(){ a[0]=3; a[1]=a[2]=6; for(int i=3;i<60;i++){ a[i]=a[i-1]+2*a[i-2]; } int n; while(scanf("%d",&n)!=EOF){ printf("%lld\n",a[n-1]); } return 0; }
hdu 2045 不容易系列之(3)—— LELE的RPG难题
标签：sam ane 简单 i++ space span 输出 要求 for
原文地址：https://www.cnblogs.com/wz-archer/p/12447996.html
