标签:count 有一个 最大的 mat The 就会 理解 isp ubuntu
计算满足如下要求的序列的数量。
数据范围:\(2\leq n\leq m\leq 2e5\)。
对结果取\(mod\ 998244353\)。
首先特判,就是当\(n=2\)时,没有满足条件的序列,输出0。
来看一般情况,为了方便理解,我们画一张图。
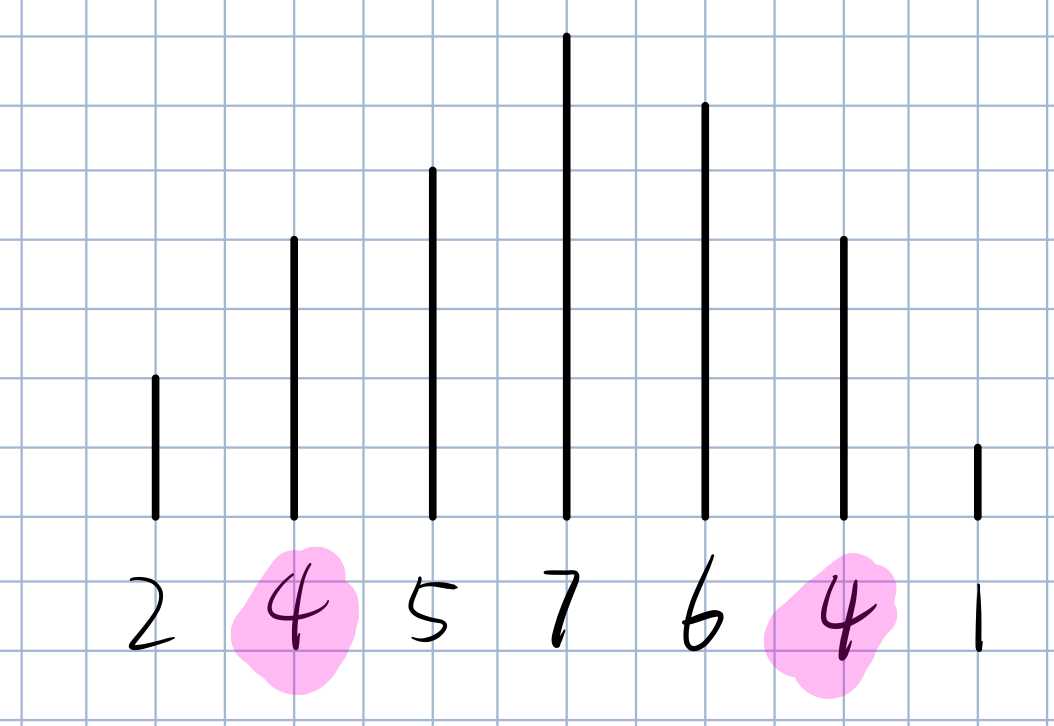
这是一个满足条件的序列,满足图像成山峰型,且仅一对数字相等。
我们可以发现,除了4相等之外,其他数字都是不同的。
所以我们可以转化一下。
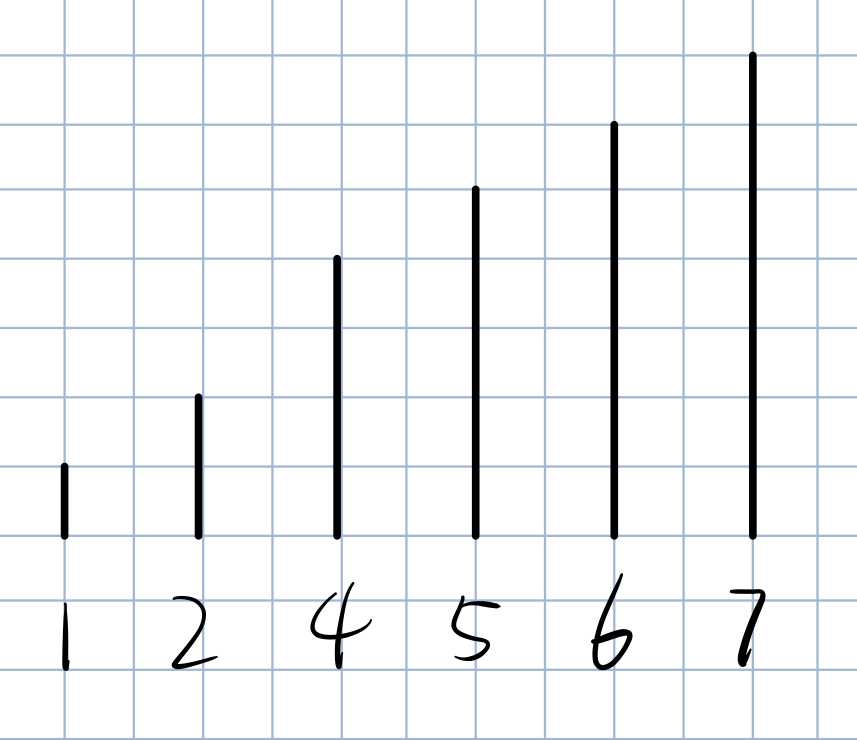
将其视为一个数字两两不同的递增序列,那满足这样条件的序列有多少种?
我们可以直接从\(m\)个数字中选\(n-1\)个出来,一定可以组成这样一个递增序列,所以答案是:
\[
C_{m}^{n-1}
\]
但是还有许多情况漏解,比如说我原序列有两个\(1\),得到的递增序列也是如上图所示。
那么我们就会发现,除了最大的数字之外,所有的数字都可以裂化为两个放到最大数字的右边,所以此时我们要对答案乘上\(n-2\)。如图所示:
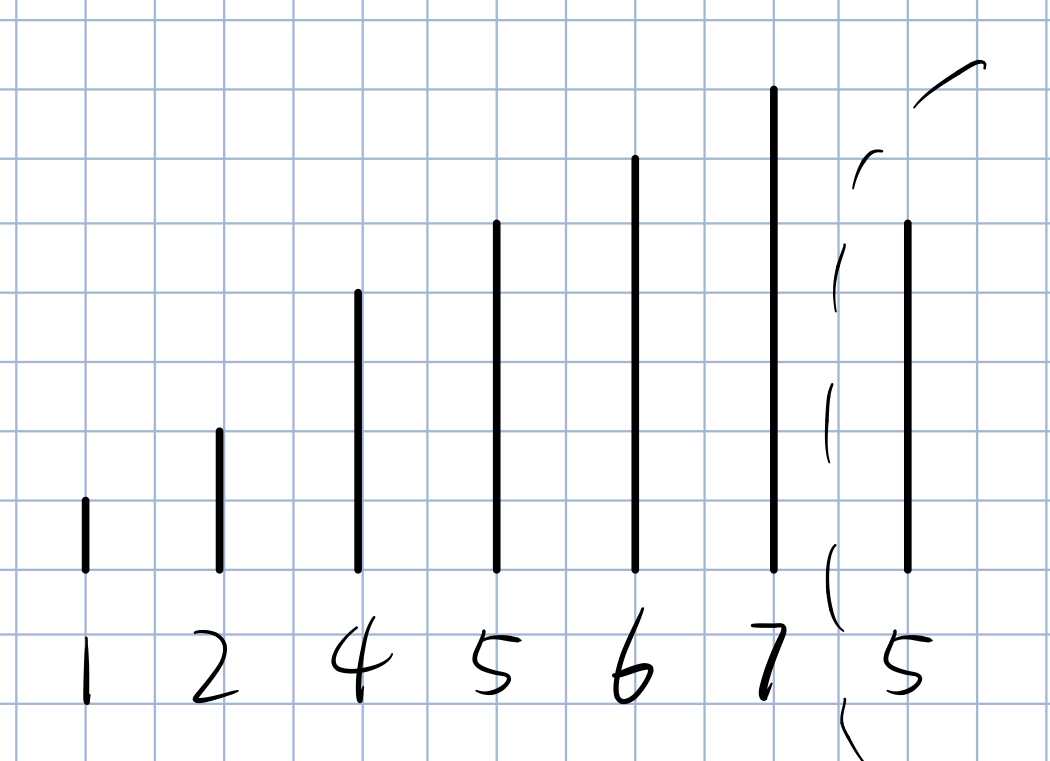
上图表示我们把一个5送到右边去。\(1,2,4,5,6\)都可以送到右边去。
此时还是会漏解,我们尝试把除了\(5\)之外的左边的数字移动到右边,那么有多少种方案?
首先在这\(n-2\)个数字当中,5不能右移过去,那也就是剩下\(n-3\)个数字,那么此时枚举往右放多少个数字,放\(0,1,2,3,...,n-3\)都是可以的,所以我们要对答案乘上:
\[
C_{n-3}^0+C_{n-3}^1+C_{n-3}^2+...+C_{n-3}^{n-3}=2^{n-3}
\]
综上所述,答案为:
\[
C_m^{n-1}\times (n-2)\times 2^{n-3}
\]
code
Codeforces 1312D. Count the Arrays
标签:count 有一个 最大的 mat The 就会 理解 isp ubuntu
原文地址:https://www.cnblogs.com/zxytxdy/p/12453064.html