标签:顺序 它的 strong cti 直接 静态 time 变量 sea
有如下三种作用域的变量:
局部变量
每个函数(函数会在后面细讲)中定义的变量,只能在当前函数体内访问到。
全局变量
在函数体中用global关键字声明的变量,它的作用域是:所有的函数和Matlab工作空间。任何一个地方改变了全局变量的值,其他所有使用到它的地方的值都会随着改变。建议尽量少使用全局变量。
静态变量
在一个函数中可以使用persistent关键字声明一个静态变量,只要函数存在,静态变量就不会被清除。
Matlab的控制流也与c/c++大体相同,唯一要注意的是每个条件都有相应的end关键字。
示例:
新建脚本文件,保存为exe1_1
x=input(‘enter‘‘x‘‘:‘);%input函数返回你输入的整数,提示信息用‘‘括起来,如果想要输出单引号,两个单引号‘‘ ‘‘即可 if(x>0) y=1; elseif(x==0) y=0; else y=-1; end %不要忘记加end,Matlab不会自动补全end,最好一开始就写下来,养成良好的编程习惯至关重要 disp(y) %disp作为输出函数
在命令行窗口调用exe1_1,输入-5
得到结果:
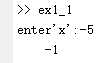
示例:新建脚本文件,保存为ex1_2
month=3;
switch month
case {3,4,5}
season=‘spring‘
case {6,7,8}
season=‘summer‘
case {9,10,11}
season=‘autumn‘
otherwise
season=‘winter‘
end
得到结果:
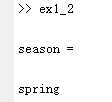
注意
1.M文件的搜索路径必须与当前路径一致,否则运行会出错,搜索路径即保存M文件的位置。可以直接修改当前路径与搜索路径一致,也可以添加搜索路径,这样就一劳永逸了。

2.如果遇到不认识的函数,可以利用help/doc命令在命令行查找,格式为help/doc function,function为函数名,养成查阅文档的习惯很重要!
sum = 0;
for i = 1 : 100
sum = sum + i;
end
disp(sum)
5050
i = 1;
sum = 0;
while i <= 100
sum = sum + i;
i = i + 1;
end
disp(sum)
5050
范例:
使用0.618法(黄金分割法)极小化f(t)=exp(-t)+exp(t),区间为[-1,1]。(即逼近函数在已知区间的极小值,找到对应的t
0.618法主要思想:
0.618法在给定区间[a,b]内适当插入两点a1,a2,并计算其函数值。
a1,a2将区间分成三段,通过函数值大小的比较,删去其中一段,使搜索区间得以缩小,
然后再在保留下来的区间上作同样的处理,如此迭代下去,从而得到极小点的数值近似解。
0.618法主要步骤:
1.在区间[a,b]内分别按照0.618和0.382的比例处取点a1 ,a2, 把[a,b]分为三段。
2.如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+0.618*(b-a)
3.如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=a+0.382*(b-a)
4.如果满足迭代条件或者超出给定迭代次数,程序终止,否则继续运行下去。
新建名为fai.m的函数和zero_soe.m的函数
1 function z= fai(t) 2 % fai函数 3 % 给定函数 4 z=1*exp(-t)+1*exp(t); 5 end
1 function [k] = zero_soe(a0,b0,iter,tol) 2 %UNTITLED3 精确线性搜索之0.618法 3 % a0,b0分别代表左端点,右端点 4 % iter代表给定的迭代次数 5 % tol代表误差限 6 m=a0+0.382*(b0-a0); %试探点lameda0 7 n=a0+0.618*(b0-a0); %试探点u0 8 ym=fai(m); 9 yn=fai(n); 10 count=0; %现有的迭代次数 11 while(count<iter) 12 if(ym>yn) 13 if(b0-m<=tol) 14 k=n; 15 return; 16 else 17 a0=m; 18 m=n; 19 ym=yn; 20 n=a0+0.618*(b0-a0); 21 yn=fai(n); 22 count=count+1; 23 end 24 else 25 if(n-a0<=tol) 26 k=m; 27 return; 28 else 29 b0=n; 30 n=m; 31 yn=ym; 32 m=a0+0.382*(b0-a0); 33 ym=fai(m); 34 count=count+1; 35 end 36 end 37 end 38 if(count>=iter) 39 disp(‘迭代次数超过给定次数!‘) ; 40 end 41 end
得到结果:
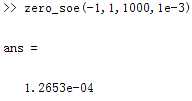
通过求导可知函数的极小值对应的t等于0,可知极小化的结果是正确的。
当程序发生异常时,需要捕获异常并对异常进行处理,这个时候需要用到try-catch语句,基本语法格式:
try
语句块1
catch
语句块2
end
% 如果语句块1发生异常,会跳到语句块2
在任意代码段的开始和结束使用tic和toc语句对,可以计算这段代码的用时,编写一个名为myadd.m的m函数如下:
function sum = myadd()
tic
s = 0;
for i = 1:1000000
s = s + 1/i;
end
sum = s;
toc
在命令行中调用myadd函数:
?myadd
elapsed_time =
1.1740
ans =
14.3927
可以看到myadd函数用时1.174秒,结果为14.3927
向量化的操作相比循环操作而言,在数据量大的时候性能将会显著提高。
比如对比如下两个函数:
function result = myadd1()
tic
s = 0;
for i = 1:1000000
s = s + 1/i;
end
result = s;
toc
function result = myadd2()
tic
i = 1:1000000;
result = sum(1./i);
toc
分别调用myadd1、myadd2函数,结果对比如下:
myadd1
elapsed_time = 1.1740
ans = 14.3927
myadd2
elapsed_time = 0.0200
ans =14.3927
可以看出,采用向量化的操作后,相比使用循环,同样的数据量的计算效率得到了几十倍的提升。
可以防止损耗过多程序性能。
先使用zeros或ones函数对大型矩阵预先定维,将会显著降低程序耗时。
标签:顺序 它的 strong cti 直接 静态 time 变量 sea
原文地址:https://www.cnblogs.com/xxfx/p/12460598.html