标签:double 思路 print font mamicode query 区间 min 矩阵
迅哥讲解(说实话没有认真听,不过关系不大)
RMQ:Range Minimum Maximum Query 给定一个序列A[1…N],问A[i…j]之间的极值 如果只问一次,
显然是O(N) 标准RMQ问题是:不停的查询同一个序列上的不同区间内的极值
序列A的长度N,一共Q次查询 纯暴力法:O(NQ) 带预处理的暴力法: 矩阵B[N][N],
令B[i][j]是A[i…j]的极值 求B需要一个双重循环,O(N2) 对每一次查询只需O(1)即可
所以总时间复杂度O(N2+Q) 空间复杂度则为O(N2)
Sparse Table算法
矩阵M[N][logN+1] M[i][j]是区间A[i, i+2j)的极值 矩阵M的元素值的确定:
类似于倍增算法
本题采用的倍增的思路 (说实话感觉像个dp)
首先令M[i][j]代表从i开始长度为2^j的数列 中的极值(左闭右开的区间)
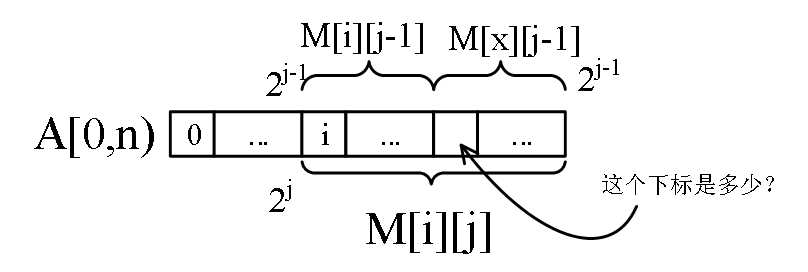
由此图可知 找寻极值之时只要查找左右两个区间就行了(有点二分的意味)
所以输入的原始值就是M[i][0] 而每一次找寻的过程中就是M[i][j]=极值(M[i][j-1],M[i+2^(j-1)][j-1]) 只要从2^j开始例举,
但是注意因为i是从1开始,而最少j=1,所以i的值小于等与n-1,并非n。
拿迅哥原图说话
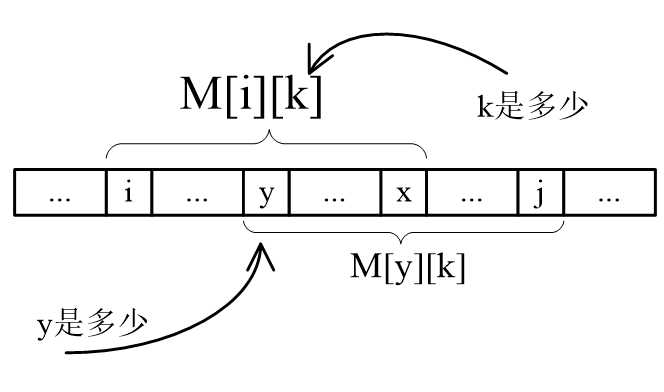
给定两个下标l,r进行查询,我的k是从0开始的,所以相等时也要再+1,
查找从i开始长度为2^k和从r-2^k+1长度为2^k;
只不过可以直接求取( k = (int)( log((double)(r-l+1)) / log(2.0) );)
贴代码
#define ll int using namespace std; const int maxn=1e5+7; int n; int M[maxn][1050]; void st_RMQ() { for (int j=1;(1<<j)<=n;++j) for (int i=0;i+(1<<j)-1<=n;++i) M[i][j]=max(M[i][j-1],M[i+(1<<(j-1))][j-1]); } int RMQ(int l,int r) { int k=0; while ((1<<(k+1))<=r-l+1) ++k; return max(M[l][k],M[r-(1<<k)+1][k]); } int main() { int t; cin>>n>>t; for (int i=1;i<=n;++i) cin>>M[i][0];///以i开头长度为1中的最大值 st_RMQ(); int x,y; while(t--) { scanf("%d%d",&x,&y); printf("%d\n",RMQ(x,y)); } return 0; }
标签:double 思路 print font mamicode query 区间 min 矩阵
原文地址:https://www.cnblogs.com/qimang-311/p/12483454.html