标签：ima   频率   电动   微分方程   http   参数   mamicode   数学   输出   

1 控制系统的数学模型

数学模型是描述系统输入量、输出量以及内部各变量之间关系的数学表达式，揭示了系统结构及其参数与其性能之间的内在关系。

静态数学模型：静态条件（变量各阶导数为零）下描述变量之间关系的代数方程。反映系统处于稳态时，系统状态有关属性变量之间关系的数学模型。

动态数学模型：描述变量各阶导数之间关系的微分方程，描述动态系统瞬态与过渡态特性的模型。也可定义为描述实际系统各物理量随时间演化的数学表达式。微分方程或差分方程常用作动态数学模型。

对于给定动态系统，数学模型表达不唯一。工程上常用的有：微分方程，传递函数和状态方程。不过对于线性系统，它们之间是等价的。

2 建立数学模型的方法

1. 解析法

依据系统及元件各变量之间所遵循的物理规律写出相应的数学关系式，建立模型。

2. 实验法

人为地对系统施加某种测试信号，记录其输出响应，并用适当的数学模型进行逼近，这种方法也称为系统辨识。

3 数学模型的形式

1. 时间域

• 微分方程
• 差分方程
• 状态方程（一阶微分方程组）

2. 复数域

• 传递函数
• 结构图

3. 频率域

• 频率域

4 建立数学模型的一般步骤

用解析法列写系统或元件微分方程的一般步骤是：

1. 分析系统工作原理和信号传递变换过程，确定系统和各元件的输入、输出量。
2. 从系统输入端开始，按照信号传递变换过程，依据各变量所遵循的物理学定律，依次列写各元件、部件的动态微分方程。
3. 消去中间变量，得到一个描述元件或系统输入、输出变量之间关系的微分方程。
4. 写成标准化形式。与输入有关项放在等式右侧，与输出有关项放在等式左侧，且各阶导数项按降幂排列。

5 控制系统微分方程的列写

5.1 机械系统

在机械系统中，有些构件惯性和刚度较大，有些构件惯性较小、柔度较大。

我们将前者的弹性忽略视其为质量块，将后者的惯性忽略视其为无质量弹簧。

这样，机械系统便可以抽象为质量-弹簧-阻尼系统。

1. 质量

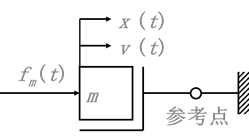
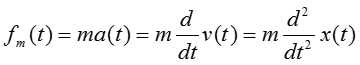
2. 弹簧

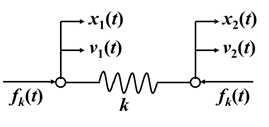
3. 阻尼

5.1.1 机械平移系统

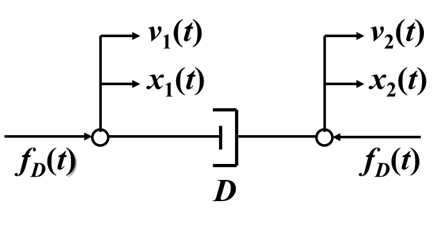
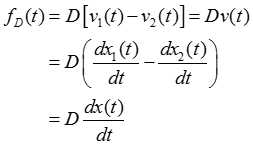
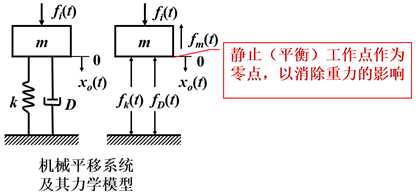
列出各元件的动态微分方程：

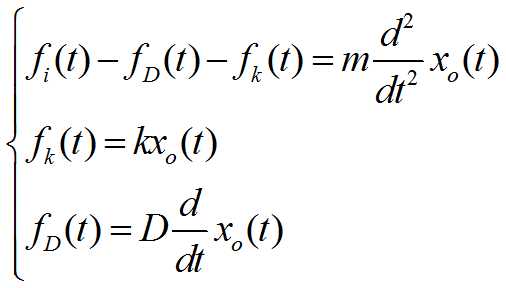
消去中间变量并写成标准形式：

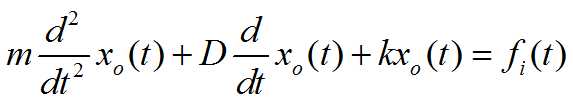
式中，m、D、k通常均为常数，故机械平移系统可以由二阶常系数微分方程描述。

微分方程的系数取决于系统的结构参数，而阶次等于系统中独立储能元件（惯性质量、弹簧）的数量。

5.1.2 机械旋转系统

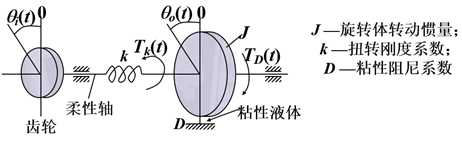
列出各元件的动态微分方程：

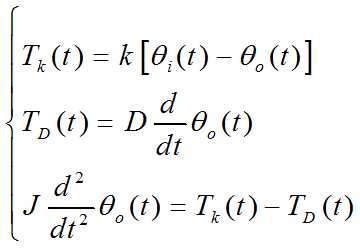
消去中间变量并写成标准形式：

5.2 电路系统

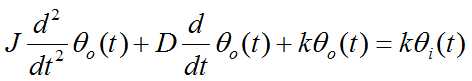
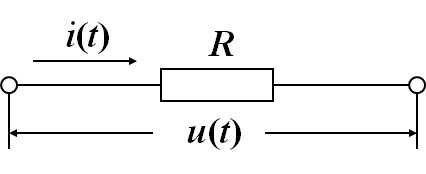
电路系统包含三个基本元件：电阻、电容和电感。

1. 电阻

2. 电容

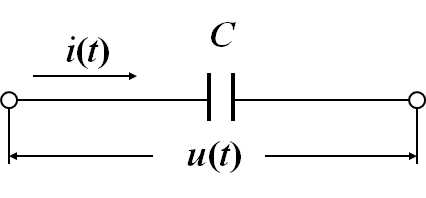
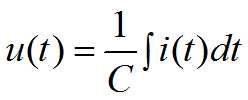
3. 电感

5.2.1 R-L-C无源电路网络

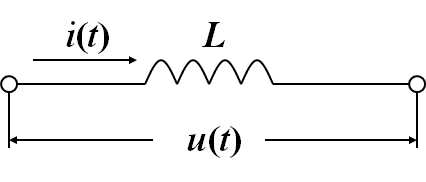
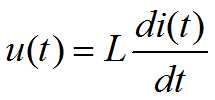
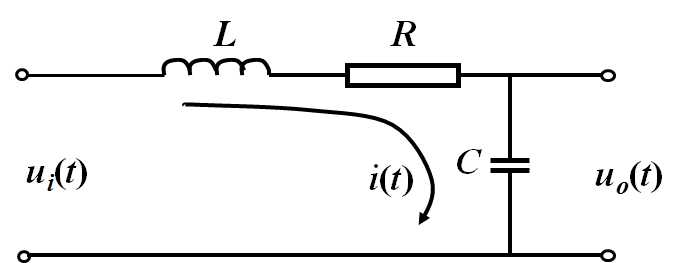
列出各元件的动态微分方程：

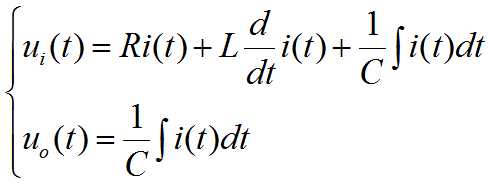
消去中间变量并写成标准形式：

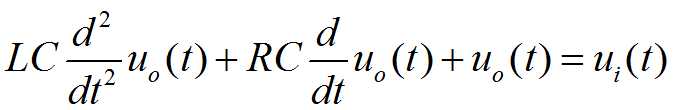
一般R、L、C均为常数，上式为二阶常系数微分方程。

若L=0，则系统可简化为：

5.2.2 有源电路网络

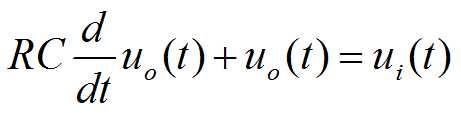
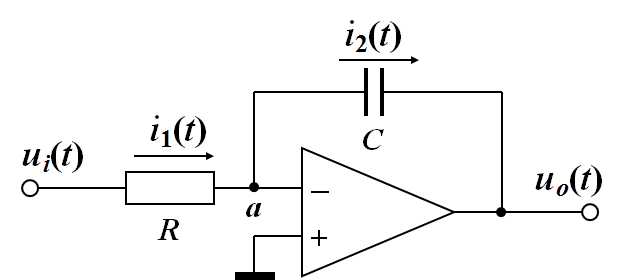
列出各元件的动态微分方程：

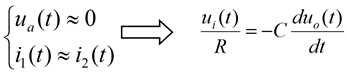
消去中间变量并写成标准形式：

5.3 电磁系统

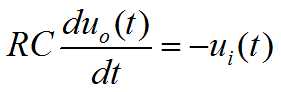
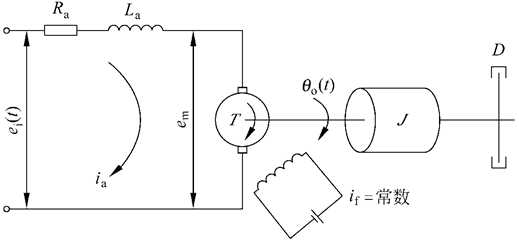
列出各元件的动态微分方程：

磁场对载流线圈作用的定律：

基尔霍夫定律：

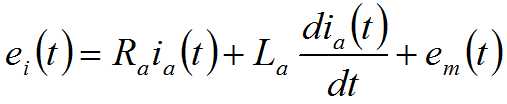
电磁感应定律：

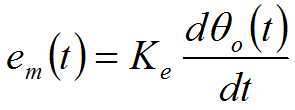
牛顿第二定律：

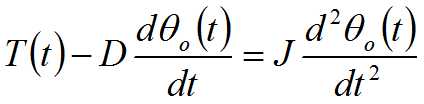
消去中间变量并写成标准形式：

上式为电枢控制式直流电动机的控制系统的动态数学模型。

当电枢电感较小时，通常可忽略不计，系统微分方程可简化为：

6 小结

1. 物理本质不同的系统，可以有相同的数学模型，从而抛开系统的物理属性，用同一方法进行具有普遍意义的分析研究（信息方法）。

2. 从动态性能看，在相同形式的输入作用下，数学模型相同而物理本质不同的系统其输出响应相似（相似系统是控制理论中进行实验模拟的基础）。

3. 通常情况下，元件或系统微分方程的阶次等于元件或系统中所包含的独立储能元件的个数。

4. 系统的动态特性是系统的固有特性，仅取决于系统的结构及其参数，与系统的输入无关。

控制工程数学模型

标签：ima   频率   电动   微分方程   http   参数   mamicode   数学   输出   

原文地址：https://www.cnblogs.com/yangmi511/p/12486981.html