标签:ade 表示 include main 出现 训练 多重 str 内存
Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。
当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。
说明:在本题中,答案是要求Fn除以10007的余数,因此我们只要能算出这个余数即可,而不需要先计算出Fn的准确值,再将计算的结果除以10007取余数,直接计算余数往往比先算出原数再取余简单。
#include<iostream> using namespace std; int fibo(int n) { if(n==1||n==2) return 1; else { return fibo(n-1)+fibo(n-2); } } int main() { int x; while(cin >> x) { cout << fibo(x)%10007 << endl; } return 0; }
用递归的方法来做发现超时了!!!
以递归求解的过程中会出现很多重复求解 如图:
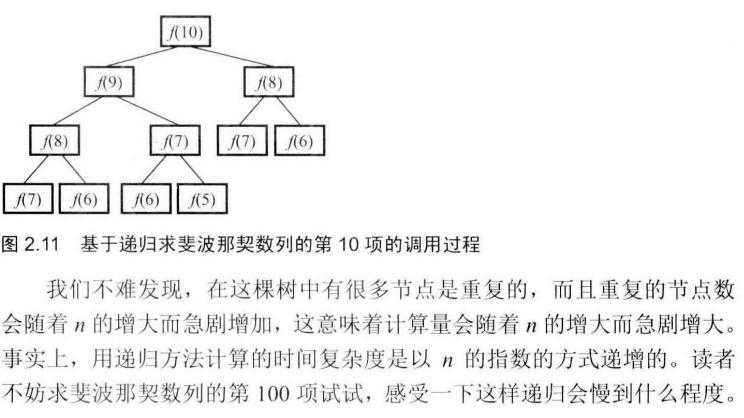
优化方法:
#include<iostream> using namespace std; long fib(long n) { if(n==1||n==2) return 1; else { long f1=1; long f2=1; long f=0; for(int i=3;i<=n;i++) { f=(f1+f2)%10007; f1=f2%10007; f2=f%10007; } return f; } } int main() { long x; while(cin >> x) { cout << fib(x) << endl; } return 0; }
或者
#include <iostream> using namespace std; int main() { int n; cin>>n; long long a[n]; a[0] = 0,a[1] = 1; //直接使用迭代这样的话时间复杂度为O(n),这样的话不会超时,但是如果n大的话,空间复杂度会更大,以空间换时间 for(int i=2;i<=n;i++){ a[i] = (a[i-2]+a[i-1])%10007; } cout<<a[n]<<endl; return 0; }
标签:ade 表示 include main 出现 训练 多重 str 内存
原文地址:https://www.cnblogs.com/wlyperfect/p/12488597.html