标签:zoom 思想 关联 inf 集中 res 机器 度量 取值
本来还是想像以前一样,继续学习《 Python数据挖掘入门与实践 》的第三章“决策树”,但是这本书上来就直接给我怼了一大串代码,对于决策树基本上没有什么介绍,可直接把我给弄懵逼了,主要我只听过决策树还没有认真的了解过它。
这一章节主要是对决策树做一个介绍,在下一个章节,将使用决策树来进行预测分类 。
Decision Tree是一类较为常见的机器学习的方法。它既可以作为分类算法,也可以作为回归算法。
如何来介绍决策树,这里举一个例子:在大学,你找女朋友的时候,心目中顺序应该是这样的(仅仅是举一个例子):
为了更好的表示上面的这一些问题,我们可以将其画成一张树状图如下所示:

上面的这棵树就是我们找女朋友的决策过程,圆角矩形代表了判断条件,椭圆形代表了决策结果。通过性别,年龄,专业这几个属性,最终我们得出了最终的决策。而这棵树也就被称之为决策树。
大家通过上图会发现有3个东西:
在一棵决策树中,包含了一个根节点,多个内部节点(判断条件) 和若干个叶子节点。先说叶子节点,在决策树中,叶子节点对应了决策结果,决策结果可以有多种类型(图中是yes和no,也可以为1,2,3)。内部节点和根节点对应的都是属性测试,只不过先后顺序不同。
总的来说,决策树体现的是一种“分而治之”的思想,
那么这里就有一个问题,谁来当根节点?谁又来当中间的节点?先后顺序又是怎样的?(这里先不说算法流程,从简单开始说起,然后再说算法流程)
首先我们需要明白根节点和中间节点是不同的,一个是统领全局的开始包含所有的样本。一个是负责局部的决策,并且随着决策树的不断的进行决策,所包含的样本逐渐属于同一个类别,即节点的“纯度”越来越高。
那么,我们如何来寻找合适根节点(也就是属性)呢?靠感觉?靠感觉当然不行,我们需要一个具体的数值来决定,很幸运,香农帮助我们做到了。
“信息熵”(information entropy):可以度量样本集合中的“纯度”。 在信息世界,熵越高,表示蕴含越多的信息,熵越低,则信息越少。 而根节点需要包含所以的样本,则根结点的熵最大。
设样本集合为\(D\),第\(k\)类样本所占比例为\(p_k(k = 1,2,3,……n)\),则集合\(D\)的信息熵为:
\[ Ent(D) = - \sum_{k=1}^{n}p_klog_2p_k\Ent(D)越大,则D的纯度越小,也就是说集合D越混乱。 \]
现在,我们已经知道一个集合\(D\)中的信息熵是多少,那么我们如何来进行划分呢?首先,我们需要明确一个划分的标准(也就是目标),我们当然希望划分之后,划分之后的集合的熵越来越小,也就是划分后的集合越来越纯,这里我们引入信息增益这个概念。
下面是西瓜书中对信息增益的定义:
假设离散属性\(a\)有\(V\)个可能的取值\(\{a^1,a^2,a^3……a^V\}\),若以属性\(a\)对样本进行划分,则有V个分支,其中第\(v\)个分支包含了\(D\)中在属性\(a\)上取值为\(a^v\)的样本,记为\(D^v\)。我们可以计算出\(D^v\)的信息熵,然后考虑到不同分支结点的样本数不同,给分支结点赋予权重\(\frac{|D^v|}{|D|}\),样本数愈多,则影响力越大,则可以计算出属性\(a\)对样本集\(D\)进行划分的“信息增益”:
\[ Gain(D,a) = Ent(D) - \sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v) \]
一般来说,信息增益越大,则代表划分后的集合越“纯”,也就是说使用\(a\)属性来划分的效果最好,那么我们就可以使用\(a\)属性来进行划分。ID3算法就是使用信息增益来作为标准划分属性的。
下面是来自《西瓜书》的决策树生成算法流程:

决策树生成是一个递归的过程,在下面3中情况中,递归会返回:
算法可能不是那么的形象好理解,下面将以实际的例子来展示。
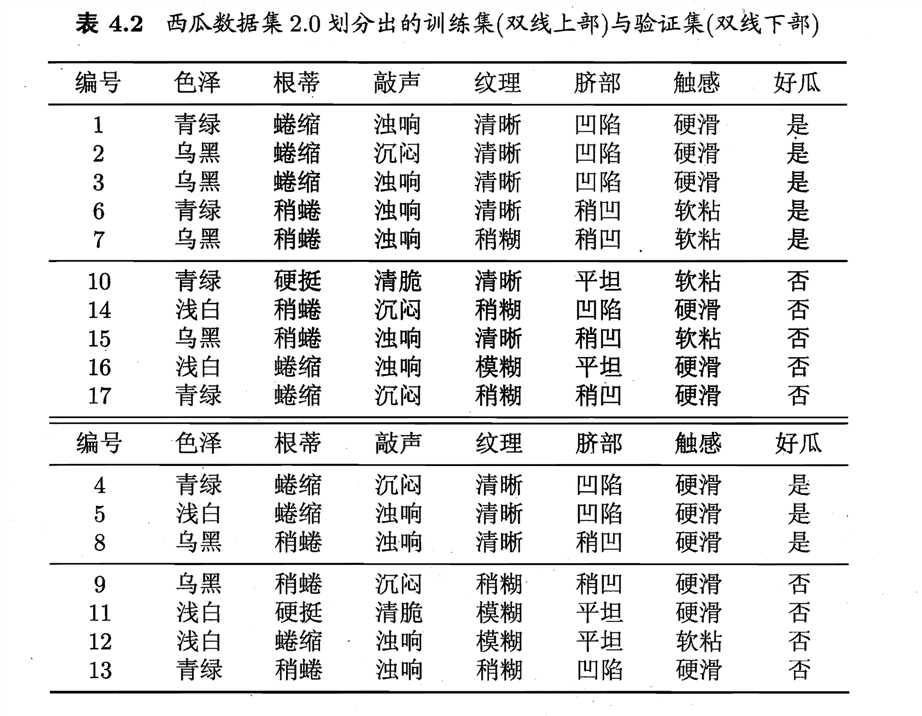
在最上面上面的找女朋友的例子并不是特别的好,属性太少。这里以西瓜书中的??来进行举例。这个属性还是挺多的。
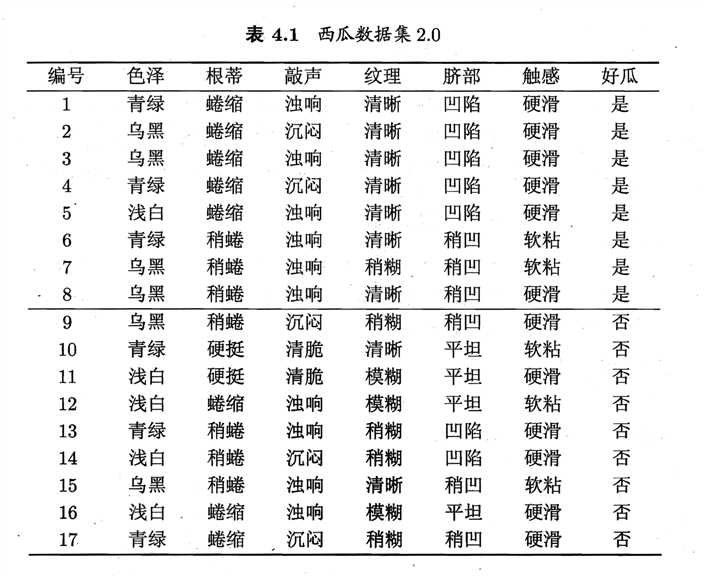
在上图中,属性的集合是{色泽,根蒂,敲声,纹理,脐部,触感}(目前不考虑编号这个属性),分类的集合是{是,否},一共有17个样本。
首先让我们来及计算集合\(D\)的熵值。在集合\(D\)中,好瓜(是)占\(p_1 = \frac{8}{17}\),坏瓜(否)占\(p_1 = \frac{9}{17}\),所以集合\(D\)的熵为:
\[
Ent(D) = -\sum_{k=1}^2p_klog_2p_k = -(\frac{8}{17}log_2\frac{8}{17} + \frac{9}{17}log_2\frac{9}{17}) = 0.998
\]
以色泽作为划分标准,可以得到3个子集:
\[
D^1(色泽=青绿) = \{1,4,6,10,13,17\} \ 在D^1中p_1 = \frac{3}{6},p_2=\frac{3}{6}\ D^2(色泽=乌黑) = \{2,3,7,8,9,15\}\ 在D^2中p_1 = \frac{4}{6},p_2=\frac{2}{6}\ D^3(色泽=浅白) = \{5,11,12,14,16\}\ 在D^2中p_1 = \frac{1}{5},p_2=\frac{4}{5} \ 其中集合中的数字代表表格中的编号
\]
我们可以获得\(D^1,D^2,D^3\)的信息熵:
\[ Ent(D^1)=-(\frac{3}{6}log_2\frac{3}{6}+\frac{3}{6}log_2\frac{3}{6}) = 1.00 \Ent(D^2)=-(\frac{4}{6}log_2\frac{4}{6}+\frac{2}{6}log_2\frac{2}{6}) = 0.918 \Ent(D^3)=-(\frac{1}{5}log_2\frac{1}{5}+\frac{4}{5}log_2\frac{4}{5}) = 0.722 \\]
因此色泽的信息增益为:
\[
\begin{equation}
\begin{aligned}
Gain(D,色泽) &= Ent(D) - \sum_{v=1}^3\frac{|D^v|}{|D|}Ent(D^v)\&= 0.99 - (\frac{6}{17}\times 1.00 + \frac{6}{17}\times0.918 +\frac{5}{17}\times0.722) \&= 0.109
\end{aligned}
\end{equation}
\]
同理可以得到:
\[
\begin{equation}
\begin{split}
& Gain(D,根蒂) = 0.143;Gain(D,敲声) = 0.141;\& Gain(D,纹理) = 0.381;Gain(D,脐部) = 0.289; \& Gain(D,触感) = 0.006;Gain(D,色泽)=0.109;
\end{split}
\end{equation}
\]
通过计算可以得到,纹理的信息增益最大,因此他被选为划分的属性如下图:
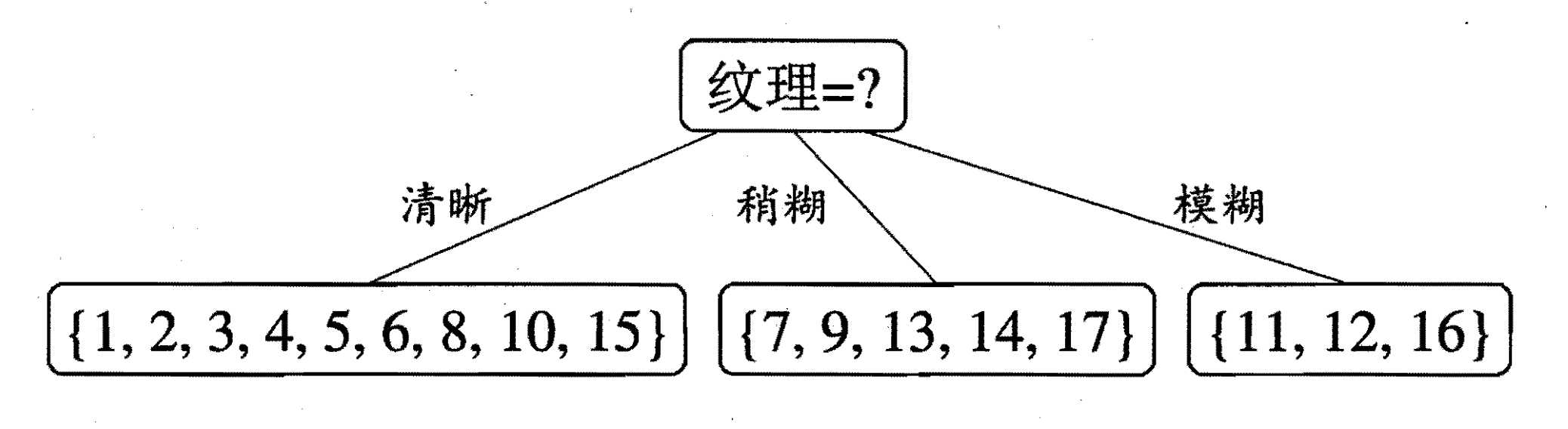
然后以纹理是“清晰为例”,该集合\(D^1=\{1,2,3,4,5,6,8,10,15\}\),可用的属性集合为{ 色泽,根蒂,敲声,脐部, 触感}。因此,基于\(D^1\)又可以计算出各个属性的信息增益:
\[ \begin{equation} \begin{split} & Gain(D^1,色泽) = 0.043;Gain(D^1,根蒂) = 0.458;\&Gain(D^1,敲声) = 0.331; Gain(D^1,触感) = 0.458;\&Gain(D^1,脐部)=0.458; \end{split} \end{equation} \]
因此我们可以在“根蒂”,“触感”,“脐部”中任意选择其中一个作为划分属性。最终得到以下的决策树:
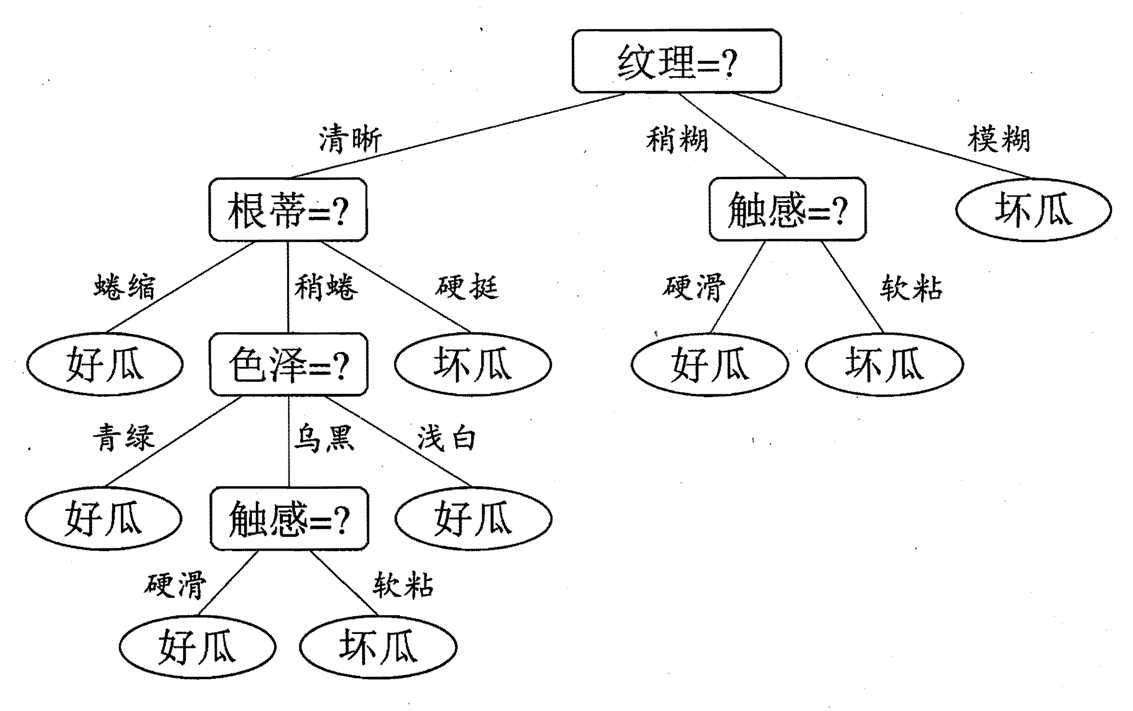
通过上面的这些步骤,我们就得到了一颗关于西瓜的好坏的决策树。ID3算法就是用信息增益作为划分标准。
上面的例子来自西瓜书,以及计算的结果也来自西瓜书。
在这里有一个问题,\(Gain(D,属性)\)越大,就一定能够作为划分标准吗?假如它是一个无用的属性呢?比如上图中编号这个属性,如果在上面我们选择编号作为根节点,那么第一次划分就能够得到17个集合,每一个集合只有1个样本,\(Gain(D,编号)\)必定能够达到最大值。但是我们知道,编号这个属性在这里是毫无作用的。如果将这个问题进行泛化,如果一个属性在分类中起到的作用给很小(也就是它对分类的影响很小),那么我们应该怎么考虑呢?
这里我们可以使用增益率来作为划分的标准,定义如下
\[
\begin{equation}
\begin{split}
&Gain\_ratio(D,a) = \frac{Gain(D,a)}{IV(a)} \&其中\&IV(a) = -\sum_{v=1}^V\frac{D^v}{D}log_2\frac{D^v}{D}
\end{split}
\end{equation}
\]
\(IV(a)\)称之为属性\(a\)的固有值(intrinsic value),属性\(a\)的可能取值越多(划分的\(D^v\)的集合越多),\(IV(a)\)就会越大。若像编号一样进行划分(每一个划分的集合中只有一个样本),随着编号的增多,\(IV(a)\)的取值如下图:
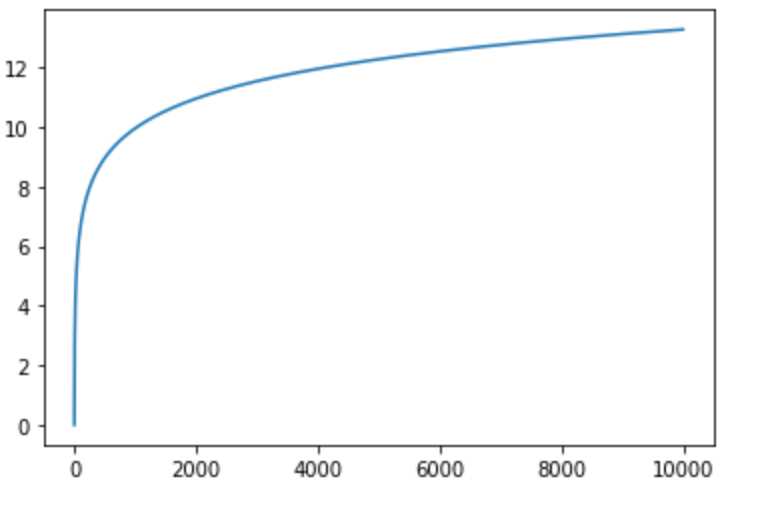
其中著名的C4.5算法就是使用增益率来划分属性。
除了这种解决方案,还有一种解决方法,基尼指数作为划分标准,CART决策树使用这种方法。
前面我们使用信息熵来表示集合的纯度,这里我们使用基尼值来表示:
设样本集合为\(D\),第\(k\)类样本所占比例为\(p_k(k = 1,2,3,……n)\)
\[
\begin{equation}
\begin{aligned}
Gini(D) &= \sum_{k=1}^{|n|}\sum_{k'\neq k}p_kp_{k'}\&=1 - \sum_{k=1}^{|n|}p_k^2
\end{aligned}
\end{equation}
\]
\(Gini(D)\) 反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。因此, $Gini(D) $越大,则数据集越复杂,纯度越低。
同样,属性\(a\)的基尼指数定义为:
\[ Gini\_index(D,a) = \sum_{v=1}^V\frac{D^v}{D}Gini({D^v}) \]
因此,在我们选择合适的属性进行划分的时候,选择划分后基尼指数较小的属性作为划分标准即可。
这个时候我们再来看一看这幅图,应该就看的懂了吧。

首先,我们先说一下剪枝的目的——防止“过拟合”。在决策树的学习过程中,为了保证正确性,会不断的进行划分,这样可能会导致对于训练样本能够达到一个很好的准确性,但是对于测试集可能就不是很好了,这样的模型不具备泛化性。下面来举一个例子:
我们有如下的数据集:
坐标轴的上的每一个点代表一个样本,有\(x,y\)两种属性,其中,蓝色的点代表类0,橙色的点代表类1。
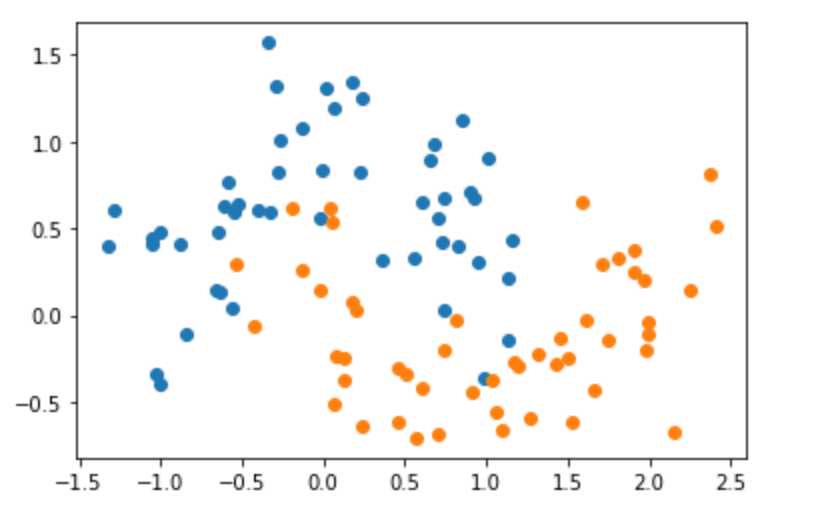
当我们使用决策树进行训练后,模型对于数据的识别区域如下,在粉红色区域,其认为里面的点为类0,蓝色的区域为类1:
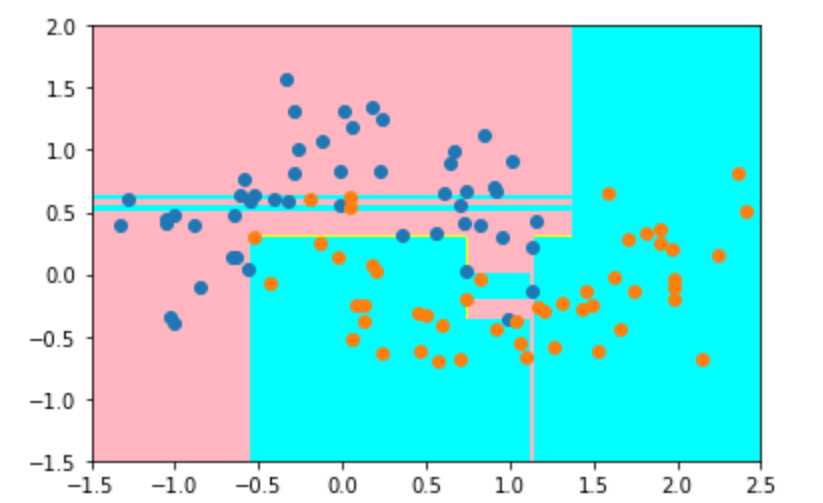
大家可能发现一个问题,那就是这个区域划分的太“细致”了。因为数据是有噪音(noise)的,这样划分明显是不合理的。这里大家可以看一看决策树的图片:
.png)
那么如何来缓解这种问题呢?其中有一种方法就是去掉一些分支(剪枝)来降低过拟合的风险。
剪枝有两种方案:
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
用通俗的话来说,就是如果进行划分能够带来更好的结果就进行划分,否则不进行划分。首先,我们定义一个训练集和一个验证集如下:(西瓜书中间的例子)
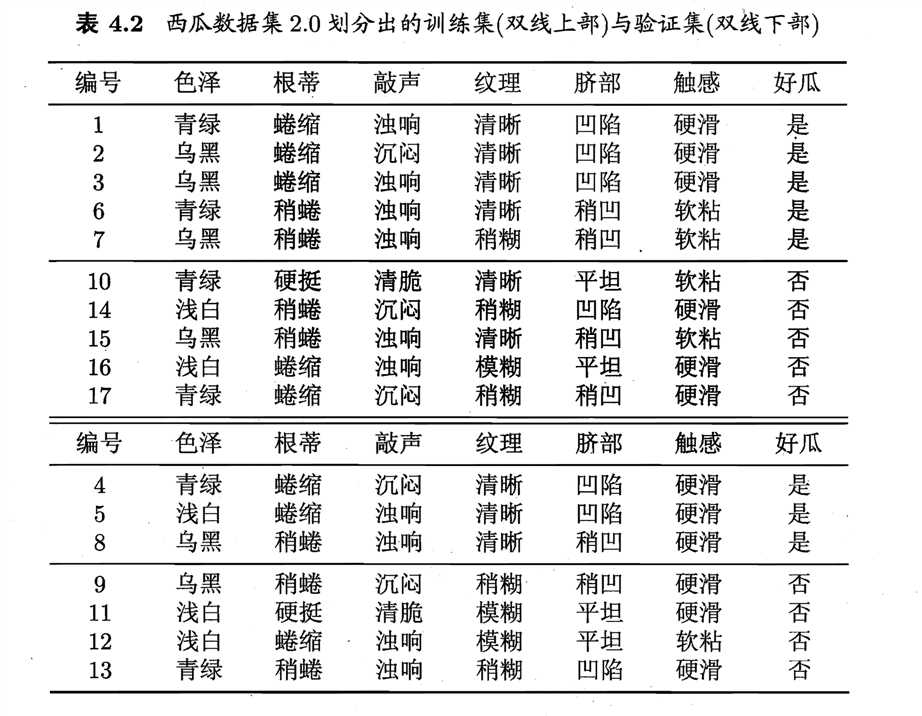
上面一部分是训练集,下面一部分是测试集。然后让我们来对训练集(记住是训练集)进行划分,划分的规则与上面的一样。
下面的这幅图是未剪枝的情况。
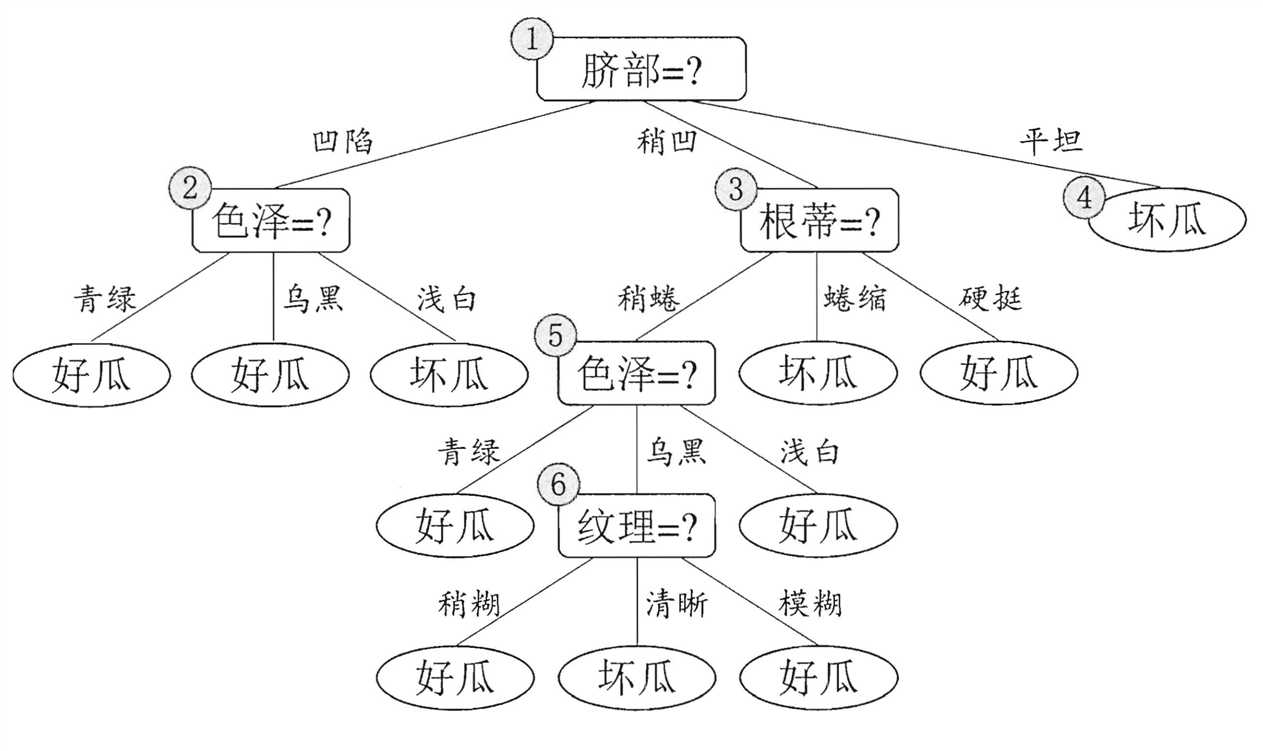
那么,剪枝是如何进行的呢?
首先,我们先判断“脐部”,如果我们不对“脐部”进行划分,也就是说这棵决策树是这样的:
只有一个好瓜的判断结果(根据上面的算法流程图,node节点直接就是叶子节点,其类别由样本中最多的决定【这里既可以是好瓜也可以是坏瓜,因为数量一样】)

这样下来,也就是说无论你什么瓜过来我都判断它是好瓜。使用验证集进行验证,验证的精准度为:\(\frac{3}{7} \times100\% = 42.9\%\)。如果进行划分呢?
下图便是进行划分的情况,其中被红色圆圈框出来的部分表示验证正确。
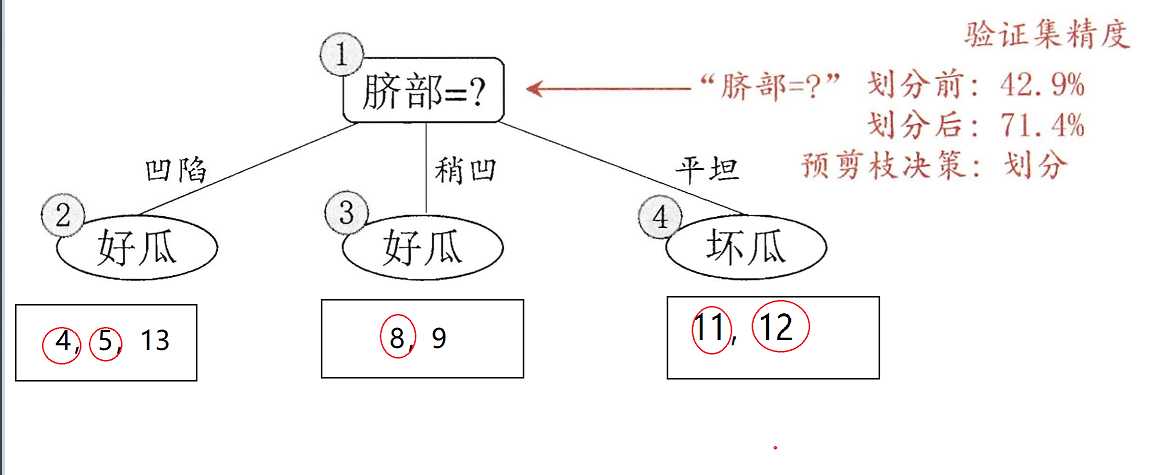
如果只划分“脐部”这个属性,我们可以通过其来划分好瓜和坏瓜,通过验证机去测试,我们可以得到划分后的准确性为:\(\frac{5}{7}\times100\%=71.4\% > 42.9\%\),所以选择划分。
下面便是进行前剪枝后的划分结果,使用验证集进行验证,精度为\(71.4\%\)
尽管该方案可以降低过拟合的风险,并在一定程度上能够降低算法的复杂度,但也会带来欠拟合的风险。因为会出现另外一种情况:有可能当前划分不能提升泛化能力,但是在此基础上的后续的划分也许可以导致性能显著提高。
后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点.
后剪枝和前剪枝的不同在于后剪枝是在生成决策树后再进行剪枝。顺序是由下到上。
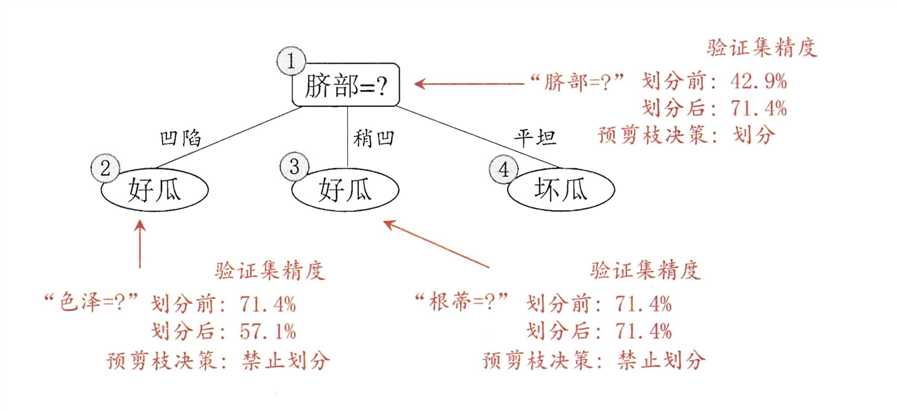
我们继续来看这幅图:
通过验证集,我们易得到该决策树的识别率为\(42.9\%\)。
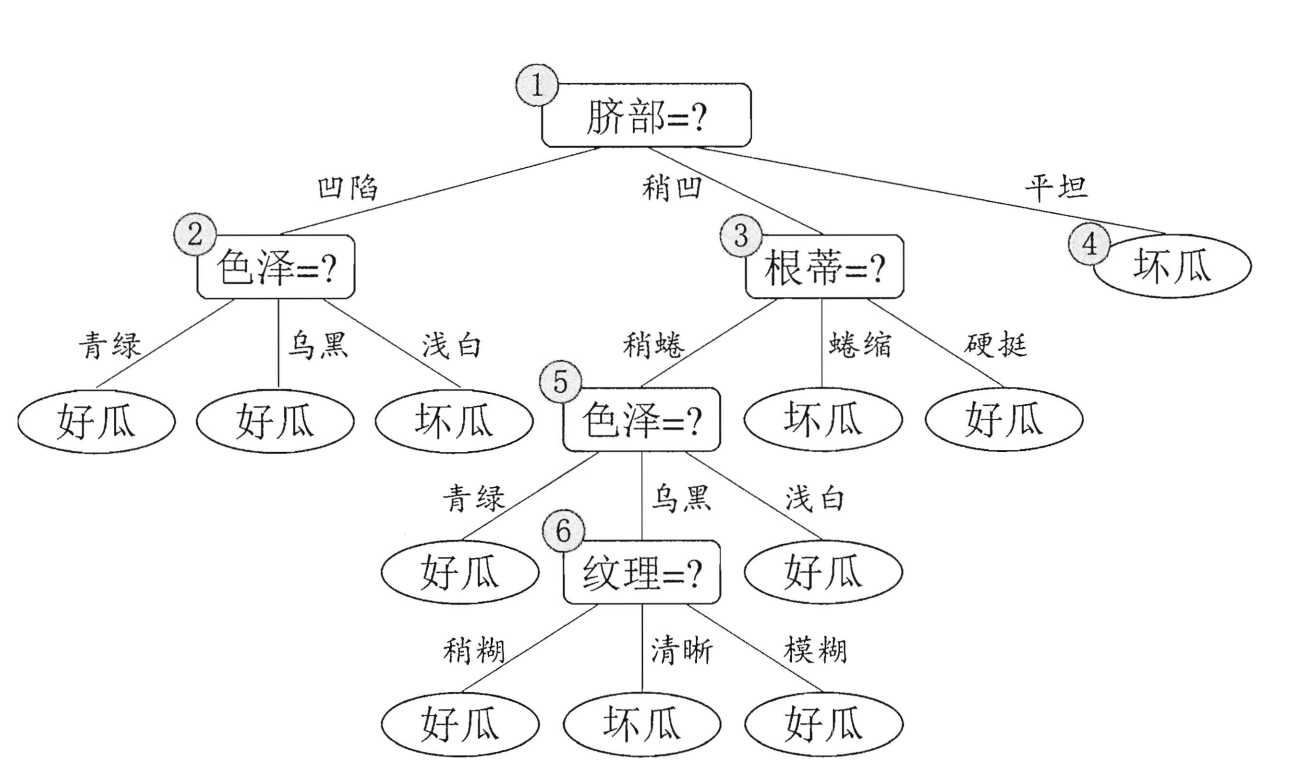
让我们重新看一下数据吧,数据集和验证集如下:
现在让我们来进行剪枝吧!!首先先看节点⑥,节点6中包含编号为\(\{7(好瓜),15(坏瓜)\}\)的训练样本,因此我们将节点⑥变成叶节点并标记为“好瓜(坏瓜也ok)”。如下所示:
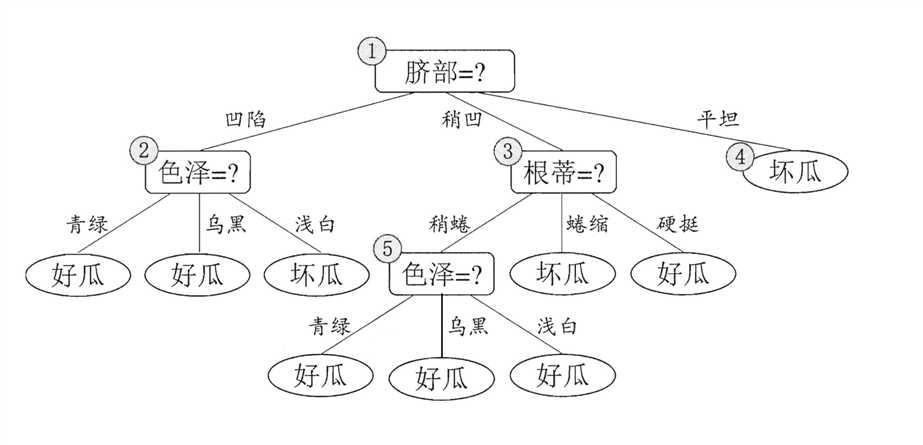
在这种情况下,验证集中序号为\(\{4,8,11,12\}\)验证正确,精度调高到\(\frac{4}{7} \times 100\%= 57.1\%\),因此可以进行剪枝。
考虑结点⑤,包含编号为\(\{6,7,15\}\),将其变成叶节点(标记为“好瓜”),使用验证集去验证,其精度仍为\(57.1\%\),没有提高,进行考虑。同理可得到下面的这副图片:
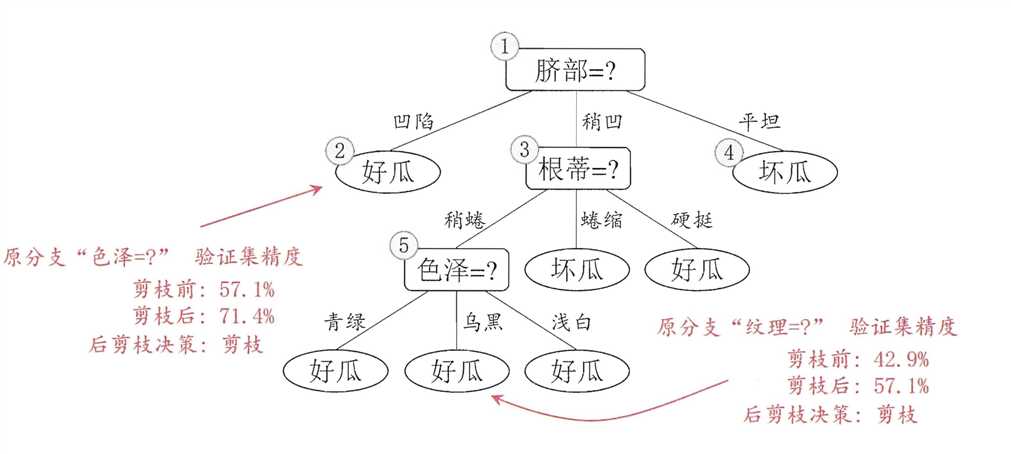
最终,该决策树的精度为\(71.4\%\)
比较预剪枝和后剪枝,后剪枝保留的分支更多,同时后剪枝的欠拟合的风险很小,泛化性能往往优于预剪枝决策树,但是显而易见,训练的时间要比预剪枝大得多。
什么是随机森林呢?随机森林是一个包含多个决策树的分类器,由很多决策树构成,不同的决策树之间没有关联。当我们进行分类任务时,森林中的每一棵决策树都会分别对样本进行判断和分类,每个决策树会得到一个自己的分类结果,决策树的分类结果中哪一个分类最多,那么随机森林就会把这个结果当做最终的结果。 (emm,少树服从多树)。好像很简单的样子,但是这里有一个问题,那就是随机森林中有多个决策树,那么,我们如何用已有的数据集去构建这么多的决策树呢?
首先我们要明白,决策树是不同的,那么训练决策树所需要的数据也不同。那么具体该如何选择呢?既然是随机森林,那么它肯定是随机的!!它的随机有两层含义:
样本随机使用的是Bagging算法(Bootstrap aggregating,引导聚集算法)又称之为装袋算法。算法的流程如下:
给定一个训练集大小为\(n\)的训练集\(D\),Bagging算法从中间随机的、有放回的选出\(m\)个大小为\(n'\)的子集\(D_i\)作为新的训练集。
ps:通过以上这种取样得到的集合\(D_i\)中间可能会有重复的元素(因为是有放回的抽取元素)
若样本有\(M\)个属性时,随机从这\(M\)个属性中选取出\(m\)个属性(无放回),满足条件\(m < M\)。
ps:在这种情况下,\(m\)个属性中是没有重复的属性的。
通过上面的样本随机和属性随机,我们就可以构建出很多棵不同的决策树了,然后组成一个森林,里面住着熊大和熊二,在一起快乐的生活。
优缺点的整理来自这里,基本上所有的文章都是这个说法,不同的在于文字的多少罢了!
优点
缺点
决策树的概念就暂时介绍到这里了,尽管内容有点多,但是还是挺好理解的,很类似于人类的思考方式。在下一篇的博客中,将使用scikit-learn工具包,基于决策树来对数据进行分类。决策树还有很多知识和算法,但是至少我们得掌握基本的概念。
标签:zoom 思想 关联 inf 集中 res 机器 度量 取值
原文地址:https://www.cnblogs.com/xiaohuiduan/p/12490064.html