标签:http width mamicode 就是 pac sort 高度 一个 cst
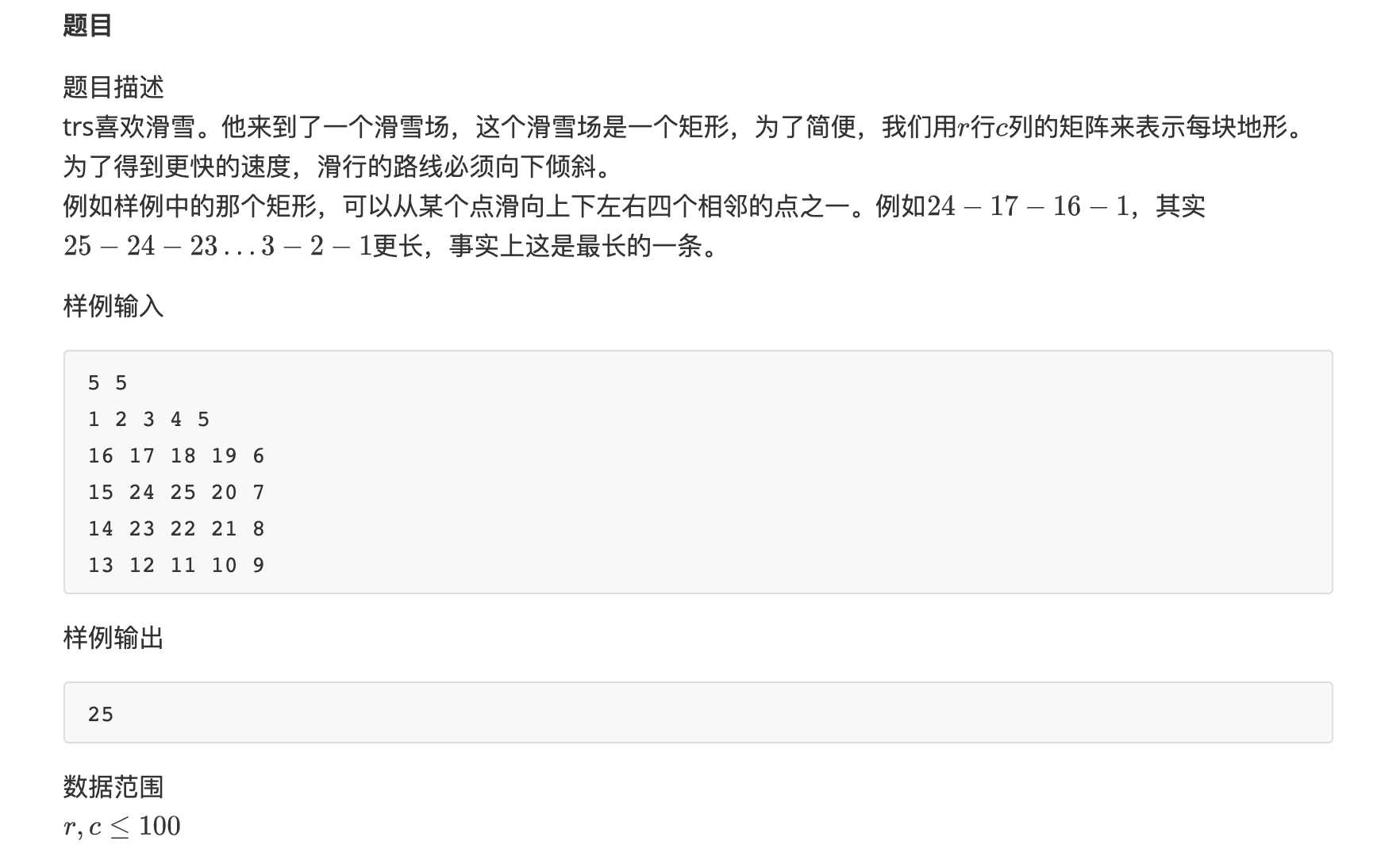
很容易想到用DP或记忆化搜索解决。
状态转移方程: dp[i][j] = MAX(dp[i][j] , 1 + dp(neighbor) ) 注意dp[i][j] 先要全部置1
由于记忆化搜索的做法没什么特别的,就是一个dfs+标记数组,就不多写了。
如何DP?这道题显然不能常规的线性DP,因为子问题并非线性排列的。
应该将每个点按照高度从小到大排序,然后才能转化成线性DP。
1 #include <cstdio> 2 #include <vector> 3 #include <algorithm> 4 #define MAX(a,b) (a>b?a:b) 5 #define Maxsize 100+1 6 using namespace std; 7 int arr[Maxsize][Maxsize]; 8 int dp[Maxsize][Maxsize]; 9 struct node{ 10 int val; 11 int x; 12 int y; 13 node(int a,int b,int c){ 14 val = a; x = b; y = c; 15 } 16 }; 17 vector<node> vec; 18 bool comp(const node&a,const node&b){ 19 return a.val < b.val; 20 } 21 int main(){ 22 int n,m; 23 scanf("%d %d",&n,&m); 24 for (int i = 1; i <= n; i++) { 25 for (int j = 1; j <= m; j++) { 26 scanf("%d",&arr[i][j]); 27 vec.push_back(node(arr[i][j],i,j)); 28 } 29 } 30 sort(vec.begin(),vec.end(),comp); 31 for (auto it = vec.begin();it != vec.end(); it++) { 32 dp[it->x][it->y] = 1; 33 if(it->x - 1 >= 1 && arr[it->x][it->y] > arr[it->x-1][it->y]){ // 上 34 dp[it->x][it->y] = MAX(dp[it->x][it->y],1 + dp[it->x-1][it->y]); 35 } 36 if (it->x + 1 <= n && arr[it->x][it->y] > arr[it->x+1][it->y]) { // 下 37 dp[it->x][it->y] = MAX(dp[it->x][it->y],1 + dp[it->x+1][it->y]); 38 } 39 if(it->y - 1 >= 1 && arr[it->x][it->y] > arr[it->x][it->y-1]) { // 左 40 dp[it->x][it->y] = MAX(dp[it->x][it->y],1 + dp[it->x][it->y-1]); 41 } 42 if(it->y + 1 <= m && arr[it->x][it->y] > arr[it->x][it->y+1]) { // 右 43 dp[it->x][it->y] = MAX(dp[it->x][it->y],1 + dp[it->x][it->y+1]); 44 } 45 } 46 int find_max = 0; 47 int ans = 0; 48 for (int i = 1; i <= n; i++) { 49 for (int j = 1; j <= n; j++) { 50 if (find_max < dp[i][j]) { 51 find_max = dp[i][j]; 52 ans = arr[i][j]; 53 } 54 } 55 } 56 printf("%d",ans); 57 return 0; 58 }
标签:http width mamicode 就是 pac sort 高度 一个 cst
原文地址:https://www.cnblogs.com/popodynasty/p/12490792.html