标签:基本 完全 border nbsp top http width 开始 bsp
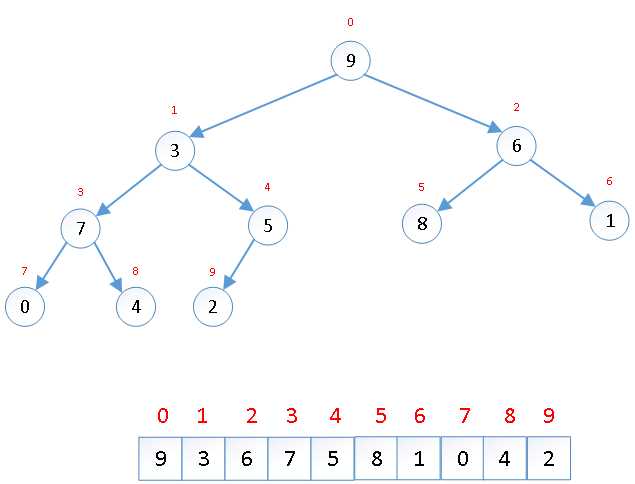
堆是一种特殊的完全二叉树,使用数组存储二叉树时,若某个非叶子节点存储在下标为i的位置,其左右孩子节点分别存储在下标为2i+1和2i+2的位置。
堆可以分为大顶堆和小顶堆,对大顶堆来说,任意非叶子节点不小于其左右孩子节点,对于小顶堆来说,任意非叶子节点不大于其左右孩子节点。若使用数组存储大顶堆,则满足:arr[i] >= arr[2i+1] && arr[i] >=arr[2i+2](i为非叶子节点的在数组中的下标)
基本思想:
1、从最后一个非叶子节点开始,逐一比较非叶子节点和其左右孩子节点
2、根据比较结果交换节点
3、因为交换可能导致孩子节点不再满足大顶堆的性质,所以需要对孩子节点进行调整。
例子:
|
初始 |
|
从最后一个非叶子结点开始,分别比较非叶结点和其左右孩子节点的大小。 无需调整 |
|
无需调整 |
|
无需调整 |
|
需要交换元素 |
|
无需调整 |
|
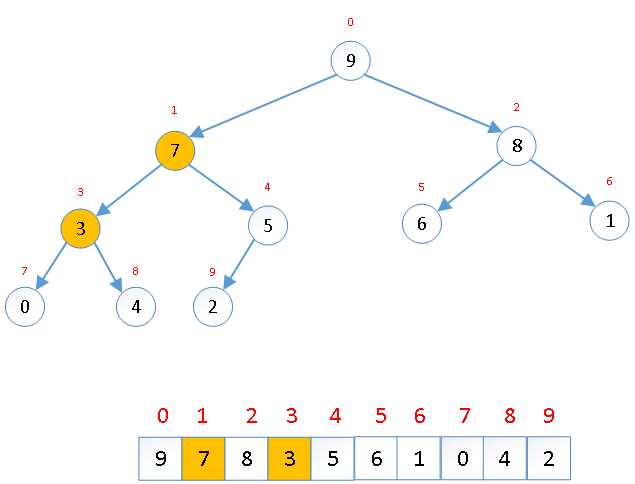
交换元素位置 |
 |
|
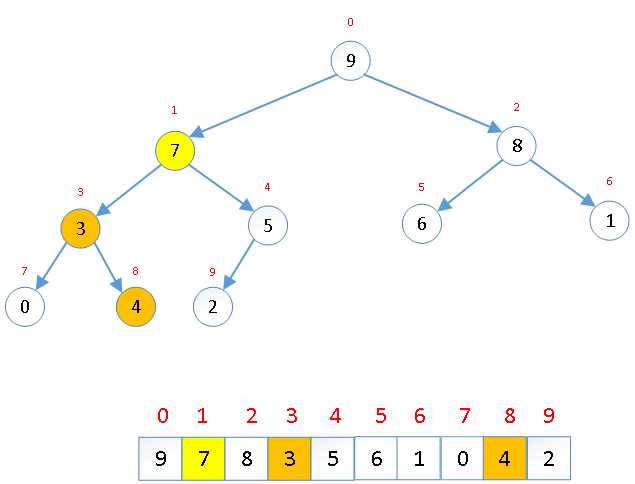
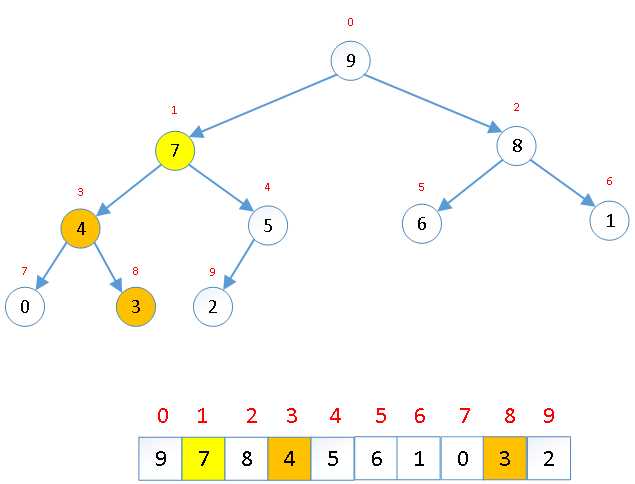
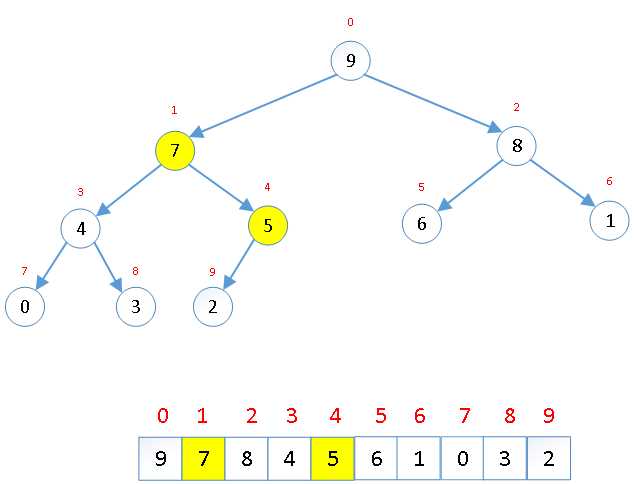
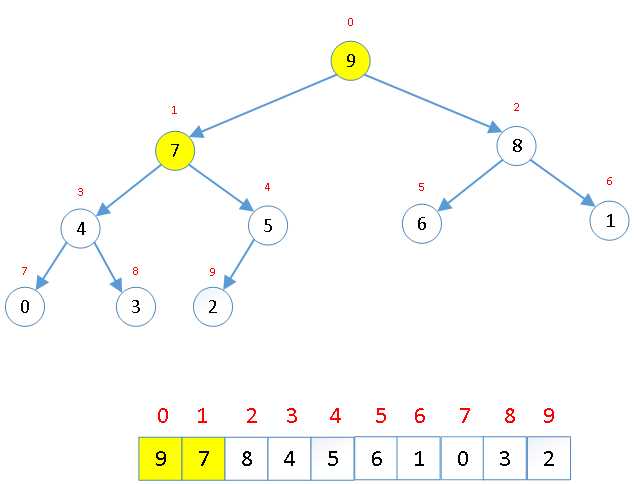
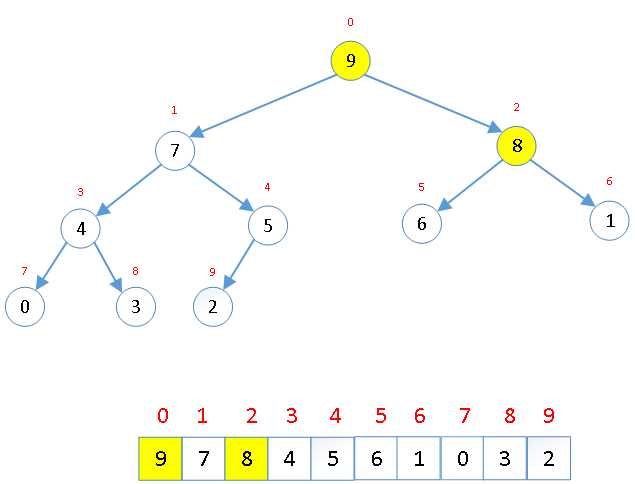
交换后可能造成被交换的孩子节点不满足堆的性质,因此每次交换后需要重新对交换的孩子节点进行调整。 |
 |
 |
|
 |
 |
|
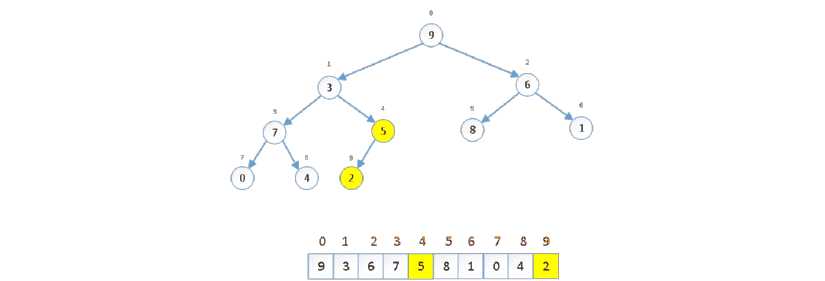
大顶堆建立完成 |
标签:基本 完全 border nbsp top http width 开始 bsp
原文地址:https://www.cnblogs.com/KenBaiCaiDeMiao/p/12492445.html