xor的最低位

标签：反向   dfs   完美   结果   src   void   ||   com   题目   

题目：

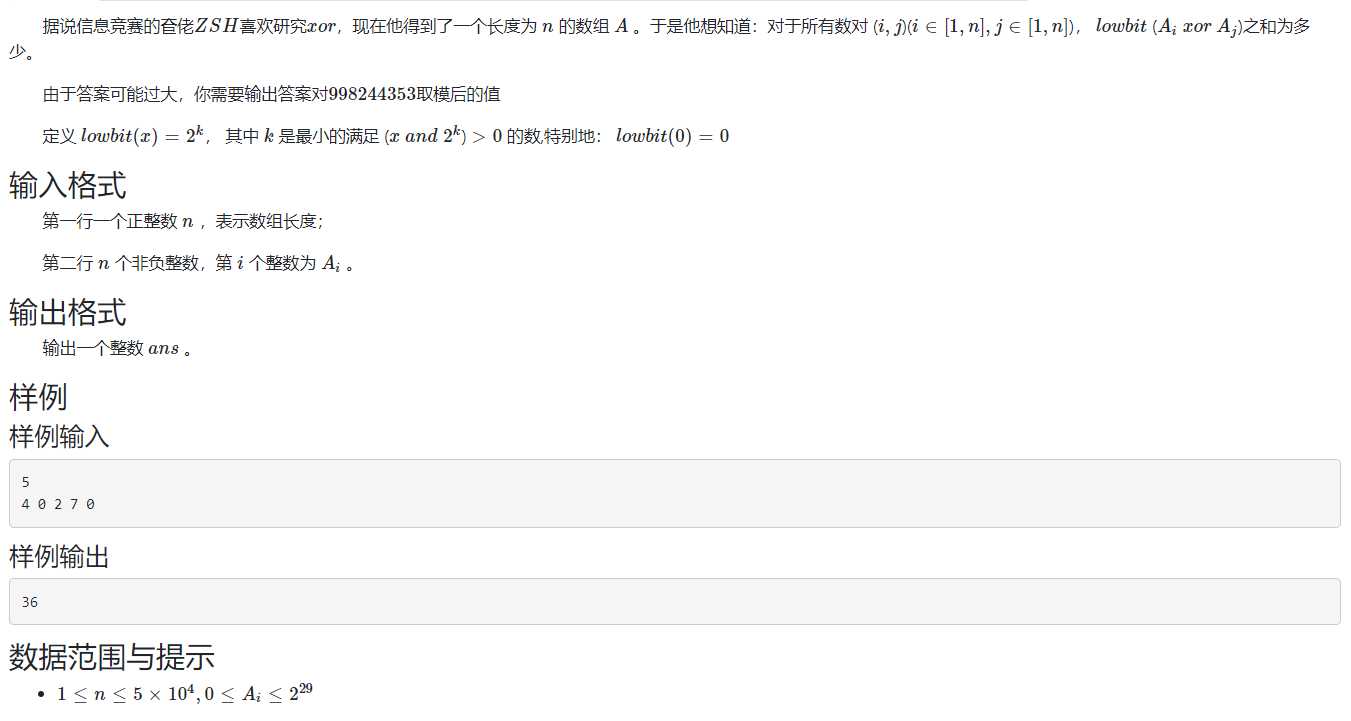
刚拿到这道题，我一开始就想到了01Trie树（解决\(xor\)的利器）

但是我上了一个模版就不会做了啊啊啊……

所以打了一个暴力，结果：\(0\space pts\)

话不多说，聊正解

正如上文所说，这题用01Trie树

那怎么做呢？

对答案有贡献的，就是两个数第一个不一样的地方。那这样子，把数都转化成二进制，然后建个字典树。（注意：反向建树，因为有\(lowbit\)计算。）经过的时候标记一下，就可以知道每个点有几个数经过。然后统计答案，就是分歧有几个，所以枚举父节点，它左右乘起来就是种类数。然后值是\(2^{dep}\)，\(dep\)是深度。简单来说，就是分歧那个地方，对应到二进制数里的大小。合起来就完成了。——信息老师指点语录

没听明白？那我用更好的语言再说一次

举个例子：

有两个数\(4\)和\(6\)，他们的二进制分别为：\((100)_2\)和\((110)_2\)

他们\(xor\)之后为\(2\)，所以\(lowbit\)值为2

此时发现：若用01Trie树来储存后缀，则一个节点所能贡献的值为左子树经过的数的个数\(\times\)右子树经过的数的个数\(\times\)这个点二进制下的数值（因为这里是分叉点，\(xor\)为\(0\)的到此结束，开始统计）

所以来一下dfs即可

warning：Trie树极易出现错误，请小心打、调；随时注意取模；模数不是一般的\(10^9+7\)这种

代码：

#include<bits/stdc++.h>
namespace my_std {
    using namespace std;
#define LL long long
    inline LL read() {
        char c=getchar();
        LL sum=0;
        while(c<'0'||c>'9') {
            c=getchar();
        }
        while(c>='0'&&c<='9') {
            sum=(sum<<3)-'0'+(sum<<1)+c,c=getchar();
        }
        return sum;
    }
    inline void write(LL x) {
        if(x>9) {
            write(x/10);
        }
        putchar(x%10+'0');
    }
    const LL d[4][2]= {
        {1,0},{0,1},{-1,0},{0,-1}
    },mod=998244353,N=1e5+5;
}
using namespace my_std;
struct Node {
    LL l,r,cnt;
} trie[N<<4]= {0};
LL tot=0,sum=0;
void build(LL x,LL now,LL time) {
    trie[now].cnt++;
    if(time==29) {
        return ;
    }
    if(x%2) {
        if(!trie[now].r) {
            trie[now].r=++tot;
        }
        build(x>>1,trie[now].r,time+1);
    } else {
        if(!trie[now].l) {
            trie[now].l=++tot;
        }
        build(x>>1,trie[now].l,time+1);
    }
}
void dfs(LL x,LL fsum,LL su) {
    sum%=mod;
    sum+=trie[x].cnt%mod*(fsum-trie[x].cnt)*su%mod;
    sum%=mod;
    if(trie[x].l) {
        dfs(trie[x].l,trie[x].cnt,su*2%mod);
    }
    if(trie[x].r) {
        dfs(trie[x].r,trie[x].cnt,su*2%mod);
    }
}
int main() {
    LL n=read();
    for(LL i=1,x; i<=n; i++) {
        x=read();
        build(x,0,0);
    }
    if(trie[0].l) {
        dfs(trie[0].l,n,1);
    }
    if(trie[0].r) {
        dfs(trie[0].r,n,1);
    }
    write(sum);
    return 0;
}

完美撒花~

后记：ZSH真的是大巨佬！！！

xor的最低位

标签：反向   dfs   完美   结果   src   void   ||   com   题目   

原文地址：https://www.cnblogs.com/Sam2007/p/12494488.html