标签:标记 最大 clu pen 包含 width double end max
http://codeforces.com/contest/1325/problem/C

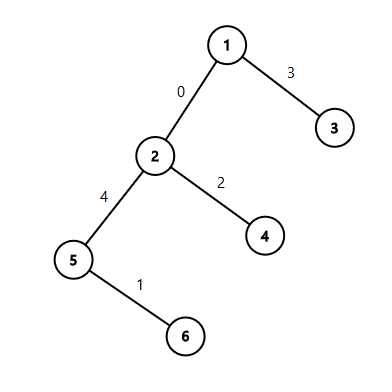
一棵树、n个点、n-1条边,构造边的值0 ~ n-2,使得对所有u,v来说,MEX(u,v)的最大值最小。(MEX(u,v)是指从u到v的简单路径中,所不包含的最小值)。
事实上,无论如何标记边,都会有一条路径穿过标记为0的边和标记为1的边,因此始终存在一条MEX为2或更多的路径。
如果任何节点的阶数为3或更高,则可以将标签0、1和2分布到与此节点关联的边,并任意分布其余标签。
否则,这棵树就是一根斜树,此时你如何标记边缘并不重要,因为无论如何都会有一条带有MEX为n-1的路径。
只要有一个点度数大于2,那么将其中的三个出边分别连0、1、2就可以了,剩下的随便连。
因为这样的话,mex一定是不大于2的,不可能有一个路径同时经过标记为0、1、2的这三条边。
1 #include <bits/stdc++.h> 2 const int INF=0x3f3f3f3f; 3 typedef long long LL; 4 const double eps =1e-8; 5 const int mod=1e9+7; 6 const int maxn=1e5+10; 7 using namespace std; 8 9 vector<int> vt[maxn]; 10 int ans[maxn]; 11 12 int main() 13 { 14 #ifdef DEBUG 15 freopen("sample.txt","r",stdin); 16 #endif 17 18 int n; 19 scanf("%d",&n); 20 for(int i=1;i<n;i++) 21 { 22 int u,v; 23 scanf("%d %d",&u,&v); 24 vt[u].push_back(i); 25 vt[v].push_back(i); 26 ans[i]=-1; 27 } 28 int cnt=0; 29 for(int i=1;i<=n;i++) 30 { 31 if(vt[i].size() > 2) 32 { 33 for(int id : vt[i]) 34 if(ans[id]==-1) ans[id]=cnt++; 35 } 36 } 37 for(int i=1;i<n;i++) 38 if(ans[i]==-1) ans[i]=cnt++; 39 for(int i=1;i<n;i++) 40 printf("%d\n",ans[i]); 41 42 return 0; 43 }
标程:
1 #include <bits/stdc++.h> 2 using namespace std; 3 vector<int> v[100005]; 4 int ans[100005]; 5 int main() 6 { 7 int n; 8 scanf("%d",&n); 9 for (int i=1;i<n;i++) 10 { 11 int a,b; 12 scanf("%d%d",&a,&b); 13 v[a].push_back(i); 14 v[b].push_back(i); 15 ans[i]=-1; 16 } 17 pair<int,int> mx(0,0); 18 for (int i=1;i<=n;i++) 19 mx=max(mx,make_pair((int)v[i].size(),i)); 20 int cur=0; 21 for (int i:v[mx.second]) 22 ans[i]=cur++; 23 for (int i=1;i<n;i++) 24 { 25 if (ans[i]==-1) 26 ans[i]=cur++; 27 printf("%d\n",ans[i]); 28 } 29 }
-
CodeForces 1325C Ehab and Path-etic MEXs(思维)
标签:标记 最大 clu pen 包含 width double end max
原文地址:https://www.cnblogs.com/jiamian/p/12495788.html