随机森林和Adaboost的对比

标签：regress   筛选   关注   The   计算   创建   apt   方差   dict   

随机森林算法：

随机森林利用随机的方式将许多决策树组合成一个森林，每个决策树在分类的时候决定测试样本的最终类别

在Bagging策略的基础上进行修改后的一种算法

从样本集中用Bootstrap采样选出n个样本；

从所有属性中随机选择K个属性，选择出最佳分割属性作为节点创建决策树；

重复以上两步m次，即建立m棵决策树；

这m个决策树形成随机森林，通过投票表决结果决定数据属于那一类

RF算法在实际应用中具有比较好的特性，应用也比较广泛，主要应用在：分类、

回归、特征转换、异常点检测等。常见的RF变种算法如下：

Extra Tree

Totally Random Trees Embedding(TRTE)

Isolation Forest

#Import Lib
From sklearn.ensemble import RandomForestClassifier
#use RandomForestRegressor for regression problem
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create Random Forest object
model= RandomForestClassifier(n_estimators=1000)
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)

RF的主要优点：

1. 训练可以并行化，对于大规模样本的训练具有速度的优势；

2. 由于进行随机选择决策树划分特征列表，这样在样本维度比较高的时候，仍然具有比较高的训练性能；

3. 给以给出各个特征的重要性列表；

4. 由于存在随机抽样，训练出来的模型方差小，泛化能力强；

5. RF实现简单；

6. 对于部分特征的缺失不敏感。

RF的主要缺点：

1. 在某些噪音比较大的特征上，RF模型容易陷入过拟合；

2. 取值比较多的划分特征对RF的决策会产生更大的影响，从而有可能影响模型的效果

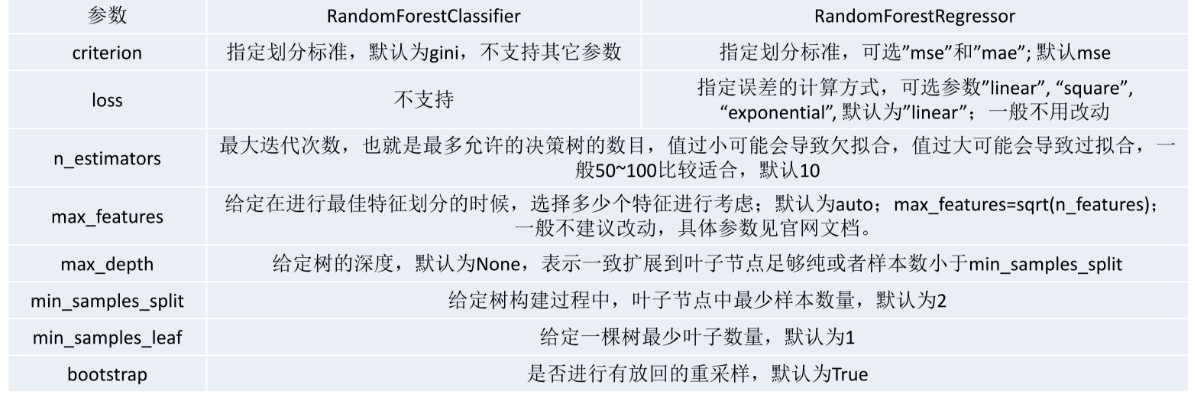
==随机森林参数==

Adaboost算法

基于数据集多重抽样的分类器

? Adaboost 是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器（弱分类器），然后把这些弱分类器集合起来，构成一个更强的最终分类器（强分类器）

? Adaboost 算法本身是通过改变数据分布来实现的，它根据每次训练集中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据送给下层分类器进行训练，最后将每次得到的分类器融合起来，作为最后的决策分类器

• Adaptive Boosting是一种迭代算法。每轮迭代中会在新训练集上产生一个新的学习器，然后使用该学习器对所有样本进行预测，以评估每个样本的重要性 (Informative)。换句话来讲就是，算法会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本，如果某个样本点被预测的越正确，则将其权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大，也就是说越难区分的样本在训练过程中会变得越重要；

• 整个迭代过程直到错误率足够小或者达到一定的迭代次数为止

• Adaboost算法将基分类器的线性组合作为强分类器，同时给分类误差率较小的基分类器以更大的权值，给分类误差率较大的基分类器以小的权重值。

 Adaboost 算法核心思想

“关注”被错分的样本，“器重”性能好的弱分类器实现：

• 不同的训练集：调整样本权重

• “关注”：增加错分样本权重

• “器重”：好的分类器权重大

• 样本权重间接影响分类器权重：样本权重-分类器-性能（错误率）-分类器的权重

 adaboost算法构造过程

1. 假设训练数据集?

2. 初始化训练数据权重分布

3. 使用具有权值分布Dm的训练数据集学习，得到基本分类器

4. 计算Gm(x)在训练集上的分类误差

5. 计算Gm(x)模型的权重系数αm

6. 权重训练数据集的权值分布

7. 权重归一化

8. 构建基本分类器的线性组合

9. adaboost参数

    adaboost优缺点

   Adaboost 算法优缺点

   优点：

   1）Adaboost 是一种有很高精度的分类器

   2）可以使用各种方法构建子分类器，Adaboost 算法提供的是框架

   3）当使用简单分类器时，计算出的结果是可以理解的，而弱分类器构造极其简单

   4）简单，不用做特征筛选

   AdaBoost的优点如下：

   • 可以处理连续值和离散值；

   • 解释强，结构简单。

   AdaBoost的缺点如下：

   • 对异常样本敏感，异常样本可能会在迭代过程中获得较高的权重值，最终影响模型效果。

   Adaboost 算法应用场景

   1）用于二分类应用场景

   2）用于做分类任务的 baseline--无脑化，简单，不用调分类器

   3）Boosting 框架用于对 badcase 的修正--只需要增加新的分类器，不需要变动原有分类器

    

    

    

随机森林和Adaboost的对比

标签：regress   筛选   关注   The   计算   创建   apt   方差   dict   

原文地址：https://www.cnblogs.com/pika-1/p/12500074.html