加密学详细介绍

标签：流程   proc   非对称加密   加密和解密   详细介绍   避免   之间   des   散列   

? 密码锁：是对里面贵重东西进行加密
? 钥匙：对加密的锁进行解密

? 计算机只能识别0和1两个数字 将现在世界中的东西映射为比特序列的操作称为编码
m -> 01101101
i -> 01101001
d -> 01100100
n -> 01101110
i -> 01101001
g -> 01100111
h -> 01101000
t -> 01110100
? 异或运算
异或运算的举例
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0
结论：可以根据B和C推到出A
0 1 0 0 1 1 0 0 A
1 0 1 0 1 0 1 0 B
1 1 1 0 0 1 1 0 C
? 加密和解密的初始模型

对称加密

? 对称加密 又称为共享密钥加密，它使用同一个密钥对数据进行加密和解密
? 适合于加密大数据
? 算法：DES（56bit） 3DES（168bit） AES（比较多）

工作原理

? 发送方:
明文数据 ------------对称算法（DES-56bit）-----------得到密文数据
得到56bit的密钥
? 接收方：
提前获知56bit密钥-------解密密文数据--------明文数据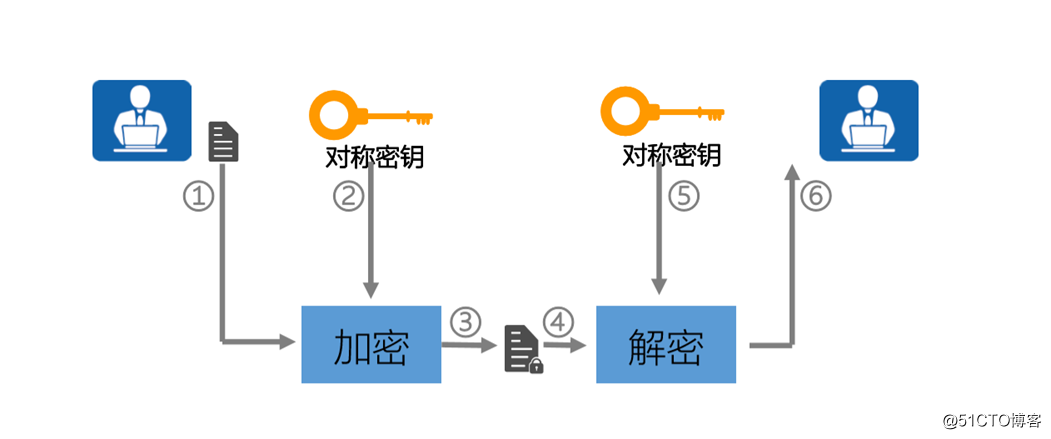

优点

? 速度快 适合对大数据进行加密
? 安全
? 紧凑 加密1G的数据 加密出来之后 密文数据大概1G左右

缺点

? 明文传输共享密钥，容易出现中途劫持和窃听的问题 很难保证密钥不被泄露
? 密钥数量是以参与者数量平方的速度增长（指数增长）
? 因为数量过多，所以管理和存储会有很大问题
? 不支持数字签名和不可否认性

非对称加密

? 非对称加密 会产生一个密钥对 公钥和私钥 本质就是公钥加密 私钥解密
? 加解密使用两个不同的密钥，公钥则由同一系统的人公用，用来检验信息及其发送者的真实性和身份 私钥用来保护数据
? 算法：RSA（用的比较多） DSS ECC DH（只能ipsec里面用 DH算法没有公钥和私钥）
? 适合加密一些小数据

工作原理

? 发送方（加密过程）
明文数据（假如是一个PDF文件的话）-------------对端的公钥加密------------密文数据（PDF）

? 接收方（解密过程）
密文数据(PDF)----------------------------------自己的私钥解密-----------得到明文数据（PDF）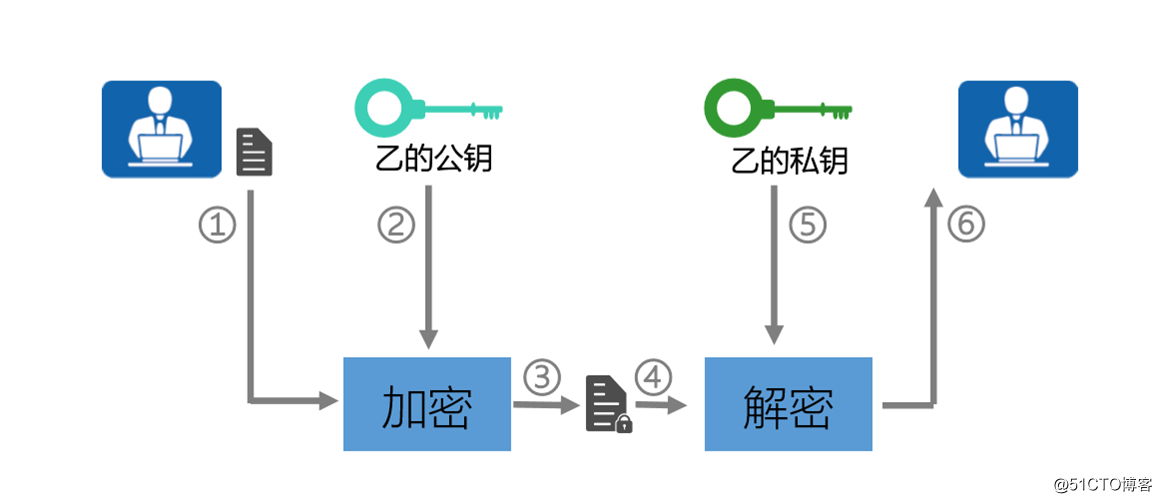

RSA算法实现非对称算法的过程

有专门的PGP软件可以实现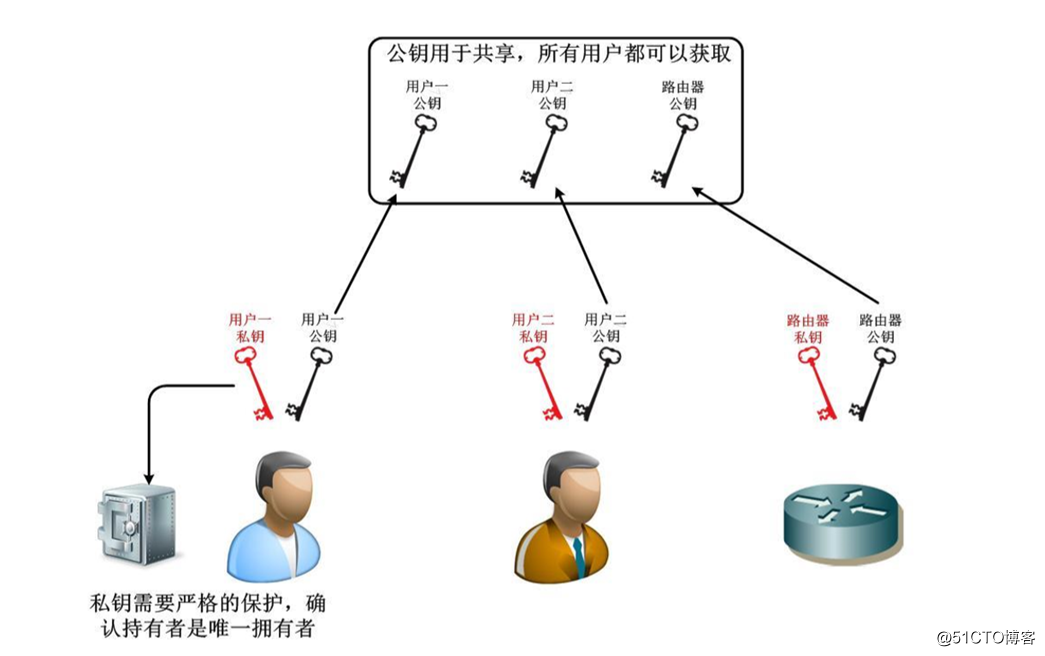

RSA的加密过程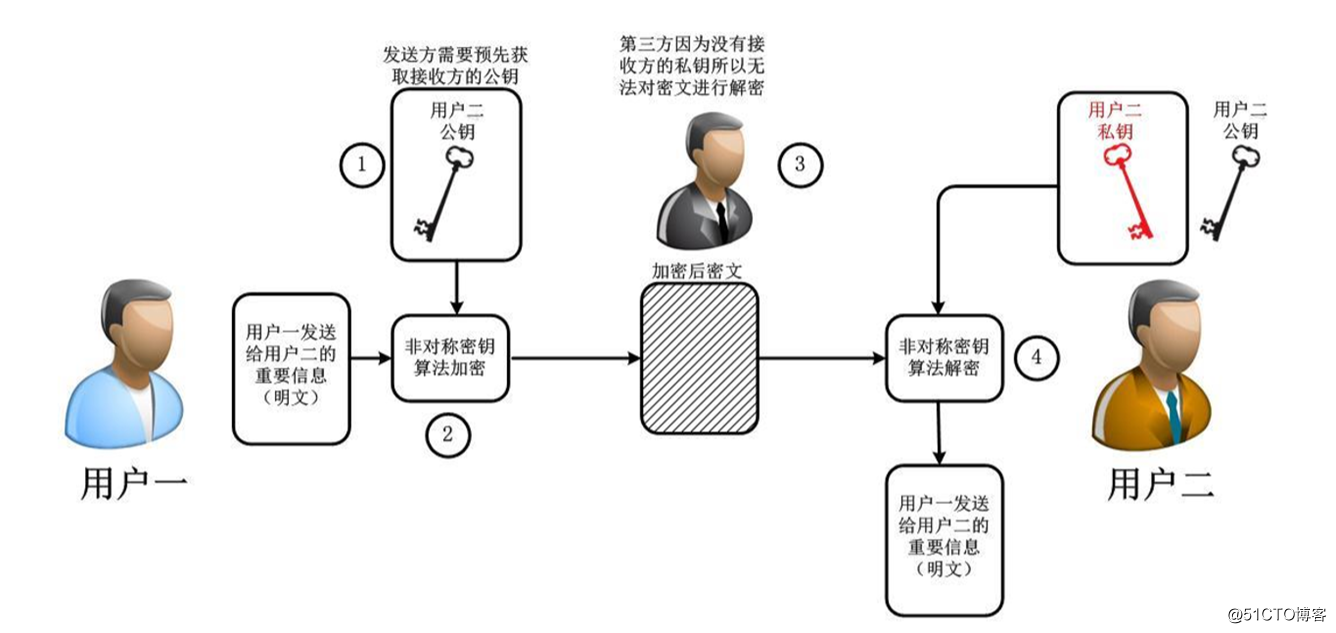

缺点

1. 非常非常非常长
   100M的数据通常加密后就成了200M 所以非对称适合加密一些小数据
2. 非常非常非常慢
   对称加密是非对称的速度1千倍
3. 无法抵御中间人***

   优点

   ? 安全
   ? 因为不必发送密钥给接受者，所以非对称加密不必担心密钥被中途截获的问题
   ? 密钥数目和参与者的数目一样
   ? 不需要事先在各参与者之间建立关系以交换密钥
   ? 技术支持数字签名和不可否认性

   中间人***

   上述流程会有一个问题：Client端如何保证接受到的公钥就是目标Server端的？，如果一个***者中途拦截Client的登录请求，向其发送自己的公钥，Client端用***者的公钥进行数据加密。***者接收到加密信息后再用自己的私钥进行解密，不就窃取了Client的登录信息了吗？这就是所谓的中间人***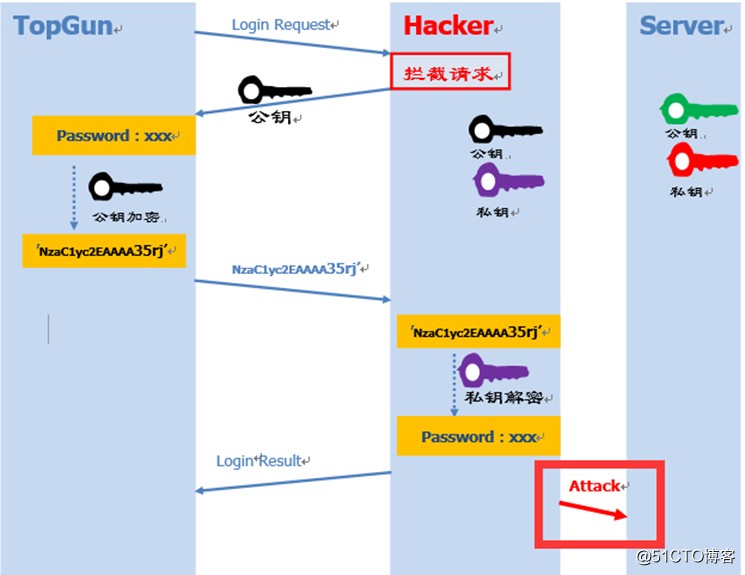
   

   对称加密和非对称加密区别

   

   数字信封

   ? 本质就是对称算法和非对称算法结合
   ? 其中对称算法是为了加密大数据 一般用于加密数据流
   ? 其中非对称算法是为了传输对称算法所产生的密钥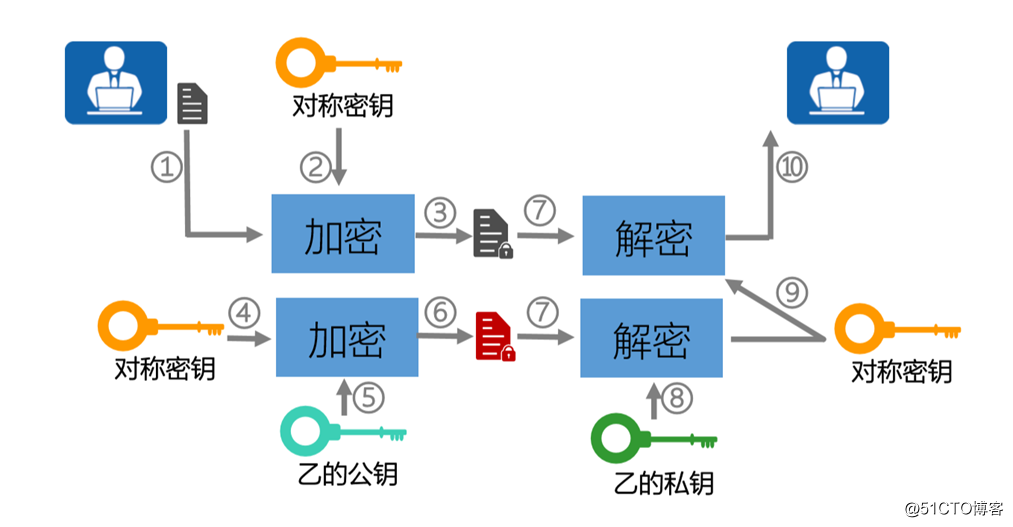
   

   工作原理

   发送方（加密过程）
   明文数据（大数据）----------对称算法加密-------------密文数据
   产生DES 56bit
   对端的公钥加密这个56bit的密钥 ------------得到就是密钥包

把密文数据和密钥包一起发给对端叫数字信封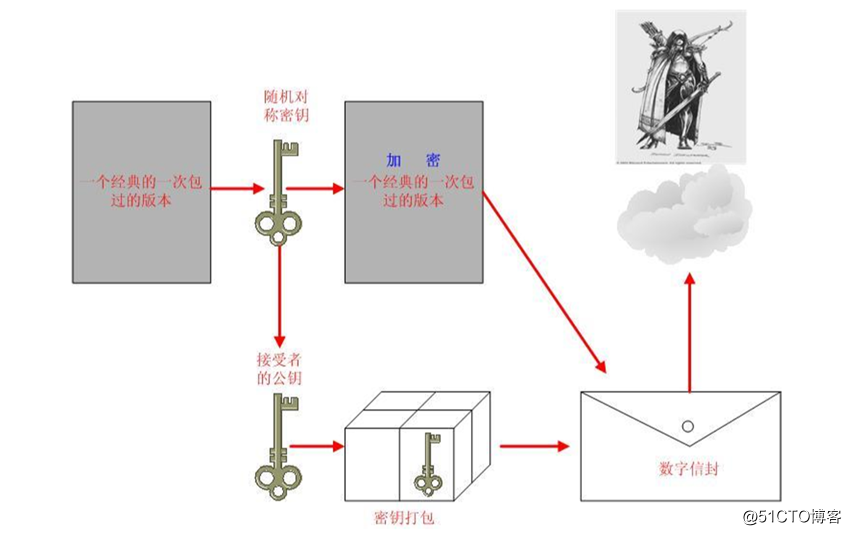

接收方（解密过程）
把数字信封里面的密文数据和密钥包 -------------------自己的私钥解密-----------得到DES 56bit对称算法的密钥-------把密文的数据用得到的DES 56bit密钥解密----------得到明文的数据（大数据）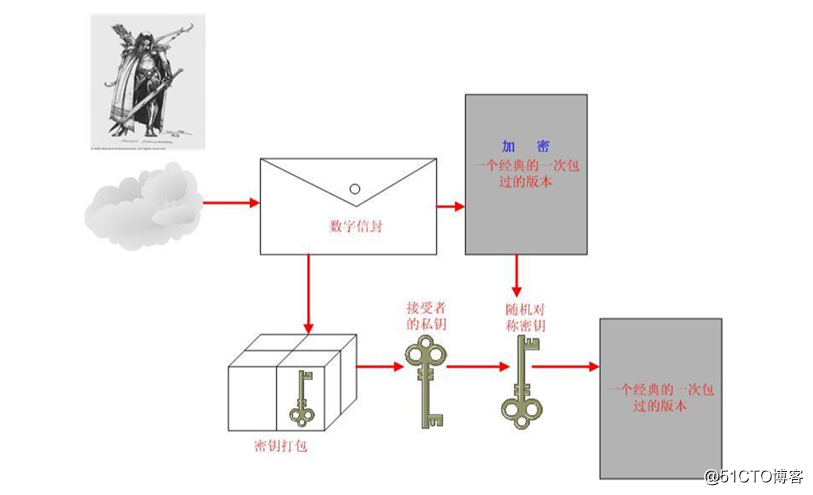

数字签名

? 为了验证数据的完整性
? 数字签名 实现数据的完整性采用私钥加密，公钥解密
? 实现算法：HASH函数（散列函数） MD5 SHA-1 SHA-2
指纹的工作示意图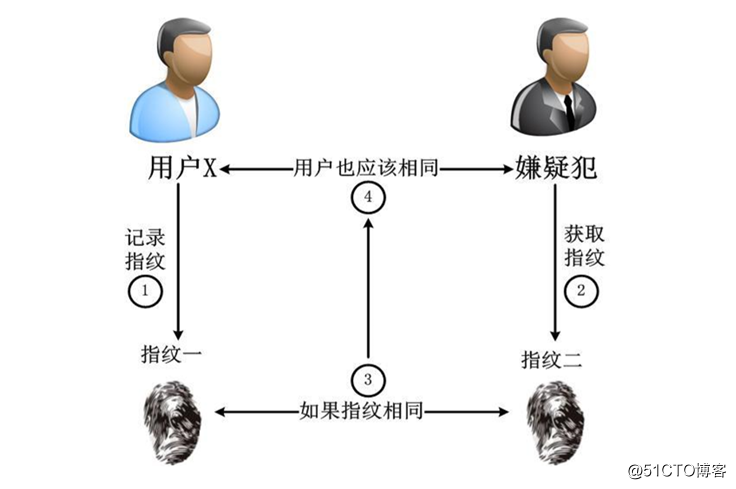

散列函数工作示意图
可以用MD5校验工具实验下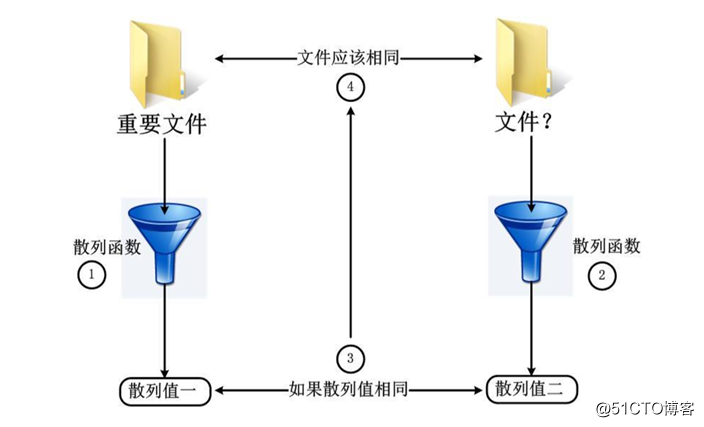

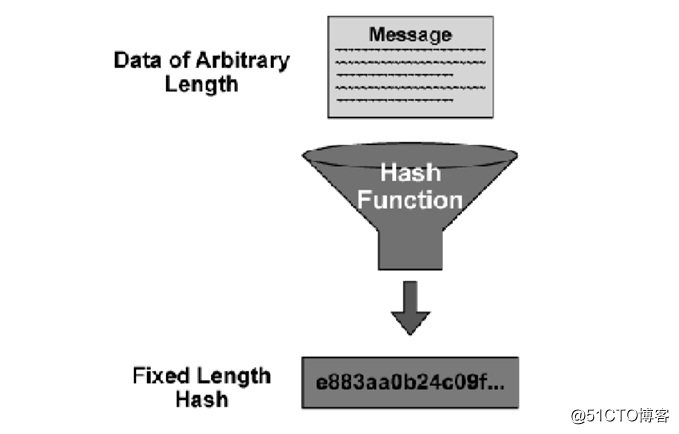
特点:

? 固定输出
? 雪崩效应
? 单向不可逆
? 冲突避免

工作原理：

签名过程：
明文数据-----------HSAH算法(MD5)-----------明文的HASH值1 ----------自己的私钥加密--------得到数字签名
把明文数据+数字签名一起发给对端

解签名过程：
对方的公钥-------解密数字签名----------得到HASH值1

明文数据---------使用相同的HASH算法(MD5)------得到HASH值2
如果HASH值1 与HASH值2相同，说明数据是完整的，没有被修改或者篡改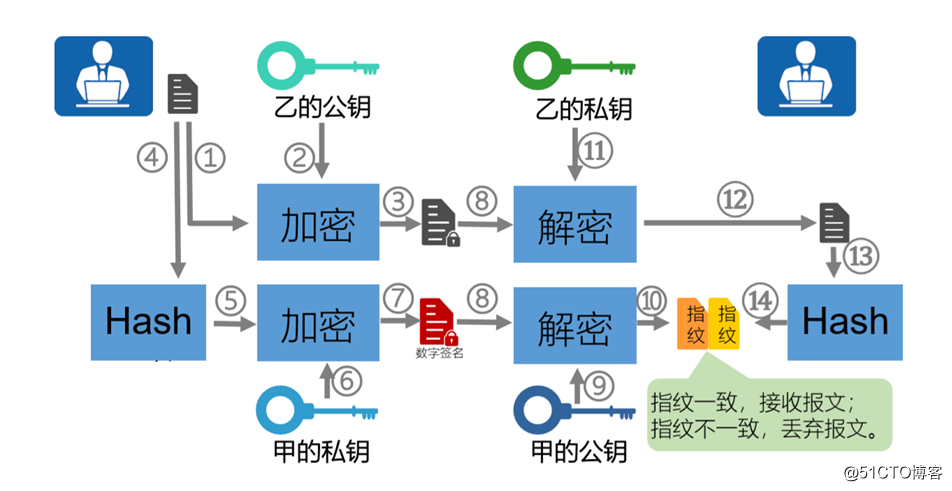

加密学详细介绍

标签：流程   proc   非对称加密   加密和解密   详细介绍   避免   之间   des   散列   

原文地址：https://blog.51cto.com/13817711/2478448