统计学习,或者说机器学习的方法主要由监督学习、无监督学习和强化学习组成(它们是并列的,都属于统计学习方法)。
1、假设数据独立同分布。(同数据源的不同样本之间相互独立)
2*、假设要学习的模型属于某个函数的集合,称为假设空间。(你确定了这个函数的样式,就是假设空间,但是函数里面的参数不确定,要学习。学习的是参数,比如把$y = 2x_1 + 3x_2$学成了$y = 3x_1+2x_2$,而不能学成$y = 3x_1^2+3x_2$)
3、应用某个评价准则,从假设空间中选一个最优模型,让模型对输入(训练数据或测试数据)具有最优预测。(构造一个损失函数,作为优化的判断依据)
4、使用一定的算法优化这个损失函数。
所以它的三要素是:模型(2)、策略(3)、算法(4)。
1、得到一个有限的训练数据集合。
2、确定包含所有可能的模型的假设空间,即学习模型的集合。
3、确定模型选择的准则,即学习的策略。
4、实现求解最优模型的算法,即学习的算法。
5、通过学习方法选择最优模型。
6、利用学习的最优模型对新数据进行预测或分析。
统计学习或机器学习一般包括监督学习、无监督学习、强化学习。有时还包括半监督学习、主动学习。
监督学习是指从标注数据中学习预测模型的问题。
标注数据表示输入到输出的关系,目标是让模型能通过输入预测输出,也就是学习输入到输出的映射的统计规律。
训练集由n个输入向量$x_i$和输出$y_i$的对组成:
$T = \{(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\}$
输入实例$x_i$用向量表示:
$x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)})^T$
监督学习的应用中,根据输入和输出的连续或是离散,训练模型的任务又取名为不同的名称:(注意!这是在监督学习中的分类)
1、回归问题:输入变量和输出变量都是连续变量。
2、分类问题:输出变量为有限的离散变量。(算上回归问题,就剩输入为有限离散,输出为连续变量这种情况没考虑,但是这个没有现实意义,所以没有。并且无限离散变量也没有现实意义。)
3、标注问题:输入与输出均为变量序列(向量)的预测问题是标注问题,实际上就是分类问题或是回归问题的推广。
监督学习假设输入$X$与输出$Y$遵循联合概率分布$P(X, Y)$。所以学习的过程就是拟合这个联合概率分布的过程。
因为联合概率分布的具体定义是未知的(所以要我们自己先假设一个假设空间,假设它符合某个分布,再通过机器学习来计算它的参数),并且我们无法获得样本全体,而只能通过有限的样本来估计它的分布,所以这就是机器学习的困难所在。
尽管我们假设输入输出服从某个分布,我们还是可以把模型分为概率模型和非概率模型(因为是监督学习,就是生成模型和判别模型),分别由条件概率分布$P(Y|X)$ 和决策函数$Y = f(X)$表示:
1、$P(Y|X)$ :假设一个联合分布分布$P(X, Y)$,使用回归问题任务来拟合联合概率分布$P(X, Y)$,预测$X = x$的输出分布时候就是通过这个联合概率分布计算条件分布$P(Y|X = x) = \frac{P(X = x, Y)}{\int P(X = x|Y = y)dy}$(这个学过概率论的人都知道)。 特殊地,对于$Y$是有限离散的情况,$P(Y|X = x)$就是几个离散值的概率分布,如:$P(Y=y_1,X=x)=0.2, P(Y=y_2,X=x)=0.3, P(Y=y_3,X=x)=0.5$。对于$Y$是连续的情况,$P(Y|X = x)$就是连续值$Y$的概率密度,如某个正态分布。
2、$Y = f(X)$:就没那么追求假设分布的过程了,它直接设一个函数,只求训练出函数的参数使得$f(X)$能够最大程度地接近真实$Y$,而预测时则直接代入$X$来计算$Y$的值。
书中关于监督学习的图:
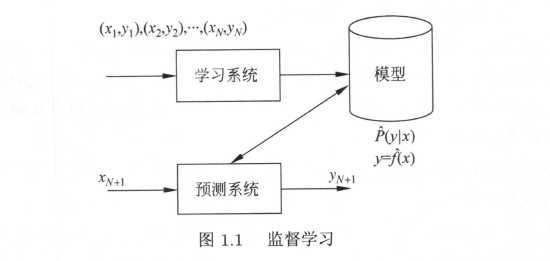
通过学习,模型表现为条件概率分布$\hat{P}(Y|X) $(由拟合出的联合分布除以$X$的边缘分布求出,边缘分布用联合分布对$Y$积分求出)或决策函数$Y = \hat{f}(X)$,上面加的符号表示拟合(非真实)的意思。预测时,通常分别用$y_{N+1} = \mathop{\arg\max}\limits_{y} \hat{P}(y|x_{N+1})$,$y_{N+1} = \hat{f}(x_{N+1})$给出相应的$y_{N+1}预测$。
无监督学习是指从无标注数据中学习预测模型的机器学习问题。本质是学习数据中的统计规律或潜在结构,可以实现对数据的聚类、降维或概率估计。
假设$\mathcal{X}$是输入空间,$\mathcal{Z}$是隐式结构空间。模型就可以表示为函数$z = g(x)$,条件概率分布$P(z|x)$或$P(x|z)$的形式,其中$x\in \mathcal{X}$为输入,$z\in \mathcal{Z}$为输出。
书中关于无监督学习的图:
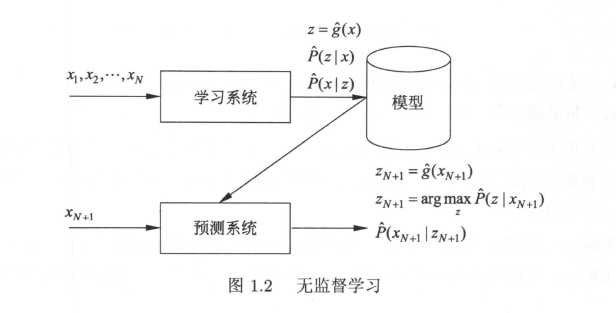
对于输入$x_{N+1}$,由上图的模型给出输出$z_{N+1}$,进行聚类、降维或统计概率。
强化学习是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。
半监督学习是指利用标注数据和未标注数据学习预测模型的机器学习问题。
主动学习是指机器不断主动给出实例让教师进行标注,然后利用标注数据学习预测模型的机器学习问题。
机器学习模型可以分为概率模型和非概率模型(确定性模型)。监督学习中又叫生成模型和判别模型(上面讲过),生成模型实际上学习到的是生成数据的机制。无监督模型中,概率模型就是用条件分布预测,非概率模型就是函数值直接预测(上面也讲过)。
决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯温合模型是概率模型。
感知机、支持向量机、k 近邻、AdaBoost 、k 均值、潜在语义分析,以及神经网络是非概率模型。
逻辑斯谛回归既可看作是概率模型,又可看作是非概率模型。
条件概率分布$P(y|x)$和函数$y = f(x)$可以相互转化:
具体地说,条件概率分布中取概率最大的$Y$就转变为了函数;
而函数值进行归一化后,就能获得条件概率分布,我的理解是:从预测$Y = f(X = x_i) = y_i$变成概率$P(Y=y_i|X=x_i) = 1, P(Y=y_{else}|X=x_i) = 0$。强制转换,好像没啥用,毕竟条件概率分布是通过联合概率分布获得的,这样直接转换没有任何意义。
所以,概率模型和非概率模型的区别不在于输入与输出之间的映射关系,而在于模型的内在结构。概率模型一定可以表示为联合概率分布的形式,其中的变量表示输入、输出、隐变量甚至参数。而针对非概率模型则不一定存在这样的联合概率分布,但是因为它直接预测输出的值,所以通常预测会更加准确一些。
概率模型的代表是概率图模型,概率图模型是联合概率分布由有向图或者无向图表示的概率模型,而联合概率分布可以根据图的结构分解为因子乘积的形式。(这个还要再学习一下)
非概率模型(函数)可以分为线性模型与非线性模型。如果函数$y = f(x) $或$z = g(x) $是线性函数,就是线性模型,否则就是非线性模型。
感知机、线性支持向量机、k 近邻、k 均值、潜在语义分析是线性模型。核函数支持向量机、AdaBoost 、神经网络是非线性模型。
参数化模型假设模型参数的维度固定,模型可以由有限维参数完全刻画;非参数化模型假设模型参数的维度不固定或者说无穷大,随着训练数据量的增加而不断增大。
感知机、朴素贝叶斯、逻辑斯谛回归、k 均值、高斯混合模型是参数化模型。决策树、支持向量机、AdaBoost 、k 近邻、潜在语义分析、概率潜在语义分析、潜在狄利克雷分配是非参数化模型。
统计学习根据算法,可以分为在线学习与批量学习。在线学习是指每次接受一个样本,进行预测,之后学习模型,并不断重复该操作的机器学习。批量学习一次接受所有数据,学习模型,之后进行预测。
有些实际应用的场景要求学习必须是在线的。比如:数据依次达到无法存储,系统需要及时做出处理。数据规模很大,不可能一次处理所有数据。数据的模式随时间动态变化,需要算法快速适应新的模式(不满足独立同分布假设)。
学习和预测在一个系统,每次接受一个输入$x_t$,用己有模型给出预测$\hat{f}(x_t)$ ,之后得到相应的反馈,即该输入对应的输出$y_t$;系统用损失函数计算两者的差异,更新模型;并不断重复以上操作。如图:
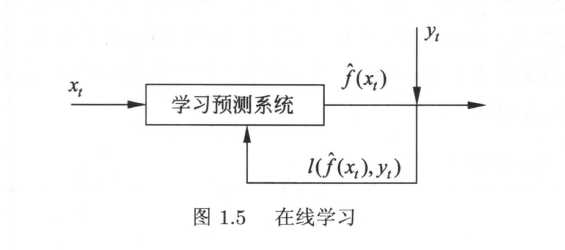
利用随机梯度下降的感知机学习算法就是在线学习算法。
这里的技巧不是三要素中的策略(损失函数),而是模型的选择。
****
****
了解先验概率、后验概率。贝叶斯学习,以及与最大似然的区别。
原文地址:https://www.cnblogs.com/qizhou/p/12229604.html