字典树-高效储存字符串

标签：复杂度   pac   于平   大数据   多路径   img   时间复杂度   标记   ++   

概述

本文介绍字典树的相关知识和实现。想知道ZMXQS与LXL的故事可以去你咕问一下“ZMXQS是谁”或“关于平衡树是什么梗”。

前置知识

C++风格和C风格的字符串。
树的概念与实现。

字典树是什么

字典树是一种用于保存大量字符串的高效数据结构。它的高效体现在时间和空间两个维度上。它可以实现O(m)时间复杂度的插入与删除（这里的m是字符串长度），以及在大数据情况下相对节省的空间。

原理

在介绍字典树的原理之前，我们先来看一看普通的字符串储存方法。

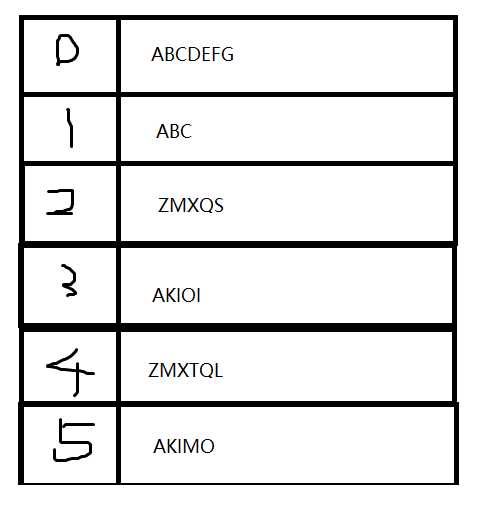
在这个典型的字符串数组中，每一个格子储存了一个字符串。每一次查找都需要O(n)地在整个数组中遍历比对，每一次比对又需要O(m)。如果使用链表来保存，则插入和删除可以做到O(m)，因为删除需要先找到，而插入也需要进行新开节点并赋值的操作。可以说，非常低效。

那么字典树使用什么样的方式来维护这些字符串等呢？首先我们上一张 小h 图，图中的字典树表示的就是上面的那些字符串。

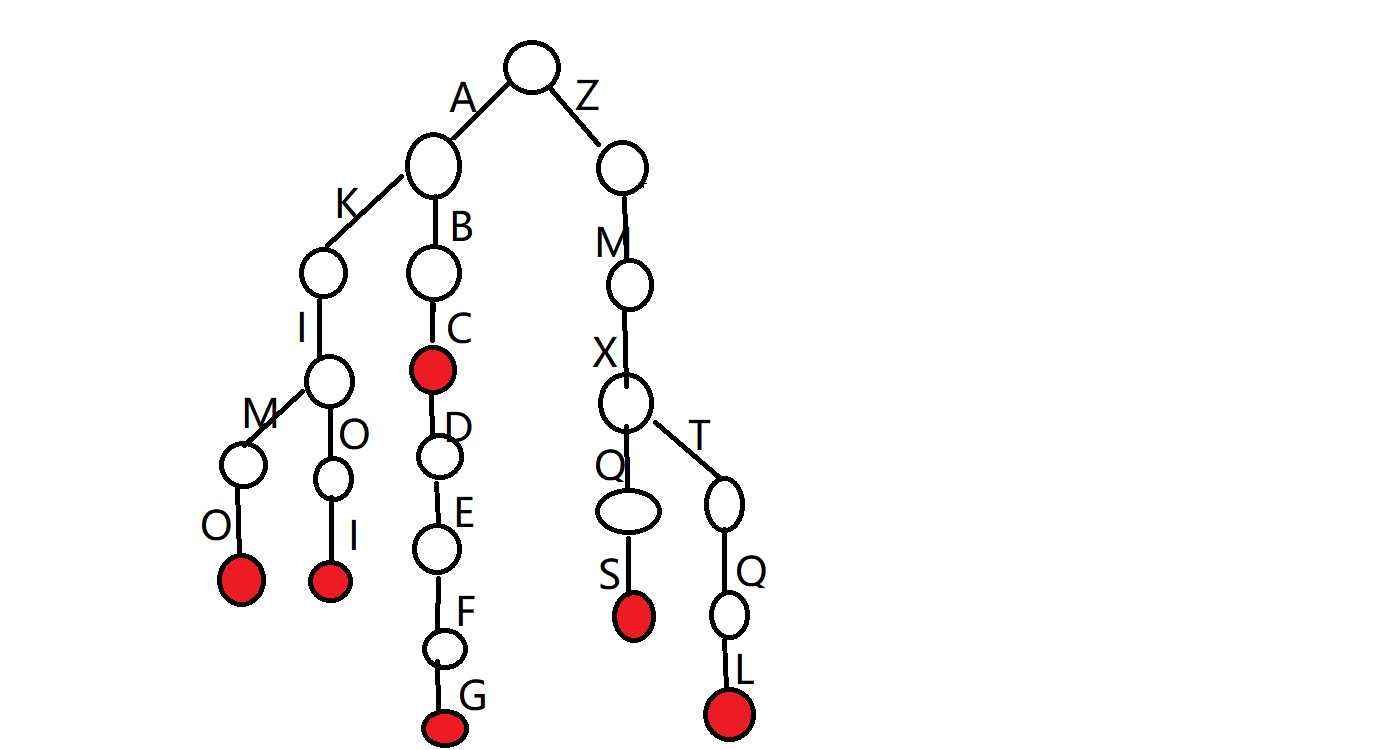
可以注意到，这张图中使用了树的结构来保存字符串。从根到每个节点的路径表达的就是一个字符串。这个时候旁边的ZMXQS拍案而起，你胡说八道！上面一张图里不是只有6个字符串么？这里有这么多路径，绝对不止6条，你一定是受了LXL的贿赂来毒害我们的！不急不急，为了过滤掉这些不合法的字符串，我们在节点上加一个标记，表示这个节点到根的路径是一个合法字符串（也可以理解成这个节点是否是一个字符串的末尾）。图中我们就是用染红来表示这个节点被标记了。

那么效率高在哪里呢？首先，在这棵树上，所有相同的前缀都只被储存了一次，比如ZMX，AK等，于是空间高效（当然这是在数据大、前缀多的情况下，因为为了储存指针，有不少冗余的空间）。第二，在这棵树上查找/插入/删除都只需要遍历一遍字符串，跟着指针走即可，时间也很高效。第三，没有第三（逃

其他应用

字典树还可以维护 集合中以某个串为前缀的字符串数量，具体只需要在每次插入字符串的时候把路径上所有节点的cnt都加一下，查询的时候输出cnt就可以了 好水的样子。这里我们认为 自己是自己的前缀。

实现

我们提供指针和数组两种实现，数组其实就是模拟指针。

指针

#include<bits/stdc++.h>


using namespace std;


struct Trie {
    bool isWordFinish;
    Trie * child[26];
    int preNum;

    Trie(void) {
        isWordFinish = false;
        for (int i = 0; i < 26; ++i) {
            child[26] = NULL;
        }
        preNum = 0;
    }
    ~Trie() {
        for (int i = 0; i < 26; ++i) {
            if (child[i] != NULL) {
                delete child[i];
            }
        }
    }
};


Trie * rt;


void insert(Trie * & rt, const char * str, int len);
void remove(Trie * & rt, const char * str, int len);
bool checkExist(Trie * rt, const char * str, int len);
int countPre(Trie * rt, const char * str, int len);


int main(void) {
    // TODO
    return 0;
}


void insert(Trie * & rt, const char * str, int len) {
    if (rt == NULL) {
        rt = new Trie;
    }
    if (len == 0) {
        ++rt->preNum;
        rt->isWordFinish = true;
    } else {
        ++rt->preNum;
        insert(rt->child[str[0] - 'a'], str + 1, len - 1);
    }
}

void remove(Trie * & rt, const char * str, int len) {
    if (rt == NULL) {
        throw "remove: Word not exist";
    }
    if (len == 0) {
        if (rt->isWordFinish) {
            rt->isWordFinish = false;
        } else {
            throw "remove: Word not exist";
        }
        --rt->preNum;
    } else {
        remove(rt->child[str[0] - 'a'], str + 1, len - 1);
        --rt->preNum;
    }
    if (rt->preNum == 0) {
        delete rt;
    }
}

bool checkExist(Trie * rt, const char * str, int len) {
    if (rt == NULL) {
        return false;
    }
    if (len == 0) {
        return rt->isWordFinish;
    }
    return checkExist(rt->child[str[0] - 'a'], str + 1, len - 1);
}

int countPre(Trie * rt, const char * str, int len) {
    if (rt == NULL) {
        throw "countPre: Word not exist";
    }
    if (len == 0) {
        if (rt->isWordFinish) {
            return rt->preNum;
        } else {
            throw "countPre: Word not exist";
        }
    }
    return countPre(rt->child[str[0] - 'a'], str + 1, len - 1);
}

数组代码咕咕咕了，待更新。

字典树-高效储存字符串

标签：复杂度   pac   于平   大数据   多路径   img   时间复杂度   标记   ++   

原文地址：https://www.cnblogs.com/KevinYao-Blog/p/12525318.html