LeetCode日常刷题

标签：poi   平衡   array   cte   bool   image   超过   区间   min   

[1] 125. 验证回文串【简单】

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

输入: "A man, a plan, a canal: Panama"
输出: true

示例 2:

输入: "race a car"
输出: false

class Solution:
    def isPalindrome(self, s: str) -> bool:
        # 回文串，即正读和反读一样的字符串
        # 去掉字符串中的空格和字符，那么字符串是对称的
        s = "".join(filter(str.isalnum,s)).lower()
        return s == s[::-1]

代码中的知识点：

filter()        # python语言中的过滤函数
str.isalnum     # 过滤函数满足的条件为，字母和数字
str.lower()     # 将字符串中的字符转为小写
str.upper()     # 将字符串中的字符转换为大写
chr()           # 将数字转为字符，其中大写字母的范围为65——90，小写字母为97——122，数字为48——57
ord()           # 将字符转为数字，与chr()相反
s == s[::-1]    # 将字符串倒转

对于上述问题，首先想到的是字符的replace()函数，但是当字符串中的特殊字符太多，如果仅仅使用字符串的replace()函数难以实现。我们想到了 正则表达式。

re.compile()    # 构建要匹配的模式，对于要匹配的模式，一种是找出字符串中的字母和数字；另一种是找出特殊字符作为分隔符
re.split()      # 通过特殊字符串对字符串进行分割后合并，实验发现，可能结果太多了
re.findall()    # 寻找字母和数字,匹配字符为"\w"，匹配的是单词字符[A-Za-z0-9_]

生成代码：

class Solution:
    def isPalindrome(self, s: str) -> bool:
        # 回文串，即正读和反读一样的字符串
        # 去掉字符串中的空格和字符，那么字符串是对称的
        import re
        s = s.lower()
        p = re.compile("\w")
        s = "".join(p.findall(s))
        print(s)
        return s == s[::-1]

[2] 859. 亲密字符串【简单】

给定两个由小写字母构成的字符串 A 和 B ，只要我们可以通过交换 A 中的两个字母得到与 B 相等的结果，就返回 true ；否则返回 false 。

示例 1：

输入： A = "ab", B = "ba"
输出： true

示例 2：

输入： A = "ab", B = "ab"
输出： false
字符串相同，且重复的字符串小于2，返回False

示例 3:

输入： A = "aa", B = "aa"
输出： true
字符串相同，且存在2个及两个以上的重复的字符串，返回True

示例 4：

输入： A = "aaaaaaabc", B = "aaaaaaacb"
输出： true

示例 5：

输入： A = "", B = "aa"
输出： false
长度不同，返回False

提示：

1. 0 <= A.length <= 20000
2. 0 <= B.length <= 20000
3. A 和 B 仅由小写字母构成

官方题解, 其实情况没有那么多, 就三种情况:

1. 字符串长度不相等, 直接返回false
2. 字符串相等的时候, 只要有重复的元素就返回true
3. A, B字符串有不相等的两个地方, 需要查看它们交换后是否相等即可.

class Solution:
    def buddyStrings(self, A: str, B: str) -> bool:
        if len(A) != len(B):
            return False
        if A == B and len(set(A)) < len(A):
            return True
        resArr = []
        for i in range(len(A)):
            if A[i] != B[i]:
                resArr.append(A[i]+B[i])
        return True if len(resArr) == 2 and resArr[0] == resArr[1][::-1] else False

本题的难点是，难以从几个例题中抽象出本题的主旨。

[3] 557. 反转字符串中的单词 III【简单】

给定一个字符串，你需要反转字符串中每个单词的字符顺序，同时仍保留空格和单词的初始顺序。

示例 1:

输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc" 

注意：在字符串中，每个单词由单个空格分隔，并且字符串中不会有任何额外的空格。

# 一次提交
class Solution:
    def reverseWords(self, s: str) -> str:
        s_lst = list(s.split())
        s_new = []
        for i in s_lst:
            s_new.append(i[::-1])
        return " ".join(s_new)
# 二次提交
class Solution:
    def reverseWords(self, s: str) -> str:
        s_lst = list(s[::-1].split())
        s_lst.reverse()
        return " ".join(s_lst)

[4] 15. 三数之和【难】

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

在刷[这道题的过程中介于奔溃状态，好不容易处理好了 LeetCode 上的所有问题，但是，由于所写程序的时间复杂度超过了要求，还是没有执行成功。经过多番资料查找，对于列表较大的情况，往往双指针算法是最好的解决办法。

双指针：主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。双指针可以从不同的方向向中间逼近也可以朝着同一个方向遍历。

下面是找到的大佬的代码，供自己学习：

"""
使用双指针，一个指针指向值较小的元素，一个指针指向值较大的元素。
指向较小元素的指针从头向尾遍历，指向较大元素的指针从尾向头遍历。
如果两个指针指向元素的和 sum == target，那么得到要求的结果；
如果 sum > target，移动较大的元素，使 sum 变小一些；
如果 sum < target，移动较小的元素，使 sum 变大一些。
"""
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
                nums.sort()
        res =[]
        i = 0
        for i in range(len(nums)):
            if i == 0 or nums[i]>nums[i-1]:
                l = i+1
                r = len(nums)-1
                while l < r:
                    s = nums[i] + nums[l] +nums[r]
                    if s ==0:
                        res.append([nums[i],nums[l],nums[r]])
                        l +=1
                        r -=1
                        while l < r and nums[l] == nums[l-1]:
                            l += 1
                        while r > l and nums[r] == nums[r+1]:
                            r -= 1
                    elif s>0:
                        r -=1
                    else :
                        l +=1
        return res

[5] 215. 数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

代码实现

# 利用堆实现
import heapq
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        lst = heapq.nlargest(k,nums)
        return sorted(lst)[0]

[6]面试题24. 反转链表【中】

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

ListNode{val: 1, next: ListNode{val: 2, next: ListNode{val: 3, next: ListNode{val: 4, next: ListNode{val: 5, next: None}}}}}

限制：

0 <= 节点个数 <= 5000

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        preNode = None
        currNode = head
        while currNode:
            nextNode = currNode.next
            currNode.next = preNode
            preNode = currNode
            currNode = nextNode
        return preNode

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    """
        对于所有的步骤，相当于一分为二的一个迭代过程first,second
        外加一个中间存储介质memory
    """
    def reverseList(self, head: ListNode) -> ListNode:
        first, memory = None, head  # 看作第一次切分，前一步分first为None,有一部分暂时给他放在memeory中
        while memory != None:
            second = memory.next    # 新的一次切分
            memory.next = first     # 将旧的加入first到新的中first中
            first = memory
            memory = second         # 为下一次切分做准备，同时作为判断条件，当切分到最后时，只有[1,2,3,4,5]与None
        return first

[7]3. 无重复字符的最长子串【难】

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        st = {}             
        # st字典用于存放字符串中各个字母的位置的下一个位置，
        # 如果出现重复字母时，从前面的子串中找到与该字母重复的字母的位置
        # 同时将该查找到重复字母的下一个位置作为下一个子串的起始位置
        i, ans = 0, 0       # i，起始位置；
        for j in range(len(s)):     # j，末位置
            if s[j] in st:
                i = max(st[s[j]], i)
            ans = max(ans, j - i +1 )   # ans，遍历过程中子串的最大长度；
            st[s[j]] = j + 1            # st字典用于存放字符串中各个字母的位置的下一个位置，
        return ans;

[7附加]面试题51. 数组中的逆序对【困难】

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

class Solution:
    def reversePairs(self, nums: List[int]) -> int:

        """利用归并排序merge思想，每个即将merge的数组是有序的来判断前大后小的种类个数"""
        self.res = 0
        self.merge_sort(nums, 0, len(nums) - 1)
        return self.res

    def merge_sort(self, nums, l, r):
        """左闭右闭"""
        if l >= r:
            return
        mid = l + (r - l) // 2
        self.merge_sort(nums, l, mid)
        self.merge_sort(nums, mid + 1, r)
        self.merge(nums, l, mid, r)

    def merge(self, nums, l, mid, r):
        aux = nums[l: r + 1]
        idx1, idx2 = l, mid + 1
        for k in range(l, r + 1):
            if idx1 > mid:
                nums[k] = aux[idx2 - l]
                idx2 += 1
            elif idx2 > r:
                nums[k] = aux[idx1 - l]
                idx1 += 1
            elif aux[idx1 - l] <= aux[idx2 - l]:
                nums[k] = aux[idx1 - l]
                idx1 += 1
            else:
                # 此时是大于的条件
                self.res += mid - idx1 + 1
                nums[k] = aux[idx2 - l]
                idx2 += 1

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        later_p=head
        poineer_p=head
        while n :
            n-=1
            poineer_p=poineer_p.next
        if poineer_p==None:
            head=head.next
            return head
        while poineer_p.next!=None:
            poineer_p=poineer_p.next
            later_p=later_p.next
        later_p.next=later_p.next.next
        return head

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        self.count = 0
        def merge(lfrom, lto, low, mid, high):
            '''
            lfrom:要归并的表
            lto:要存入的表
            low:归并段的开始
            mid:归并段中间
            high:归并段结束'''
            i, j, k = low, mid, low
            while i < mid and j < high: # 反复复制两分段首记录中较小的
                if lfrom[i] <= lfrom[j]:
                    lto[k] = lfrom[i]
                    i += 1
                    k += 1
                else:
                    lto[k] = lfrom[j]
                    self.count += mid - i
                    j += 1
                    k += 1
            while i < mid: # 复制第一段剩余记录
                lto[k] = lfrom[i]
                i += 1
                k += 1
            while j < high: # 复制第二段剩余记录
                lto[k] = lfrom[j]
                j += 1
                k += 1

        def merge_pass(lfrom, lto, llen, slen):
            '''
            llen:表长度
            slen:分段长度
            '''
            i = 0
            while i+2*slen < llen: # 归并这两段
                merge(lfrom, lto, i, i+slen, i+2*slen)
                i += 2*slen
            if i+slen < llen: # 后端长度不足slen
                merge(lfrom, lto, i, i+slen, llen)
            else: # 只剩下一段的情况，整段复制过去
                for j in range(i, llen):
                    lto[j] = lfrom[j]

        def merge_sort(lst):
            slen, llen = 1, len(lst)
            templst = [None]*llen
            while slen < llen:
                merge_pass(lst, templst, llen, slen)
                slen *= 2
                merge_pass(templst, lst, llen, slen) # 每一次都让结果存回原位
                slen *= 2
            return self.count
        return merge_sort(nums)

[8] 148. 排序链表【中等】递归

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:

输入: 4->2->1->3
输出: 1->2->3->4

示例 2:

输入: -1->5->3->4->0
输出: -1->0->3->4->5

示例代码：

class Solution:
    def sortList(self, head: ListNode) -> ListNode:
        # [1,3,2,4,6,5,7]
        if not head or not head.next:return head
        mid = self.getmid(head)
        rhead ,mid.next= mid.next,None # [6,5,7],[4]
        return self.mergesort(self.sortList(head),self.sortList(rhead))
    def getmid(self,head):
        # 双指针,slow = [1,2,3]
        if not head:return head
        slow = fast = head
        while fast.next and fast.next.next:fast,slow = fast.next.next,slow.next     
        return slow
    def mergesort(self,lhead,rhead):
        dummy = cur = ListNode(0)
        while lhead and rhead:
            if lhead.val <= rhead.val:cur.next,lhead  = lhead,lhead.next 
            else:cur.next ,rhead= rhead,rhead.next 
            cur = cur.next
        cur.next = lhead or rhead
        return dummy.next

[8附加]23. 合并K个排序链表【困难】递归

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if not lists:return 
        n = len(lists)
        return self.merge(lists, 0, n-1)
    def merge(self,lists, left, right):
        if left == right:
            return lists[left]
        mid = left + (right - left) // 2
        l1 = self.merge(lists, left, mid)
        l2 = self.merge(lists, mid+1, right)
        return self.mergeTwoLists(l1, l2)
    def mergeTwoLists(self,l1, l2):
        if not l1:return l2
        if not l2:return l1
        if l1.val < l2.val:
            l1.next = self.mergeTwoLists(l1.next, l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1, l2.next)
            return l2

[9]82. 删除排序链表中的重复元素 II

给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现 的数字。

示例 1:

输入: 1->2->3->3->4->4->5
输出: 1->2->5

示例 2:

输入: 1->1->1->2->3
输出: 2->3

示例代码：

class Solution(object):
    def deleteDuplicates(self, head):
        if head==None or head.next==None:
            return head
        # 构建一个字典，并且记录每个字母在字符串中出现的个数  
        dict1=dict()
        p1=head
        while p1:
            if p1.val not in dict1:
                dict1[p1.val]=1
            else:
                dict1[p1.val]+=1
            p1=p1.next
        # 看看是否每个字符都重复，如果都重复，就没有必要去除了，也可以看成是找到第一个没重复的元素位置
        # 如果都重复了，也就会出现下一步骤的head == None
        p1=head
        while p1:
            if dict1[p1.val]>1:
                p1=p1.next
            else:
                break
        # 由于第一个就没重复，所以从第一个开始
        head=p1
        if head==None:
            return head # 故障排除，不是通过break结束循环的，用于[1,1,2,2,3,3]
        if head.next==None: # 故障排除，[1,1,2,2,3]
            if dict1[head.val]>1:   # 感觉这个步骤用不上，经试验，确实没用
                return None
            else:
                return head
        # 上面的两种情况已处理，对于一般情况，如[1,2,3,3,4,4,5]
        p1=head     # [1,2,3,3,4,4,5]
        p2=head.next  # [2,3,3,4,4,5]
        # p1 与 p2相当于快慢指针，一前一后，用后面的指针来确定何时终止
        while 1:
            if dict1[p2.val]>1:
                p2=p2.next
                p1.next=p2  # 此处p2后移，p1不动
            else:
                p1=p1.next
                p2=p2.next
            if p2==None:
                return head     # 此处，通过p1更新head

[9附加]19. 删除链表的倒数第N个节点【中等】

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

示例代码：

class Solution:
    ## 很巧妙的双指针
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        a = head
        b = head
        for i in range(n):
            if a.next :
                a = a.next
            else:
                return head.next
        while a.next:
            a = a.next
            b = b.next
        b.next = b.next.next
        return head

[10]面试题35. 复杂链表的复制【中等】递归

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 1：

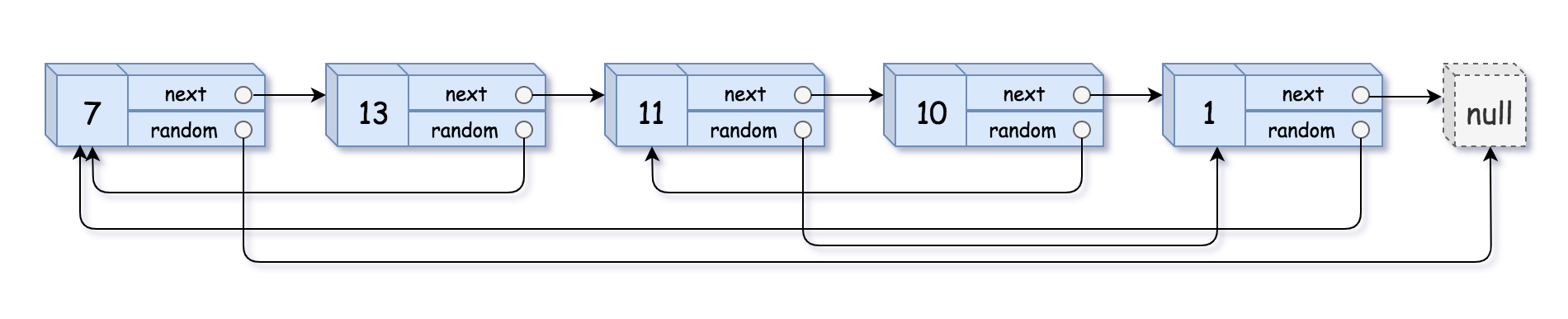
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

示例 4：

输入：head = []
输出：[]
解释：给定的链表为空（空指针），因此返回 null。

提示：

• -10000 <= Node.val <= 10000
• Node.random 为空（null）或指向链表中的节点。
• 节点数目不超过 1000 。

示例代码：

# 深度优先搜索
class Solution:
    def copyRandomList(self, head: 'Node') -> 'Node':
        def dfs(head):
            if not head: return None
            if head in visited:
                return visited[head]
            # 创建新结点
            copy = Node(head.val, None, None)
            visited[head] = copy    # 新旧之间的对应关系
            copy.next = dfs(head.next)
            copy.random = dfs(head.random)  # 字典似乎是为random建立的，可以反向搜索
            return copy
        visited = {}    # 放不同的节点
        return dfs(head)    # 返回最外层的

# 广度优先搜索
class Solution:
    def copyRandomList(self, head: 'Node') -> 'Node':
        visited = {}
    
        def bfs(head):
            if not head: return head
            clone = Node(head.val, None, None) # 创建新结点
            queue = collections.deque()
            queue.append(head)
            visited[head] = clone
            while queue:
                tmp = queue.pop()
                if tmp.next and tmp.next not in visited:
                    visited[tmp.next] = Node(tmp.next.val, [], [])
                    queue.append(tmp.next)  
                if tmp.random and tmp.random not in visited:
                    visited[tmp.random] = Node(tmp.random.val, [], [])
                    queue.append(tmp.random)
                visited[tmp].next = visited.get(tmp.next)
                visited[tmp].random = visited.get(tmp.random)
            return clone
        return bfs(head)

[10附加]138. 复制带随机指针的链表【中等】

给定一个链表，每个节点包含一个额外增加的随机指针，该指针可以指向链表中的任何节点或空节点。

要求返回这个链表的 深拷贝。

我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

• val：一个表示 Node.val 的整数。
• random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

示例 1：

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

示例 4：

输入：head = []
输出：[]
解释：给定的链表为空（空指针），因此返回 null。

提示：

• -10000 <= Node.val <= 10000
• Node.random 为空（null）或指向链表中的节点。

class Solution:
    def copyRandomList(self, head: 'Node') -> 'Node':
        def dfs(head):
            if not head: return None
            if head in visited:
                return visited[head]
            # 创建新结点
            copy = Node(head.val, None, None)
            visited[head] = copy    # 新旧之间的对应关系
            copy.next = dfs(head.next)
            copy.random = dfs(head.random)  # 字典似乎是为random建立的，可以反向搜索
            return copy
        visited = {}    # 放不同的节点
        return dfs(head)    # 返回最外层的

[11]110. 平衡二叉树

难度简单252收藏分享切换为英文关注反馈

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   /   9  20
    /     15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1
      /      2   2
    /    3   3
  /  4   4

返回 false 。

示例代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    # 可以从叶子到根节点反着理解
    def isBalanced(self, root: TreeNode) -> bool:
        def height(root):
            if root == None: return 0   # 临界条件
            lh = height(root.left)
            rh = height(root.right)
            if lh >= 0 and rh >= 0 and abs(lh-rh) <= 1:
                return max(lh,rh)+1
            else:
                return -1

        return height(root)>=0

[11附加题]面试题07. 重建二叉树【中等】

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

    3
   /   9  20
    /     15   7

限制：

0 <= 节点个数 <= 5000

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def re_construct_BTree(preorder,inorder):
            # 前序遍历和中序遍历长度一致
            if len(preorder) != len(inorder) or len(preorder)<1:
                return None
            if len(preorder) == 1:
                return TreeNode(preorder[0],None,None)
            root_node = preorder[0]
            root_tree = TreeNode(root_node)

            in_root_node_index = inorder.index(root_node)

            # 左子树
            pre_l_child_tree = preorder[1:in_root_node_index+1]
            in_l_child_tree = inorder[:in_root_node_index]
            root_tree.left = re_construct_BTree(pre_l_child_tree, in_l_child_tree)
            
            # 右子树
            pre_r_child_tree = preorder[in_root_node_index+1:]
            in_r_child_tree = inorder[in_root_node_index+1:]
            root_tree.right = re_construct_BTree(pre_r_child_tree, in_r_child_tree)
            
            return root_tree

[12]面试题27. 二叉树的镜像【简单】

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

     4
   /     2     7
 / \   / 1   3 6   9

镜像输出：

     4
    /    7   2
 / \   / 9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

限制：

0 <= 节点个数 <= 1000

示例代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        def cross_tree(root):
            if root == None: return None
            if root.left == None and root.right == None:
                return TreeNode(root.val)
            new_tree = TreeNode(root.val)
            new_tree.left = cross_tree(root.right)
            new_tree.right = cross_tree(root.left)
            return new_tree 
        return cross_tree(root)
    

执行用时 :64 ms, 在所有 Python3 提交中击败了8.37%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了100.00%的用户

主要问题在于，创建了一个函数；而且完成了对树的深拷贝，本题中我们只需要在原来的基础上修改就好。

更新代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if root == None: return None
        root.left,root.right = root.right, root.left 
        self.mirrorTree(root.left)
        self.mirrorTree(root.right)
        return root

执行用时：32 ms
内存消耗：13.6 MB

[12附加]面试题26. 树的子结构[中等]

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

3 / \ 4 5 / \ 1 2
给定的树 B：

4 / 1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        if B == None: return False
        if A == None: return False
        # 经过这两个条件的筛选，A,B两棵树的不可能为None
        # 下面需要考虑子结构为None的情况
        def helper(a,b):
            # 仅仅是子结构b == None的情况，
            if b == None: return True
            if a == None: return False
            if a.val == b.val:
                if helper(a.left,b.left) and helper(a.right,b.right): return True
            if B == b:
                if helper(a.left,b) or helper(a.right,b): return True
            return False
        return helper(A,B)

执行用时 :192 ms, 在所有 Python3 提交中击败了14.01%的用户
内存消耗 :18 MB, 在所有 Python3 提交中击败了100.00%的用户

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        def ismatch(A,B):
            # 对比left和right
            if A == None or A.val != B.val: return False
            return (B.left == None or ismatch(A.left,B.left)) and (B.right == None or ismatch(A.right,B.right))
        
        
        if A == None and B == None: return True
        if A == None or B == None:  return False
        if A.val == B.val and ismatch(A,B): 
            return True
        else:
            return self.isSubStructure(A.right,B) or self.isSubStructure(A.left,B)

执行用时 :156 ms, 在所有 Python3 提交中击败了32.10%的用户
内存消耗 :17.7 MB, 在所有 Python3 提交中击败了100.00%的用户

[13]面试题32 - I. 从上到下打印二叉树【中等】

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   /   9  20
    /     15   7

返回：

[3,9,20,15,7]

提示：

1. 节点总数 <= 1000

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

from queue import Queue
class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
        if root == None: return []
        queue = Queue()
        queue.put(root)
        res = []
        while queue.empty() == False:
            node = queue.get()  # get相当于列表中的pop
            res.append(node.val)
            if node.left:
                queue.put(node.left)    # 可能是棵树，也可能是个数
            if node.right:
                queue.put(node.right)
        return res

本代码或者说本题的一个思路就是，将Tree逐渐细分，[root, root.left, root.right, root.left.left, root.left.right, ... ]，其中的每个元素是一棵树，如果将他这么细分下去，那么我们只需要得到每个元素（树）的val值，并将其插入列表就可实现本题的功能。

执行用时 :44 ms, 在所有 Python3 提交中击败了48.76%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了100.00%的用户

[13附加题]面试题32 - III. 从上到下打印二叉树 III【中等】

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   /   9  20
    /     15   7

返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]

提示：

1. 节点总数 <= 1000

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        reverseFlag = False
        queue = [root]
        res_lst = []
        while queue:
            nextQueue = []  
            # 由于nextQueue是要用来为下一次的遍历做准备，而且，同一层的节点在一个[]
            # 因此要放入同一个循环中
            valueQueue = []
            for node in queue:
                if not node:
                    continue
                nextQueue.append(node.left)
                nextQueue.append(node.right)
                valueQueue.append(node.val)
            queue = nextQueue
            if reverseFlag:
                valueQueue = valueQueue[::-1]
            reverseFlag = not reverseFlag
            if valueQueue:
                res_lst.append(valueQueue)
        return res_lst

[14] 面试题34. 二叉树中和为某一值的路径【中等】

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 sum = 22，

              5
             /             4   8
           /   /           11  13  4
         /  \    /         7    2  5   1

返回:

[
   [5,4,11,2],
   [5,8,4,5]
] 

提示：

1. 节点总数 <= 10000

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
        ans, path = [],[]
        def dfs(root, sum):
            if not root: return
            path.append(root.val)   
            sum -= root.val
            if not root.left and not root.right and not sum:
                # not sum以为这在叶子结点处是否将sum减小至0
                ans.append(path[:])
            dfs(root.left, sum)     
            dfs(root.right, sum)
            path.pop()
            # 对于path，并非属于并行，递归他也有前后顺序的
            # 按照例子，首先path中的元素为[5,4,11,7],之后由于sum不为0，未将path插入ans中
            # 也就是在root=7的时候，dfs(root.left, sum) 和 dfs(root.right, sum)执行
            # 并且什么都不返回，之后执行path.pop(),那么path就变成[5,4,11]
            # 之后root退回到11，此时，root==1中dfs(root.left, sum)已经完成，开始执行
            # dfs(root.right, sum)，root.right == 2，同时递归到下一轮，path变为[5,4,11,2]
        
        dfs(root, sum)
        return ans

执行用时 :52 ms, 在所有 Python3 提交中击败了68.81%的用户

内存消耗 :15.1 MB, 在所有 Python3 提交中击败了100.00%的用户

[14附加题]124. 二叉树中的最大路径和【困难】

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      /      2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   /   9  20
    /     15   7

输出: 42

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def dfs_sum(self, root: TreeNode):
        # 一个分支
        if root == None: return 0
        val = root.val
        sum_l = max(0, self.dfs_sum(root.left))     # 此处的0就是不把小于0的分支加进去
        sum_r = max(0, self.dfs_sum(root.right))
        self.ans = max(self.ans, sum_l + sum_r + val)
        return  max(sum_l , sum_r) + val
    
    def maxPathSum(self, root: TreeNode) -> int:
        self.ans = -1e9 # 防止只有一个元素且为负，self.ans代表的是遍历的树中的最大值
        self.dfs_sum(root)
        return self.ans

执行用时 :140 ms, 在所有 Python3 提交中击败了21.54%的用户

内存消耗 :20.2 MB, 在所有 Python3 提交中击败了51.79%的用户

[15] 98. 验证二叉搜索树【中等】

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   /   1   3
输出: true

示例 2:

输入:
    5
   /   1   4
     /     3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

1 递归，中序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        res = []
        def helper(root):
            if not root:
                return 
            helper(root.left)
            res.append(root.val)
            helper(root.right)
        helper(root)
        return res == sorted(res) and len(set(res)) == len(res)

执行用时 :56 ms, 在所有 Python3 提交中击败了47.26%的用户

内存消耗 :17 MB, 在所有 Python3 提交中击败了5.10%的用户

2 最大值最小值

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        def isBST(root, min_val, max_val):
            if root == None:
                return True
            # print(root.val)
            if root.val >= max_val or root.val <= min_val:
                return False
            return isBST(root.left, min_val, root.val) and isBST(root.right, root.val, max_val)
        return isBST(root, float("-inf"), float("inf"))

[15附加题]面试题36. 二叉搜索树与双向链表【中等】

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

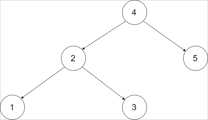
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

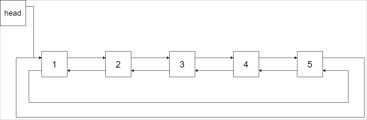
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

"""
# Definition for a Node.
class Node:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
"""
class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        
        if root is None:
            return None

        self.first = None
        self.last = None
        self.helper(root)
        self.first.left = self.last
        self.last.right = self.first
        return self.first

    def helper(self, root):
        # 此处的遍历方式为中序遍历，因此都是从小到大遍历的
        # 也就是访问的前一个节点是后一个节点的left
        # 有一个节点是前一个节点的right
        if root is None:
            return

        self.helper(root.left)

        if self.last is not None:
            root.left = self.last
            self.last.right = root # 虽然进行该操作，但都是对root的修改
        else:
            self.first = root  # 只会发生一次
        self.last = root

        self.helper(root.right)

执行用时 :60 ms, 在所有 Python3 提交中击败了25.11%的用户

内存消耗 :14.5 MB, 在所有 Python3 提交中击败了100.00%的用户

[16]面试题54. 二叉搜索树的第k大节点【简单】

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  /  1   4
     2
输出: 4

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      /      3   6
    /    2   4
  /
 1
输出: 4

限制：

1 ≤ k ≤ 二叉搜索树元素个数

示例代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
# 将二叉树中的每个元素放入列表，之后去其中第k大值
class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        lst = []
        def tree2list(root):
            if not root : return
            tree2list(root.left)
            lst.append(root.val)
            tree2list(root.right)
        tree2list(root)
        return lst[-k]

执行用时 :60 ms, 在所有 Python3 提交中击败了78.76%的用户

内存消耗 :17.5 MB, 在所有 Python3 提交中击败了100.00%的用户

[16附加题]98. 验证二叉搜索树

难度中等464

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   /   1   3
输出: true

示例 2:

输入:
    5
   /   1   4
     /     3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

示例代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        lst = []
        def tree2lst(root):
            if not root: return
            tree2lst(root.left)
            lst.append(root.val)
            tree2lst(root.right)

        tree2lst(root)
        return lst == sorted(lst) and len(set(lst)) == len(lst)

执行用时 :56 ms, 在所有 Python3 提交中击败了47.56%的用户

内存消耗 :16.9 MB, 在所有 Python3 提交中击败了5.00%的用户

[17]111. 二叉树的最小深度

难度简单229收藏分享切换为英文关注反馈

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

    3
   /   9  20
    /     15   7

返回它的最小深度 2.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0
        l_depth = self.minDepth(root.left)
        r_depth = self.minDepth(root.right)
        return min(l_depth,r_depth) + 1 if (l_depth and r_depth) else 1+l_depth + r_depth
    # 本题的关键就是，如果一个节点的左、右子树中只有一个存在，那么就用存在的那个，如果都没有就没有咯

执行用时 :84 ms, 在所有 Python3 提交中击败了8.42%的用户

内存消耗 :15.4 MB, 在所有 Python3 提交中击败了5.22%的用户

[17附加题]130. 被围绕的区域【中等】

给定一个二维的矩阵，包含 ‘X‘ 和 ‘O‘（字母 O）。

找到所有被 ‘X‘ 围绕的区域，并将这些区域里所有的 ‘O‘ 用 ‘X‘ 填充。

示例:

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O‘ 都不会被填充为 ‘X‘。 任何不在边界上，或不与边界上的 ‘O‘ 相连的 ‘O‘ 最终都会被填充为 ‘X‘。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

class Solution:
    def solve(self, board: List[List[str]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        def dfs(board,i,j):
            if i<0 or j<0 or i>=row_num or j >= column_num or board[i][j] == "X" or board[i][j] == "#":
                return
            board[i][j] = "#"
            dfs(board, i - 1, j); # 上
            dfs(board, i + 1, j); # 下
            dfs(board, i, j - 1); # 左
            dfs(board, i, j + 1); # 右 
            # 只要和最外侧的O相连，不论是直接相连，还是中间隔了个O，都算相连，要处理
            # 那么，对于里面的，只要判断他就行了，没有必要看周围了
            
        
        
        if board == None or len(board) == 0: return
        row_num = len(board)
        column_num = len(board[0])
        for i in range(row_num):
            for j in range(column_num):
                isEdge = i == 0 or j == 0 or i == row_num - 1 or j == column_num - 1
                if isEdge and board[i][j] == "O":
                    dfs(board,i,j)

        for i in range(row_num):
            for j in range(column_num):
                if board[i][j] == "O":
                    board[i][j] = "X"

                if board[i][j] == "#":
                    board[i][j] = "O"

执行用时 :84 ms, 在所有 Python3 提交中击败了78.10%的用户

内存消耗 :14.7 MB, 在所有 Python3 提交中击败了20.73%的用户

LeetCode日常刷题

标签：poi   平衡   array   cte   bool   image   超过   区间   min   

原文地址：https://www.cnblogs.com/damin1909/p/12527146.html