二叉树

标签：后序   http   tree   查找   遍历   rar   最大值   其它   层次遍历   

      一棵二叉树是结点的一个有限集合,该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

二叉树性质：

1. 若二叉树的层次从0开始，则在二叉树的第i层最多有2^i 个结点。(i>= 0) (证明用数学归纳法)。
2. 高度为k的二叉树最多有2^(k+1)-1个结点。 (k>= -1) (证明用求等比级数前 k项和的公式)。
3. 对任何一棵二叉树,如果其叶结点个数为n0,度为2的非叶结点个数为n2,则有n0=n2+ 1。

满二叉树(Full Binary Tree):每一 个层的结点数都达到最大值，则这个二叉树就是满二叉树。

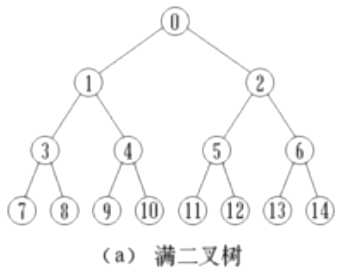
完全二叉树(Complete Binary Tree):若设二叉树的高度为h,则共有h+1层。除第h层外，其它各层(0 ~ h-1)的结点数都达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。

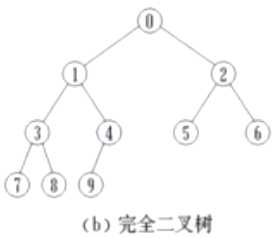
注意：局部满足满二叉树或完全二叉树的性质，不能说该树就是满二叉树或完全二叉树。

具有n个节点的完全二叉树其高度为log₂(n+1) - 1。

推导如下：

设完全二叉树的高度为h，则有2^h - 1 < n ≤ 2^h+1- 1  ^→ 2^h < n+1 ≤ 2^h+1 → 取对数 h < log₂(n+1) ≤  h+1。

二叉树链表表示：

• 二叉链表

• 三叉链表

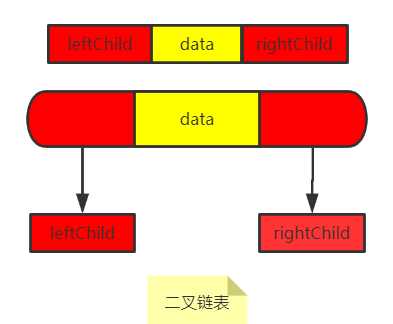
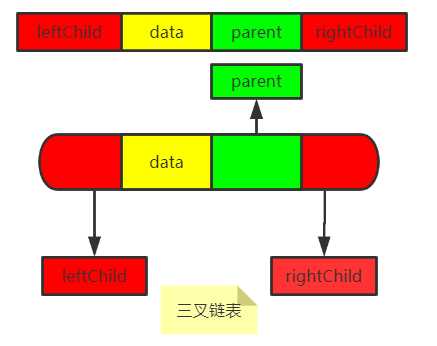
 三叉链表查找更快，但是需要的内存更多。

二叉树的遍历：（深度优先遍历）         （层次遍历，为广度优先遍历）

前序遍历： 若二叉树为空，则结束; 否则  访问根结点(V);前序遍历左子树(L);前序遍历右子树(R)。

中序遍历： 若二叉树为空，则结束; 否则  中序遍历左子树(L);访问根结点(V);中序遍历右子树(R)。

后序遍历： 若二叉树为空，则结束; 否则  后序遍历左子树(L);后序遍历右子树(R);访问根结点(V)。

二叉树

标签：后序   http   tree   查找   遍历   rar   最大值   其它   层次遍历   

原文地址：https://www.cnblogs.com/128-cdy/p/12521106.html