标签:相同 mic block 情况 执行 display http 关系 创建
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ 2 6
/ 1 3
示例 1:
输入: [1,6,3,2,5] 输出: false
示例 2:
输入: [1,3,2,6,5] 输出: true
提示:
数组长度 <= 1000首先作为二叉排序树的后序遍历来说,最后输出的为根节点。以下二叉排序树为例讲解,其输出的后序遍历为
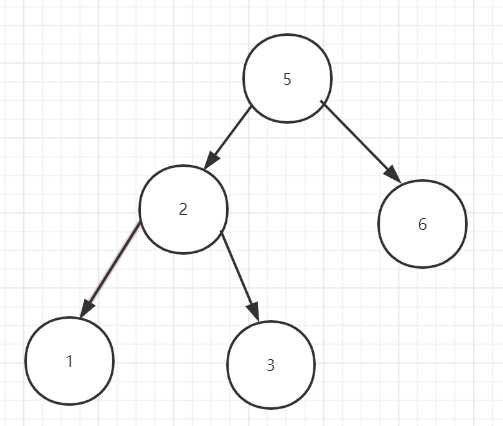
[1,3,2,6,5],如果该序列要满足是二叉树排序的后序遍历要求,则应该每一个节点的左子树小于该节点,有子树大于该节点的值,这样子才能确定是不是后序遍历,既要满足后序遍历的要求,又要满足二叉排序树的要求。
思路流程:
递归三要素:
class Solution { int[] postOrder = null; public boolean verifyPostorder(int[] postorder) { postOrder = postorder; return recur(0,postOrder.length-1); } //递归方法,判断当前区间序列是不是二叉排序树的后序遍历 //本轮递归终止条件:i>=j时,意味着当前区间缩小成为为0,则应该直接return true。退出本次递归 //递归逻辑:首先把当前区间划分为左右子树的位置,然乎判断是不是左子树都小于根节点,右子树大于根节点 //如果满足,则继续以当前左右子树区间继续递归,判断,否则直接return false。直到所有节点的左右子树都满足二叉排序树才行。 //递归返回值:当且仅当当前区间左右子树都为二叉树后序遍历时才能return true public boolean recur(int i,int j){ //本轮终止条件 if(i>=j) return true; int m=i;//初始值为i,记录当前左右子树的划分点位置。 //寻找左右子树划分点 while(true){ //如果当前i位置的值一旦大于尾部的根节点,则找到了划分左右子树的节点位置,break即可 if(postOrder[m]>=postOrder[j]){ break; } m++; } //则此时,[i,m-1]为左子树区间,[m,j-1]为右子树区间,j为根节点。 //接下来判断该左右子树划分点,是不是满足左子树都小于根节点,右子树都大于根节点 //由于我们再求得m位置时,就是通过小于根节点的条件求得的,所以可以直到所有左子树都是小于根节点的。 //下面判断是不是所有右子树都大于根节点尼? int a = m; while(true){ //如果到了j位置,依然满足大于根节点,则break,继续执行。 if(a==j){ break; } //一旦出现小于根节点的情况,则直接return fasle代表当前区间不是二叉排序树的后序遍历序列 if(postOrder[a]<postOrder[j]){ return false; } else{ a++; } } //经过前面的判断,知道当前区间是满足二叉排序树的后序遍历,所以开始向其内部的子节点判断是不是二叉排序树的后序遍历 return recur(i,m-1)&&recur(m,j-1); } }
小小心得:对于这种递归返回值是boolean类型的递归方法。所有return false的情况都可以单独列出来,而为了return true的条件假设又多个,则可以通过return s1&&s2&&s3&&s4......等等将所有的条件向与,其含义是指当所有这些条件都满足时,才能return true!当其中一个条件不能满足是,return false。当然你也可以这样写,将所有情况的分别判断是直接return false,还是可以继续判断后序条件,这样写的逻辑没问题,但是比较繁琐了,冗长!!加油。
标签:相同 mic block 情况 执行 display http 关系 创建
原文地址:https://www.cnblogs.com/dazhu123/p/12529872.html