标签:操作 步骤 初始化 拓扑 pre 文件中 path NPU res
腰酸背痛一个上午,终于搞定了。。
一 用到二个工具:
1.回溯法的算法思想
2.顺序表(主要用到了删除操作)
二 程序设计步骤:
1.读入图;
这里我没有用严格的图结构。而是用邻接矩阵来表示图,邻接矩阵放在一个txt文件中。(见后文)
读入图就是指读入这个文件。
2.计算图中顶点的入度;
用一个结构体数组来存放顶点名称和顶点的入度(我这里的结构体名称是ElemType)
3.初始化顺序表
这一步只需初始化第0号顺序表。。。
用2中的顶点入度数组来初试化。
4.开始计算拓扑序列
这里我们把图的每个顶点比作一个球,每个顺序表比作一个袋子。
假设图有十个顶点,则需要十个袋子。(100个顶点,需要100个袋子。。。)
这个问题与常见回溯算法不同的一个特点:从前一个袋子里取出球后,才能知道下一个袋子里装的是那几个球。
思想如下:
(1)将所有的球装入第0号袋子;
(2)从袋子中取出一个球。如果合法(即入度为0),进行下一步;如果非法(即入度不为0),取下一个球。
(3)根据(2)中取出的球,计算下一个袋子中的球的情况。上一步袋子中的球,除去取出的球外,全部放入下一个袋子(假设为A号袋子)中。根据取出的球(即顶点),
计算A号袋子中球(即顶点)的入度。
(4)重复步骤(2),每次袋子中都会少一颗球,直到最后一个袋子。取球的顺序即该图的一个拓扑排序;
(5)从最后一个袋子开始回溯,直到回到第0号袋子,并把第0号袋子中的球取完为止。
5.输出
三 示例
1.需要拓扑排序的图
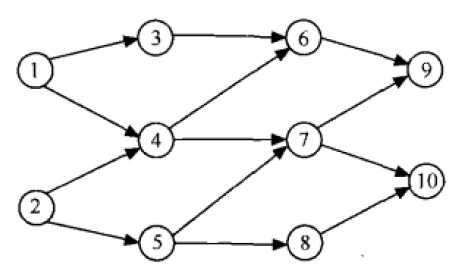
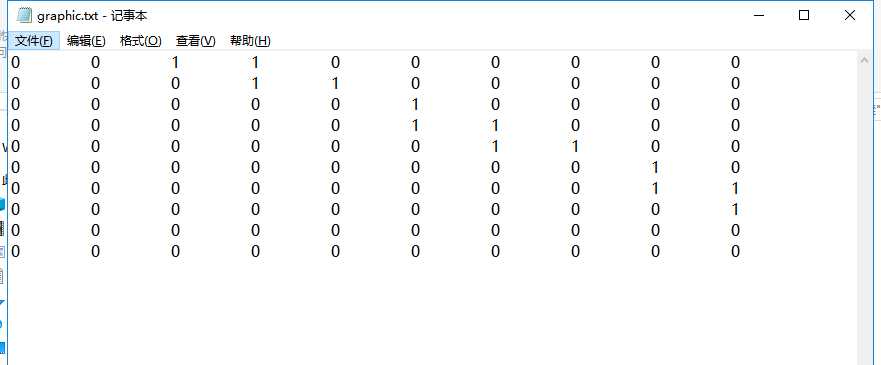
2.存放邻接矩阵的文件。。
3.代码
(1)我的一个存放顺序表操作的头文件。。
1 #pragma once 2 #ifdef ElemType 3 #else 4 #define ElemType int 5 #endif 6 #ifdef MaxSize 7 #else 8 #define MaxSize 10 9 #endif 10 11 //顺序表 12 struct sqList 13 { 14 ElemType data[MaxSize]; 15 int length; 16 }; 17 typedef struct sqList SqList; 18 19 //初始化 20 void init(SqList* list) 21 { 22 list->length = 0; 23 return; 24 } 25 26 //求长度 27 int getLength(SqList* list) 28 { 29 return list->length; 30 } 31 32 //插入 33 int insert(SqList* list, int n, ElemType x) 34 { 35 if (list->length >= MaxSize || n < 0 || n > list->length) 36 { 37 return 0; 38 } 39 int i = list->length; 40 while (i > n) 41 { 42 list->data[i] = list->data[i - 1]; 43 i--; 44 } 45 list->data[n] = x; 46 list->length++; 47 return 1; 48 } 49 50 //删除 51 int del(SqList* list, int n, ElemType* x) 52 { 53 if (n < 0 || n > list->length - 1) 54 { 55 return 0; 56 } 57 int i = n; 58 *x = list->data[i]; 59 while (i < list->length - 1) 60 { 61 list->data[i] = list->data[i + 1]; 62 i++; 63 } 64 list->length--; 65 return 1; 66 }
(2)开始求拓扑排序
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 struct elemType 5 { 6 int name; //顶点名称 7 int num; //顶点的入度数 8 }; 9 #define ElemType elemType 10 #define MaxSize 10 11 #define ROW 10 12 #define COL 10 13 #include"sq-list.h" 14 15 SqList bags[COL + 1]; //袋子 16 17 int inputGraphic(const char *path, int mGraphic[][COL], int row); 18 void getInDegree(int mGraphic[][COL], int row, ElemType degs[], int n); 19 void initList(ElemType degs[], int n); 20 int permulation(int mGraphic[][COL], int row, int n); 21 void printResult(int result[], int n); 22 23 24 int main() 25 { 26 const char* path = "graphic.txt"; 27 int mGraphic[ROW][COL]; 28 ElemType degs[COL]; //存放图中的顶点信息和入度数 29 int counter = 0; 30 31 if (!inputGraphic(path, mGraphic, ROW)) 32 { 33 return 0; 34 } 35 getInDegree(mGraphic, ROW, degs, COL); 36 initList(degs, COL); 37 counter = permulation(mGraphic, ROW, COL); 38 printf("这个图共有:%d种拓扑排序", counter); 39 return 0; 40 } 41 42 //读入图 43 int inputGraphic(const char* path, int mGraphic[][COL], int row) 44 { 45 int i, j; 46 FILE* fp; 47 fp = fopen(path, "r"); 48 if (fp == NULL) 49 { 50 return 0; 51 } 52 for (i = 0; i < ROW; i++) 53 { 54 for (j = 0; j < COL; j++) 55 { 56 fscanf(fp, "%d", &mGraphic[i][j]); 57 } 58 } 59 fclose(fp); 60 return 1; 61 } 62 63 //计算每个顶点的入度 64 void getInDegree(int mGraphic[][COL], int row, ElemType degs[], int n) 65 { 66 int i, j; 67 for (j = 0; j < COL; j++) 68 { 69 degs[j].name = j; 70 degs[j].num = 0; 71 for (i = 0; i < ROW; i++) 72 { 73 degs[j].num += mGraphic[i][j]; 74 } 75 } 76 } 77 78 //初始化顺序表 79 void initList(ElemType degs[], int n) 80 { 81 init(&bags[0]); 82 int i = 0, j = 0; 83 for (i = 0; i < n; i++) 84 { 85 bags[0].data[i] = degs[i]; 86 } 87 bags[0].length = n; 88 } 89 90 //计算所有拓扑排序 91 int permulation(int mGraphic[][COL], int row, int n) 92 { 93 int counter = 0; //计数器,即共多少种排序方式 94 int i = 0, j = 0; 95 int temp = 0; 96 ElemType ball, tempBall; 97 int* index = (int*)malloc(sizeof(int) * n); 98 int* result = (int*)malloc(sizeof(int) * n); 99 if (index == NULL || result == NULL) 100 { 101 return -1; 102 } 103 for (i = 0; i < n; i++) 104 { 105 index[i] = 0; 106 } 107 108 i = 0; 109 while (i >= 0) 110 { 111 //从第i号袋子中,取第index[i]号球 112 if (i < n) 113 { 114 if (bags[i].data[index[i]].num != 0) 115 { 116 //如果取出的球不合法(即度不为0),则取下一个球 117 index[i] += 1; 118 } 119 else if (index[i] >= bags[i].length) 120 { 121 //回溯 122 //当第i号袋子中所有的球都被取过之后,回溯到第i-1号袋子 123 //同时要把i~n-1号袋子"还原",即index[i]=0,index[i+1]=0... 124 //保证再次取到这个袋子时,依然时从0号球开始取 125 temp = i; 126 i--; 127 while (temp < n) 128 { 129 index[temp++] = 0; 130 } 131 } 132 else 133 { 134 //取出一颗球 135 result[i] = bags[i].data[index[i]].name; 136 //生成下一个袋子里的球 137 bags[i + 1] = bags[i]; 138 del(&bags[i + 1], index[i], &tempBall); 139 for (j = 0; j < bags[i + 1].length; j++) 140 { 141 ball = bags[i + 1].data[j]; 142 if (mGraphic[tempBall.name][ball.name] == 1) 143 { 144 bags[i + 1].data[j].num--; 145 } 146 } 147 //下次在从i号袋子里取球时,取index[i]+1号球 148 index[i] += 1; 149 //从下一个袋子里取球 150 i++; 151 } 152 } 153 else 154 { 155 counter++; 156 printResult(result, n); 157 i--; 158 } 159 } 160 161 return counter; 162 free(index); 163 free(result); 164 } 165 166 void printResult(int result[], int n) 167 { 168 int i = 0; 169 for (i = 0; i < n; i++) 170 { 171 //此处加1是因为图中顶点是从1开始编号的,而程序中顶点从0开始编号 172 printf("%d,", result[i] + 1); 173 } 174 printf("\n"); 175 }
标签:操作 步骤 初始化 拓扑 pre 文件中 path NPU res
原文地址:https://www.cnblogs.com/ben-/p/12531472.html