标签:robert 分离 htm att 推导 roc dict ini expect
在处理机器学习的分类问题中,我们需要评估分类结果的好坏以选择或者优化模型,本文总结二分类任务中常用的评估指标。对于多分类任务的评估指标,可以参考这篇文章
先从我们最熟知的混淆矩阵(confusion matrix)说起。
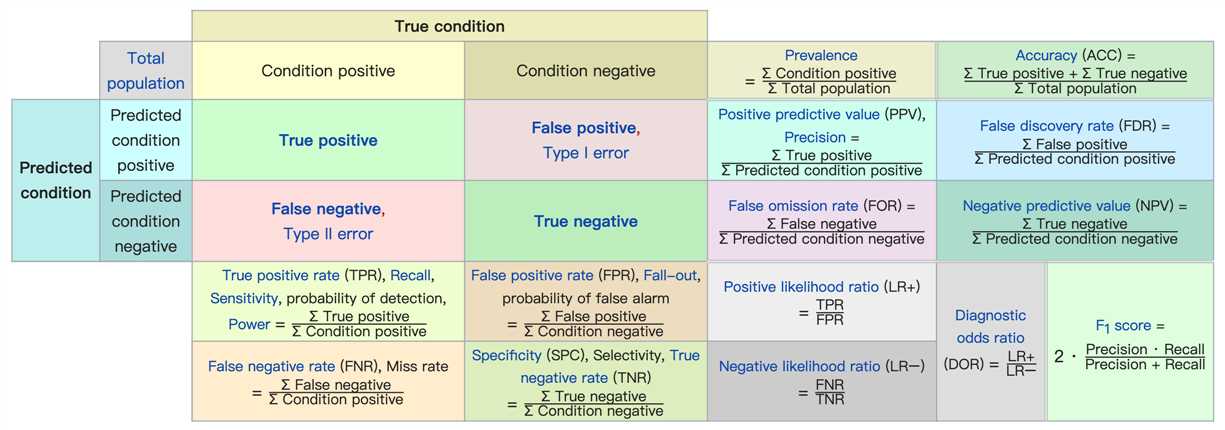
source
鉴于混淆矩阵看着比较抽象,可以参考下图
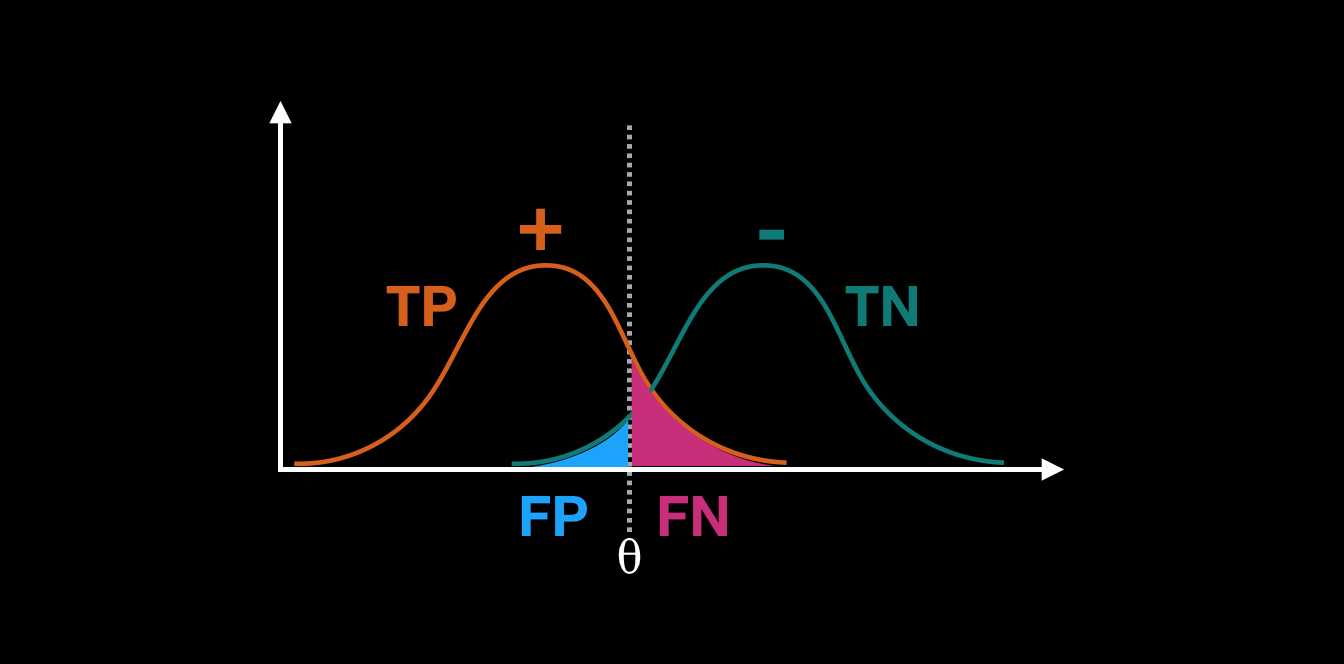
常用的评估指标可以分为3类:
错误率定义为分类错误的样本数占样本总数的比例
\[
Err = \frac{FP+FN}{N_{sample}}
\]
正确率(精度) 定义为分类正确的样本数占总数的比例
\[
Acc = 1-Err = \frac{TP+TN}{N_{sample}}
\]
注意:\(N_{sample}\)表示样本总数(即confusion matrix中TP, FP, TN, FN之和)。
Precision(准确率、查准率) ,即判断为正例的样本中有多大比例是真的正例。
\[P=\frac{TP}{TP+FP}\]
Recall(召回率、查全率) ,即正例样本中有多大比例的正例被发现(判定为正例),该指标也称为True Positive Rate(TPR)、Sensitivity.
\[R = \frac{TP}{TP+FN}\]
考虑到FP和FN的关系是I类错误和II类错误的关系,会此消彼长,故Precision和Recall也有这种关系。对比多个模型的表现时,可以用P-R图(横轴为Recall,纵轴为Precision).
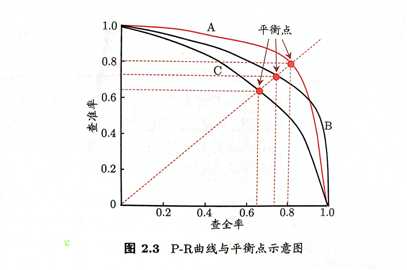
截图来自《机器学习》周志华,更多信息可以参考本书2.3节1.3
TPR(True Positive Rate) ,正例样本中被正确判定为正例的样本数比例,该指标也称为Sensitivity(敏感度)。
\[TPR = sensitivity = \frac{TP}{TP+FN}\]
TNR(True False Rate) ,指负例样本中被正确判定为负例的样本数比例,该指标也称为Specificity(特异度)。
\[TNR = specificity = \frac{TN}{TN+FP}\]
假设我们要判断人群中的好人(正例)和坏人(负例),如果我们的关注点是“不能冤枉好人”,那么就要尽可能把好人识别出来(判断为好人的标准趋于宽松,坏人也可能被识别为好人),此时的Precision会趋于更小,Recall会趋于更大;当我们关注的是“不能放过坏人”(比如风控业务中,“坏”客户造成的业务损失很大),此时判断好人的标准更加严格,更多的“真”好人会被纳入“嫌疑对象”(判定为负例),此时的Precision会趋于更大,但是Recall会降低;如果我们“尽可能既不能冤枉好人,又不能放过坏人”,那么就需要在Precision和Recall中取得平衡,此时可以看F1-Score上的表现(不过对于正负例样本不均衡的情况下,F1-Score表现并不好)。
F1-Score 是Precision和Recall的调和平均值,即
\[\frac{1}{F_1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})\]
由此可推导得到
\[
\begin{aligned}
F_1 & = \frac{2 \cdot P \cdot R}{P+R} \& = \frac{2TP}{2TP+FN+FP}
\end{aligned}
\]
更一般地,某些场景下关注Precision和Recall的权重不同!
\[\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})\]
当\(\beta>1\)时,Recall的权重更大,\(\beta<1\)时Precision的权重更大。
简称MCC(马修斯相关系数,Brian W. Matthews, 1975),
更多参考
\[
MCC = \frac{TP \times TN-FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FN)(TN+FP)}}
\]
从公式中可以看出MCC和2*2列联表的卡方检验很相近。MCC的值域为[-1,1].
MCC的好处是:
简称BCR,BCR为正例样本和负例样本中各自预测正确率的均值。
\[BCR=\frac{1}{2}(TPR+TNR)\]
与BCR对应的是BER(Balanced Error Rate),也称之为Half Total Error Rate(HTER).
\[BER = 1-BCR\]
同MCC一样,正负例的标签选择对BCR的计算没有影响,而且一定程度上也能克服正负例样本不均衡导致的评估指标虚高。
在分类模型中对样本归属类别的判断通常不是直接得到0或者1,而是一个连续的值区间(比如Logistic回归得到的预测值落在概率区间[0,1]),然后通过划定阈值来判断正例或者负例(比如概率\(p=0.5\)判定为正例)。
如果要看分类模型在不同决策阈值下的表现如何,则可以借助ROC曲线(Receiver Operating Characteristic Curve,受试者操作特征曲线) 。
ROC曲线中:
注:上面公式中的N、P是指负例样本和正例样本各自的样本数量。
将样本按预测为正例的概率从高到低进行排序后,依次计算每个概率值作为判定阈值对应的TPR和FPR,再将排序后的每个数据点的TPR和FDR值描点到坐标系中,就得到ROC曲线。如下图示,我们可以看到,将决策阈值往正例方向移动时,对应的TPR和FDR都会下降(FDR和TPR是正相关的关系,所以作ROC曲线图将样本按TPR从小到大排序时,FDR也是从小到大的顺序)。
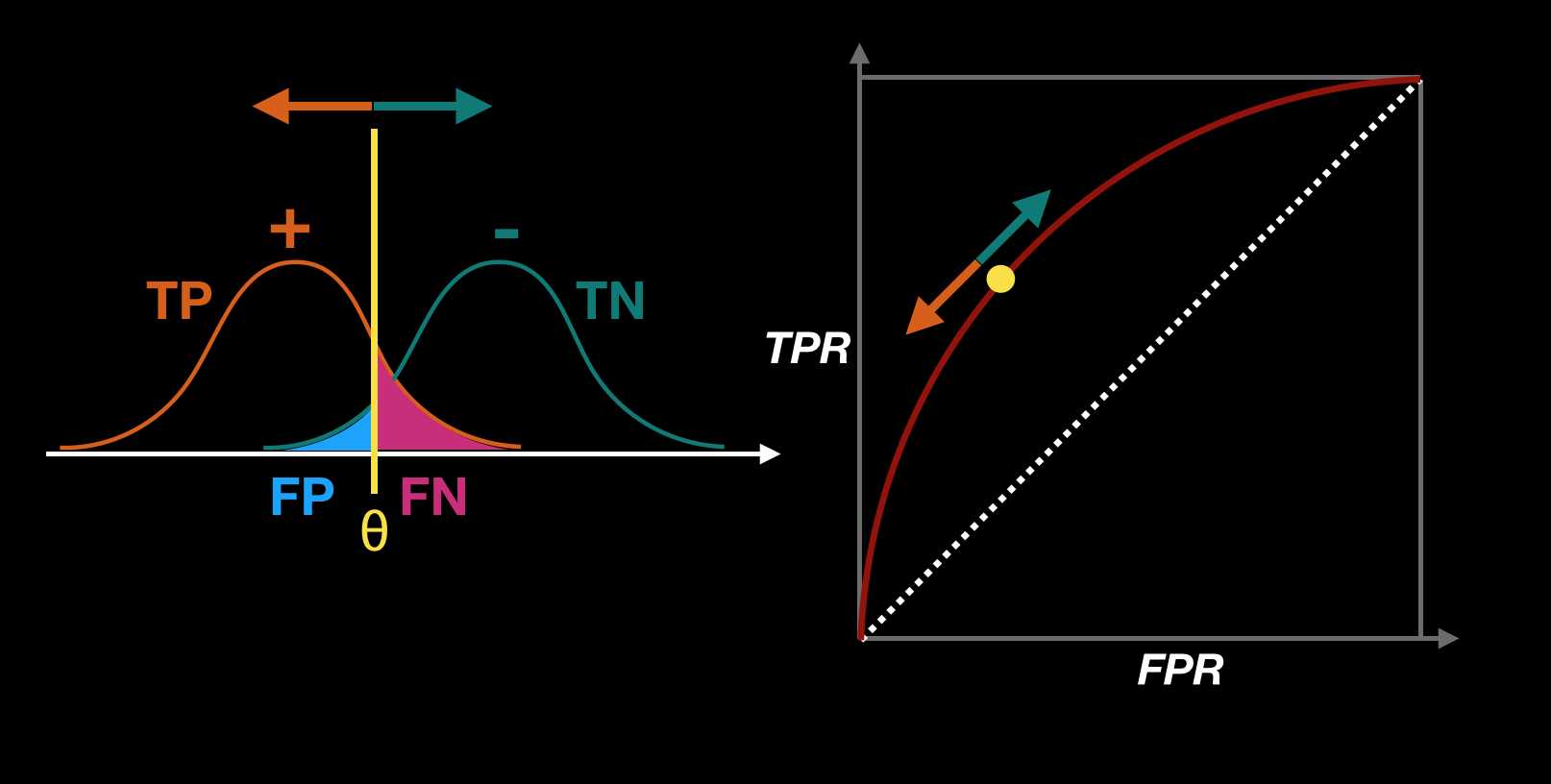
注:ROC曲线图中左下角到右上角的虚线表示“随机操作”下的值(作为参考线)
ROC中决策阈值变化的动态展示如下:
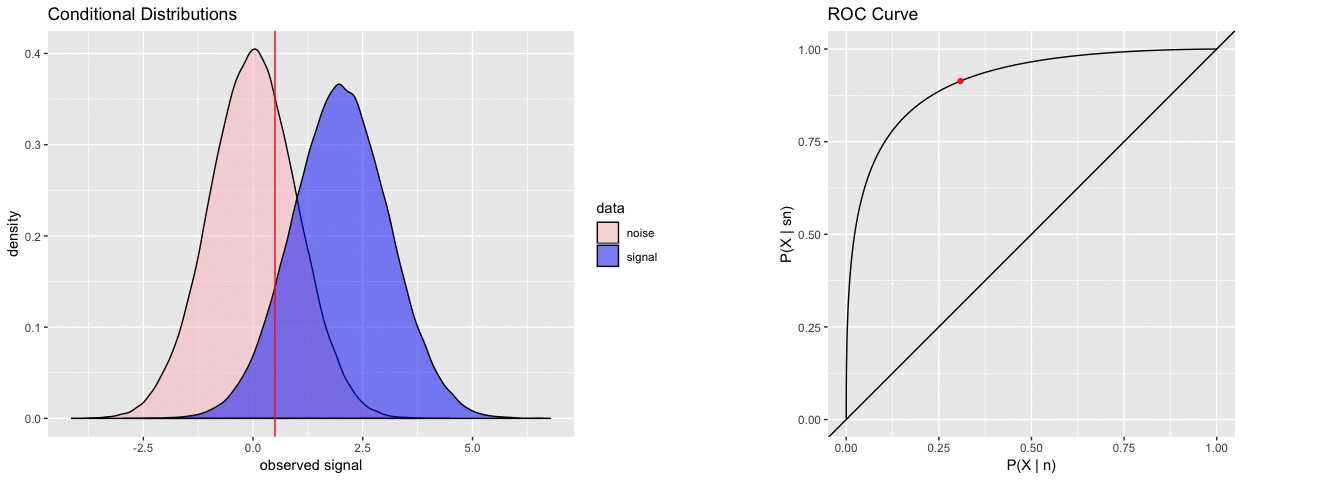
source
ROC曲线中曲线相对于随机线的最高点,表示正例和负例分布的分离程度(一般来说分离程度越大,ROC曲线的“小山包”隆起越明显),“小山包”的面积(ROC曲线和随机线围住的面积)就是Gini指数,如下图所示:
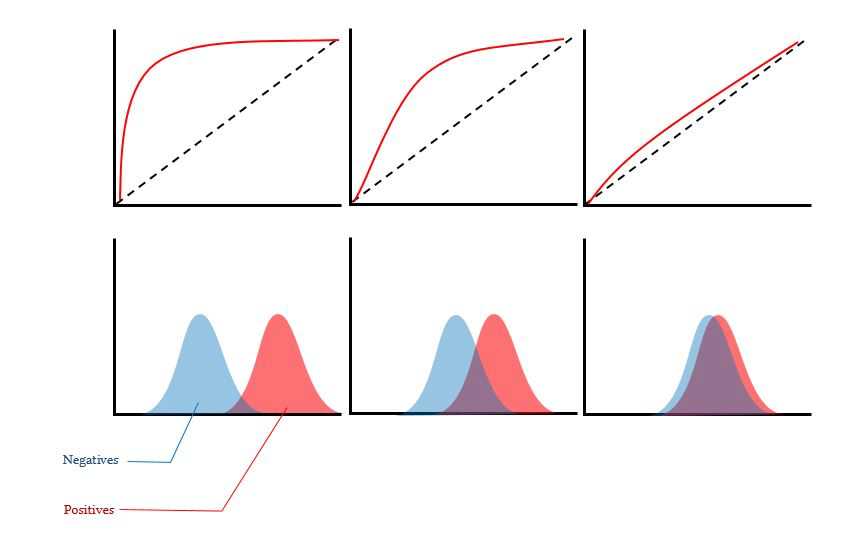
如果模型A的ROC曲线完全包裹模型B的ROC曲线,则表明模型A是优于模型B的;两个模型的ROC曲线发生交叉时,则可以通过ROC曲线下的面积(Area under the ROC curve,简称AUC)来进行比较,AUC取值范围为[0,1].
更多关于ROC曲线的资料:
来源:Cost curves: An improved method for visualizing classifier performance
前面提到的指标都有一个前提,那就是正例或者负例预测错误的代价是一样的(FP,FN)。定义实际为正例预测为负例的损失为\(C(-|+)\),实际为负例预测为正例的损失为\(C(+|-)\).
代价曲线(Cost Curve)中:
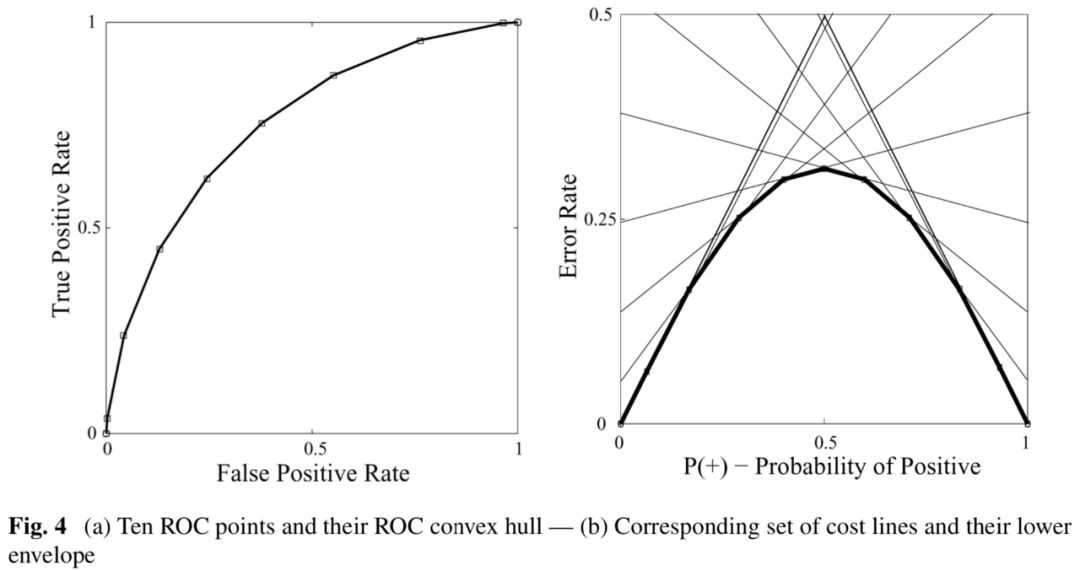
绘制代价曲线时,ROC曲线上每个点的坐标(TPR,FPR)映射到代价曲线上就是一条左起于(0,FPR)到右侧(1,1-TPR)的线段,所有线段绘制好后包裹而成的“小山丘”的面积就是期望的总体代价。
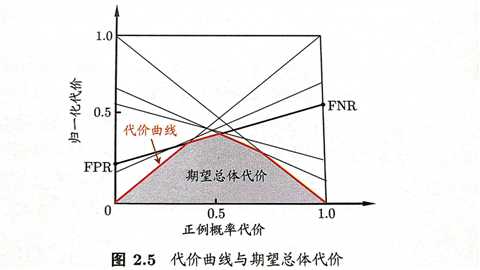
来源:《机器学习》周志华
更多参考:Cost curves: An improved method for visualizing classifier performance, Chris Drummond & Robert C. Holte, 20063.
提升图(Lift Chart,也称为Lift Curve)和收益图(Gain Chart)是从ROC曲线衍生出来的。
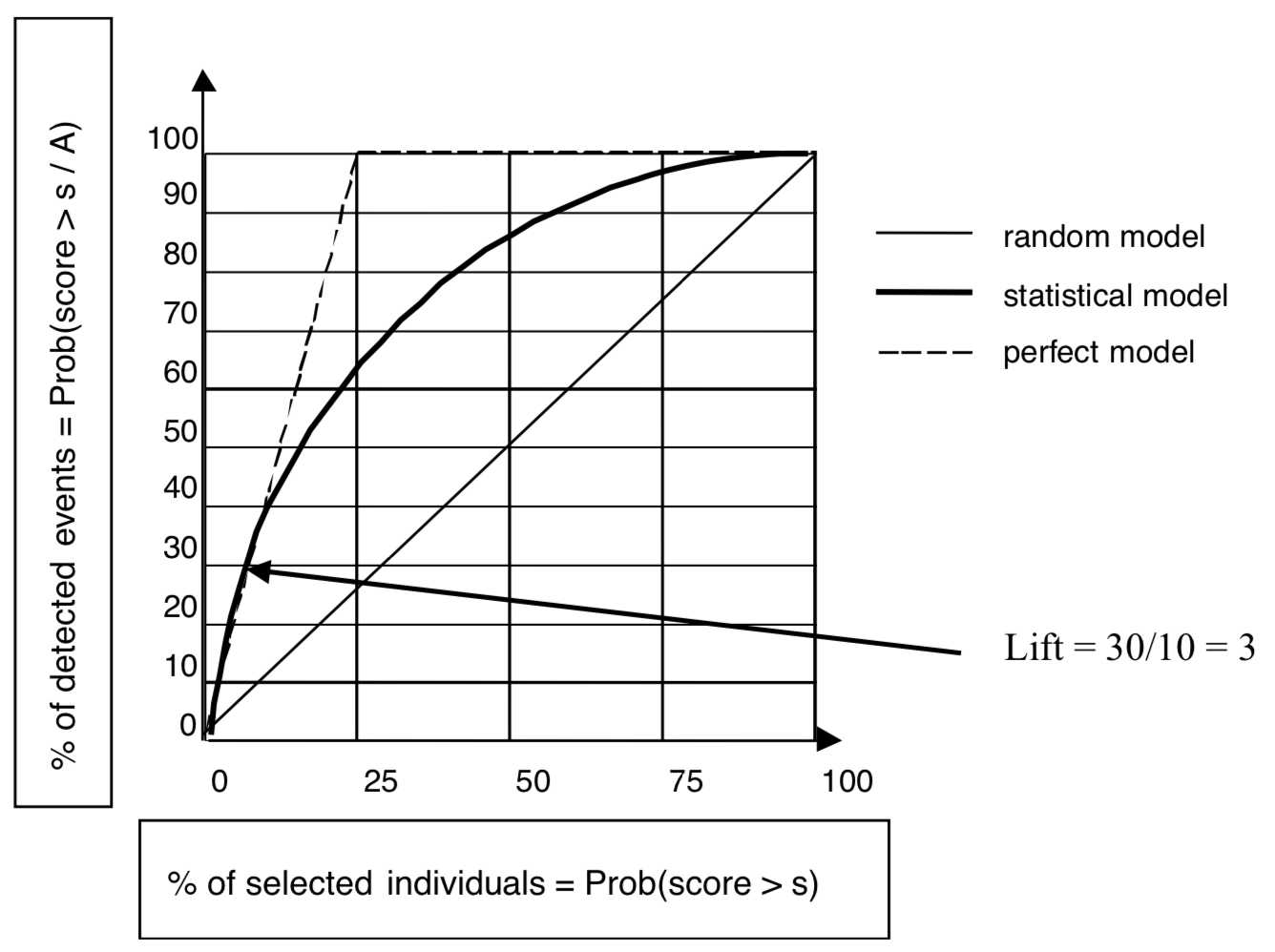
截图来自Data Mining and Statistics for Decision Making , Stéphane Tufféry
Lift公式通过贝叶斯推导可以得到
\[
\begin{aligned}
Lift & = \frac{P(A \bigcap B)}{P(A)*P(B)}\& = \frac{P(A|B)*P(B)}{P(A)*P(B)}=\frac{P(A|B)}{P(A)}\& = \frac{P(B|A)*P(A)}{P(A)*P(B)}=\frac{P(B|A)}{P(B)}\\end{aligned}
\]
公式中的\(P(B)\)可以看做上图中的横轴,也就是每个划分下对应的样本数量占比\(P(p>p_\theta)\)(\(p\)是样本为正例的概率,\(p_\theta\)是正例概率划分点),\(P(A|B)\)就是每个分组中正例的比例\(P(+|p>p_\theta)\).
作Lift曲线时,将样本按预测为正例的概率\(P(+)\)从大到小排序后,按照\(P(+)\)等距划分为N段(取百分位数,一般划分10段),将每1小段当做一个小组,然后计算每个分组中正例的比例,类似如下的表格
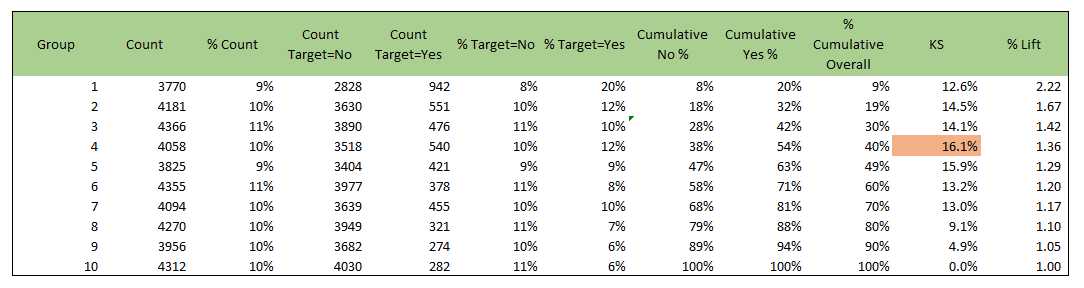
注:表格数据得到的提升图和收益图
更多关于Lift\Gain Curve参考:
更多参考指标可以参考如下cheat sheet

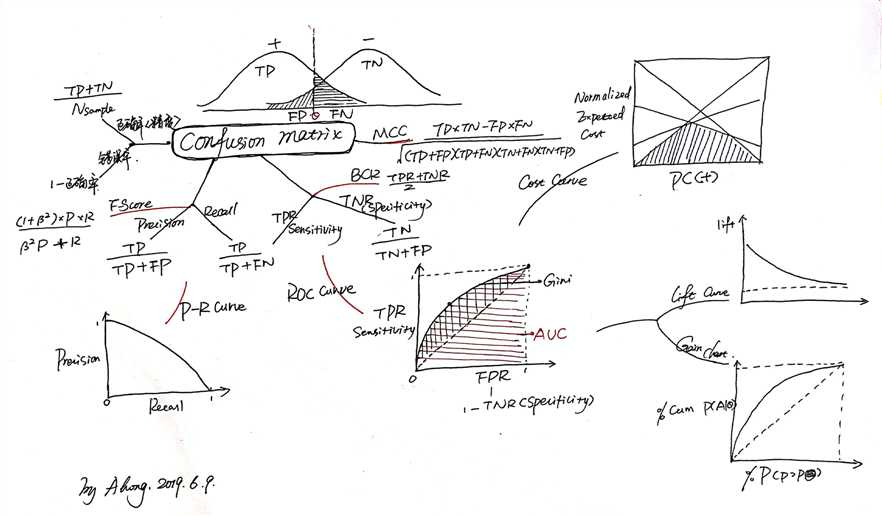
参考资料:
标签:robert 分离 htm att 推导 roc dict ini expect
原文地址:https://www.cnblogs.com/dataxon/p/12538524.html