标签:存在 sam ret factory 完全 细节 递归 模仿 没有
目录
第一单元通过三次迭代的表达式求导任务建立对面向对象程序的初步认识,并熟悉面向对象的思维和编程方法。
三次作业的需求如下:
第一次作业:求解简单多项式导函数
第二次作业:求解包含简单幂函数和简单正余弦函数的表达式的导函数
第三次作业:求解包含简单幂函数和可嵌套因子的正余弦函数的表达式的导函数
从总体上来看,三次任务主要可以分解为以下四个子任务:
从迭代的角度上来看,第一次作业到第二次作业的迭代,只是增加了数据结构的宽度,主要的工作是完成新引入的三角函数因子求导方法以及乘法求导方法的算法建立,对程序架构影响不大,迭代较为简单;第二次作业到第三次作业的迭代由于引入了表达式因子,并且允许因子内嵌套包括表达式因子在内的其他因子,形成了嵌套,且嵌套的深度不可测,改变了数据结构的深度,迭代难度较大,需要进行较大程度的重构。
第一次作业中,只有简单的多项式,简单多项式本质上就是一系列的指数-系数对,且在等价的情况下,可以认为指数是不会重复的,因此能够比较自然地想到表达式Expression内部用map来实现。
第二次作业中,引入了新的简单三角函数因子,因子的多样性使得项的种类不再是线性空间,而成为了由幂函数指数、正弦函数指数和余弦函数指数构成的三维空间,引入了Item类来表示项作为原子结构组成表达式Expression,其本质上是三种函数的指数的组合。
第三次作业中,由于引入了表达式因子且允许嵌套,使得因子的种类也成为了无穷多种,无法再用简单的数构成映射,因此进一步引入Factor类表示因子作为组成Item项的原子,内部引入表达式innerExpr来实现嵌套,并通过Expression.META表示变量元x来实现嵌套的终止。(通过在Factor内部引入Expression进行嵌套主要是因为自己心急提前对第二次作业进行了重构,但在第三次作业下发以后才发现作业要求与自己的设想有部分偏差,这导致了程序的结构其实并不能够很好地适应第三次作业的需求,这也带来了后续对程序进行调整的一些麻烦)。
三次迭代由于需求不断增加,情况变复杂,因此原子数据结构的颗粒度不断减小,最终形成了表达式-项-因子的层次化结构。
下面是三次task的类图:
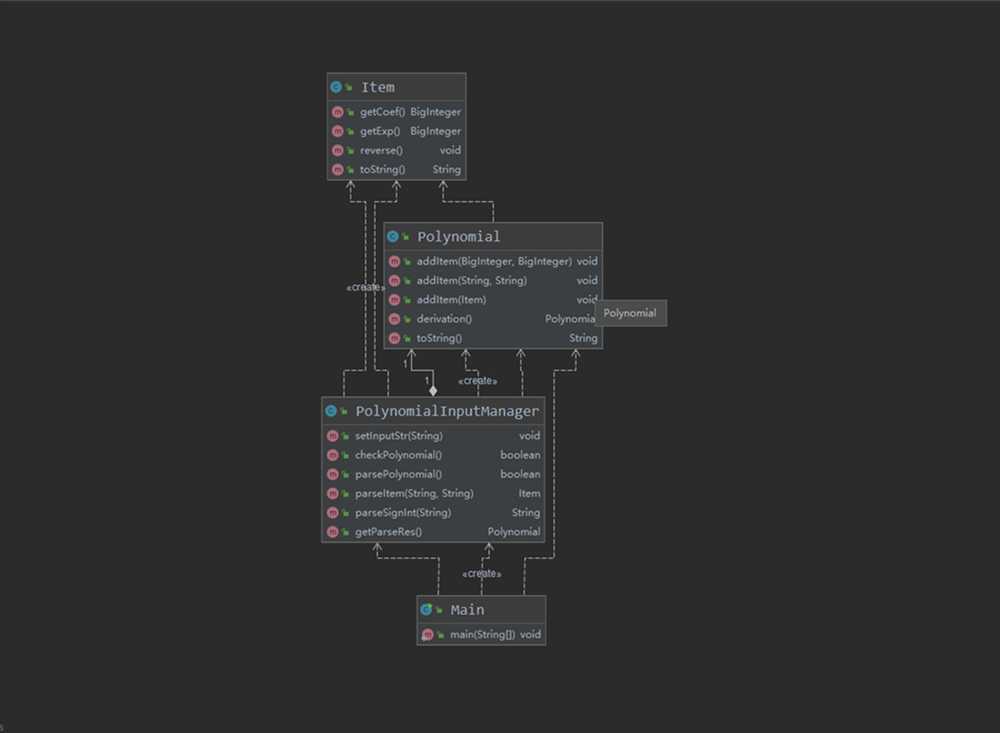
task1
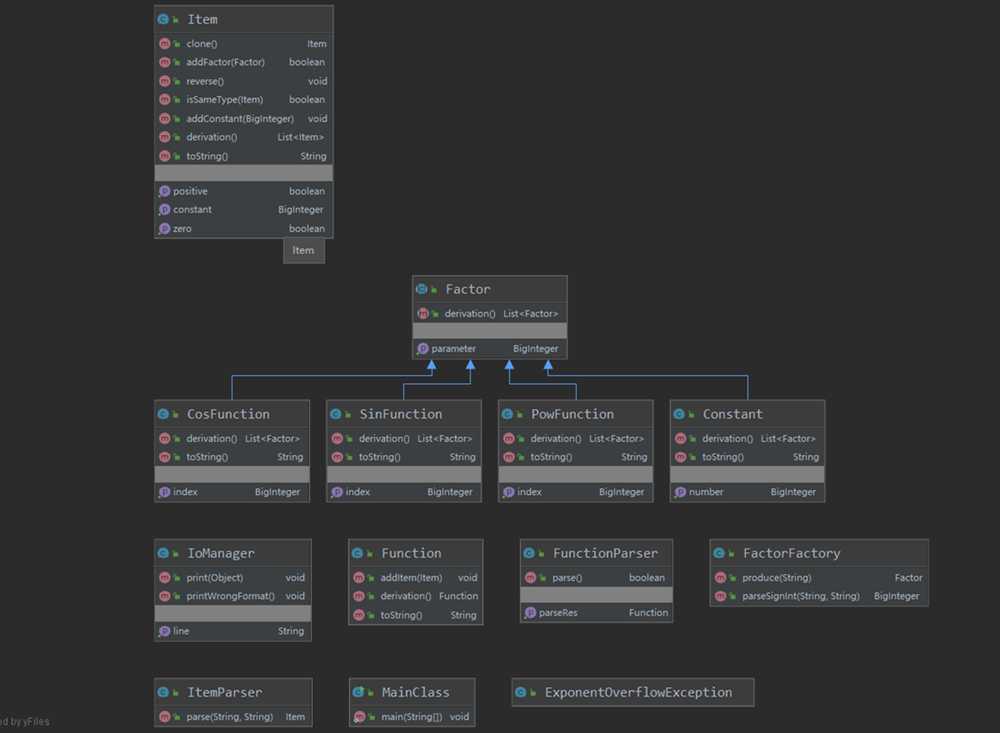
task2
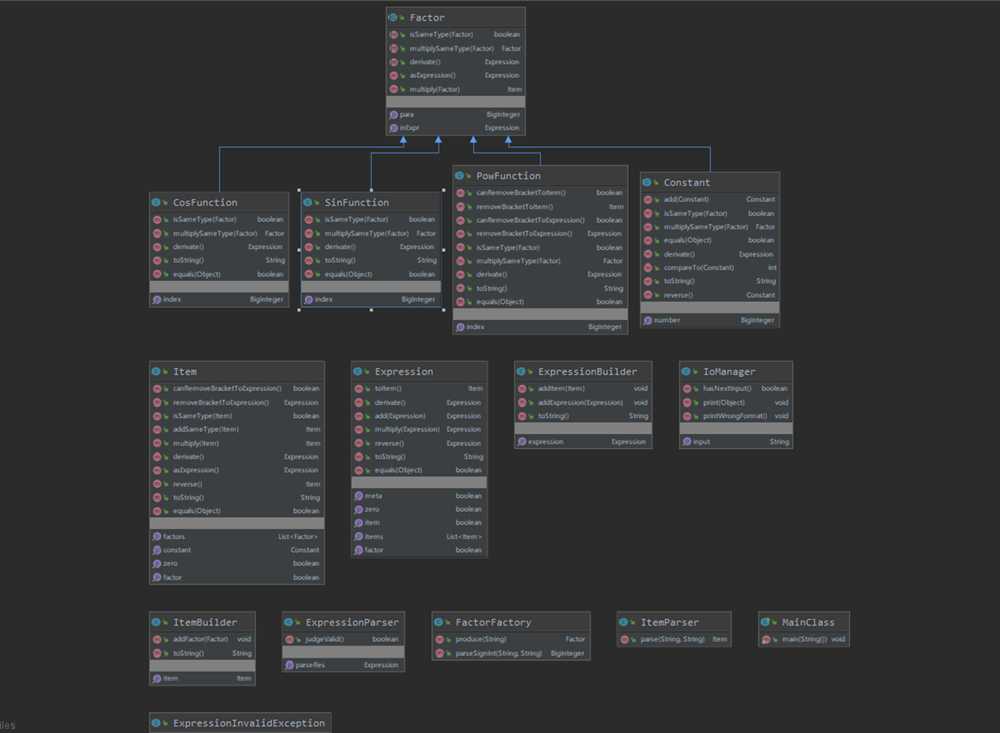
task3
第一次作业,虽然输入的形式比较简单,但是由于对正则表达式不熟悉,所以在输入解析上花费了大量的时间,且代码在长度和结构上都不理想,问题的关键点是自己过于贪心了。最开始的时候,自己希望需求一种方法,用一个大正则匹配整个输入的字符串,在实现格式正确与否的判断,同时提取出所有底层用于建立表达式的信息。一开始的时候这么构思,主要是基于一点考虑,那就是在这个问题中,其实在一个大正则的匹配过程中,所有需要用于构建表达式的信息其实都已经被具体地匹配到了,自己希望能够将这一次匹配的收益最大化。然而经过尝试和查找资料后,发现这种做法存在两个问题:
1. 对于同一个捕获组的多次匹配,在栈中只会保留最后一次捕获的内容;
2. 在同一个模式串中,无法对不同的捕获组取相同的名字,即使逻辑上需要。这就使得我们为了获得不同匹配分支的具体内容(指以`|`所连接的不同模式),需要构建层次化的捕获组命名,引入了不必要的复杂度.由于第1条是硬伤,所以最终不得不妥协,采取了用大正则匹配一次判断格式后,再逐项匹配的方法。由于还是希望充分利用匹配结果,第2个问题依然存在,这使得解析的过程看起来很不优雅,严重影响了程序的可读性。(事后才发现,其实在第一次作业中,第2个是问题是可以避免的,因为所有的项的内容都是最复杂的一种情况的内容的子集)
第二次作业,吸取了第一次作业的教训,采取了层次化解析的方法,具体上来说,通过表达式解析类ExpressionParser先将不同的项提取出来,再将这些项传递给项解析类ItemParser,后者提取出不同的因子传递给因子工厂类FactorFactory产生因子。这样子,虽然增多了实际上不一定需要匹配,但是使得整个表达式的解析层次化,使逻辑清晰。
在第二次作业中,由于表达式的结构还是比较简单,各因子有明显的原子化特征,无论是判格式正确与否还是在不同层次提取信息,采用的都是结合了非匹配组的正则匹配。然而对于第三次作业,由于引入了嵌套,完全使用正则完成解析有很多细节难以控制,其中主要是括号的匹配问题,因此将括号匹配中的栈思想引入了解析过程。
在输入的表达式字符串中,不同的项其实就是由+或-分割的字符串,但是加减作为分隔符是有条件的:
1.不能够出现在某一个括号中
2.不作为项中的符号出现.具体来说,不能项的先导符号,不能是某个带符号整数的符号……对于第一个条件,在遍历输入字符串的时候,引入一个变量stack,初始值为0,当遇到(时自增,当遇到)时自减,当且仅当stack=0的时候遍历到的符号才有可能成为项的分割符;对于第二个条件,经分析后可以知道,只需了解前一个字符的信息即可完成判断。遍历整个字符串,可以找到所有分割项的+和-,根据这些信息将各项再进行分别解析。
对于项的解析,道理是类似的,具体来说分隔符变成了*。
另外,由于嵌套的存在,不可能一开始就用一个大正则判断整个表达式的合法性,只能在层层解析的过程中同时实现判断。这样的情况下,用异常机制处理会较为优雅。
前两次作业,由于结构简单,都直接在项的层次上实现求导的逻辑。
第三次作业由于引入嵌套,需要进行递归。在具体的实现上,依托表达式类Expression的方法multiply()和 add()方法,对各层次对象都实现public Expression derivate()方法,完成求导,并通过常数因子Constant和上面提到的变量元Expression.META来结束递归。
本次采用了边构造边简化的方法,在逐层构建表达式的过程中,通过boolean isSameType(Object o)方法,来判断上层结构的容器中是否含有可以合并的成员,并在判断成功的时候完成相应的合并操作。本次化简考虑的主要是形式化简,并未考虑诸如sin(x)\*\*2+cos(x)\*\*2=1这样子需要考虑数学含义的化简上,有所不足。
| task1 | task2 | task3 | |
|---|---|---|---|
| LOC (lines of code) |
228 | 505 | 1097 |
| ev(G)avg (average essential cyclomatic complexity) |
1.38 | 1.55 | 1.97 |
| iv(G)avg (average design complexity) |
2.52 | 1.96 | 1.81 |
| v(G)avg (average cyclomatic complexity) |
2.71 | 2.20 | 2.54 |
| DIT (depth of inheritant tree) |
1 | 1.46 | 1.40 |
| WMCavg (weighted method complexity) |
12.75 | 8.00 | 16.80 |
| OCavg (Average operation complexity) |
2.43 | 2.04 | 2.36 |
第一次作业的结构性问题主要出在正则解析,前面的部分已经进行了相关的分析;第三次作业在未明确要求的时候进行了重构,导致后续对程序进行调整后程序中某些方法变得臃肿,从而使WMCaveg值较大。
本单元第二次作业中,同一个互测房间的小伙伴们帮助我找到一个bug。在构建表达式向表达式增加项的时候,加入了非零判断,即如果新加入的项为0则不进行添加操作。因此,在重写Item.toString()的时候,没有考虑项为0的情况需要在字符串开头加‘+‘。然而,在合并同类项时也会产生值为0的项,但没有对其进行判断就加入表达式中的容器中了,从而出现了输出错误。
public String toString() {
if (isZero()) {
return "0";
}
StringBuilder res = new StringBuilder();
// The problem is here!
if (isPositive()) {
res.append("+");
}
// ...
}第一次和第三次作业未出现bug。
另外,这次作业找互测房间其他同学的bug主要针对自己编写代码阶段出现的一些觉得比较典型的问题来进行设计。以后要多看其他同学的代码,在有针对性找bug的同时多多学习。
在第二次和第三次作业中,采用了简单工厂方法创建因子Factor对象,工厂类FactorFactory封装了因子种类判断和不同因子的创建过程,通过向其传入一个字符串来直接获取一个对应的Factor对象。
另外,在设计中为了避免可能出现的重复对象引用所带来的潜在风险,将表达式Expression,项Item和因子类Factor都设计为了不可变类型。然而,由于在设计中采用了构建对象过程中进行化简得方式,导致Expression和Item构建的过程较为复杂,不方便直接传参构造。为了解决这个问题,模仿StringBuilder 和String的关系,设计了ExpressionBuilder和ItemBuilder类分别用于Expression和Item的构建。
在自己反思以及与课程组提供的优秀代码进行对比以后,发现了以下几个需要提升的地方:
Expression,Item和Factor类都需要方法Expression derivate()和boolean isSameType(Object o),可以分别创建一个接口并让三个类都实现,从而使程序的逻辑更加清晰。第一单元的学习让我初步认识了面向对象编程的基本方法。很感慨的一点是要想学好一样东西,除了闷着头听好课完成作业以外,自己找到其他的学习途径和拓展的方向是至关重要的。在完成这个单元三次task的过程中,已经引申出了不少可以去进一步学习的点,有从同学们分享中了解到的概念和实用的工具,也有自己在遇到困难时候发掘出的一些暂时没有解决,绕过去了的问题。师傅领进门修行看个人,学习的张力关键看自己。和大家共勉。
最后感谢老师和助教的辛勤付出和大家无私的分享!
标签:存在 sam ret factory 完全 细节 递归 模仿 没有
原文地址:https://www.cnblogs.com/eleony/p/12540182.html