标签:ike 选择 hand for bic das 重复 其他 灵活
参考url:
https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html
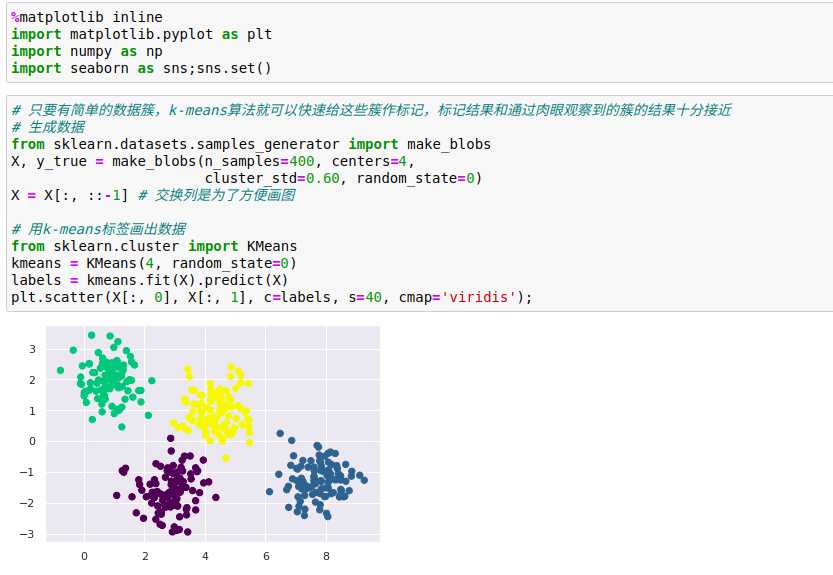
某些点的归属簇比其他点的归属簇更加明确,比如中间的两个簇似乎有一小块区域重合,因此对重合部分的点将被分配到哪个簇不是很有信心,而且k-means模型本身没有度量簇的分配概率或不确定性的方法。
理解k-means模型的一种方法是:它在每个簇的中心放置了一个圆圈(在更高维空间中是一个超空间),圆圈半径根据最远的点与簇中心点的距离算出。这个半径作为训练集分配簇的硬切断(hard cutoff),即在这个圆圈之外的任何点都不是该簇的成员。

k-means有一个重要特征,它要求这些簇的模型必须是圆形:k-means算法没有内置的方法来实现椭圆形的簇,因此,如果对同样的数据进行一些转换,簇的分配就被变得混乱。
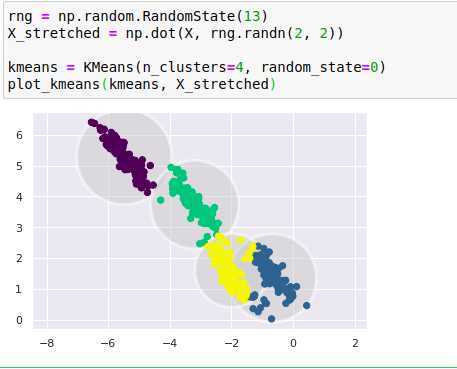
这些变形的簇并不是圆形的,因此圆形的簇拟合效果非常糟糕,k-means强行将数据拟合至4个圆形的簇会导致多个圆形的簇混在一起、互相重叠,右下部分尤其明显。
k-means的两个缺点(类的形状缺少灵活形、缺少簇分配的概率),使得它对许多数据集(特别是低维数据集)的拟合效果不尽人意。
高斯混合模型的两个基本组成部分:
(1)通过比较每个点与所有簇中心点的距离来度量簇分配的不确定性,而不仅仅是关注最近的簇。
(2)通过将簇的边界由圆形放宽至椭圆形,从而得到非圆形的簇。
高斯混合模型(Gaussian mixture model,GMM)试图找到多维高斯概率分布的混合体,从而获得任意数据集最好的模型。
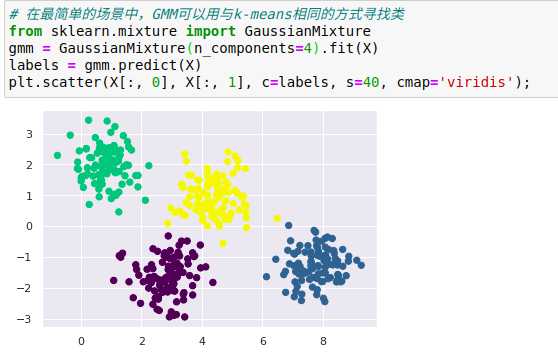
由于GMM有一个隐含的概率模型,因此它也可能找到簇分配的概率结果——在Scikit-Learn中用predict_proba方法实现,这个方法返回一个大小为[n_samples,n_clusters]的矩阵,矩阵会给出任意点属于某个簇的概率。
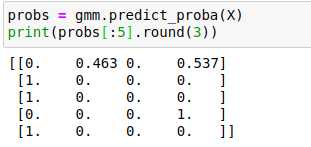
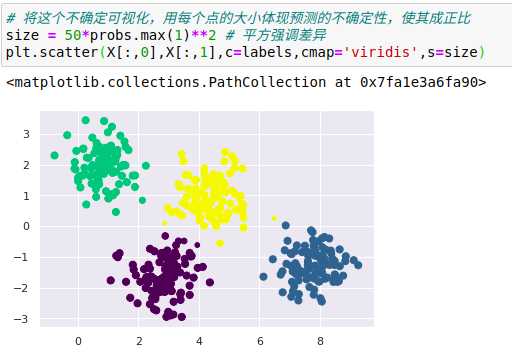
高斯混合模型本质上和k-means模型非常类似,它们都使用了期望最大化方法,具体实现如下:
(1)选择初始簇的中心位置和形状
(2)重复直至收敛
a、期望步骤(E-step):为每个点找到对应每个簇的概率作为权重。
b、最大化步骤(M-step):更新每个簇的位置,将其标准化,并且基于所有数据点的权重来确定形状
每个簇的结果并不与硬边缘的空间(hard-edgedsphere)有关,而是通过高斯平滑模型实现。
高斯模型允许使用全协方差(full covariance),即使是于非常扁平的椭圆形的簇,该模型也可以处理。
其中的超参数covariance_type控制了每个簇的形状自由度,它的默认值是covariance_type=‘diag‘,意思是簇在每个维度的尺寸都可以单独设置,椭圆边界的主轴与坐标轴平行。
当covariance_type=‘spherical‘时,该模型通过约束簇的形状,让所有维度相等,这样得到的聚类结果和k-means聚类的特征是相似的,但两者并不完全相同。
当covariance_type=‘full‘时,该模型允许每个簇在任意方向上用椭圆建模。
虽然GMM通常被归类为聚类算法,但它本质上是一个密度估计算法,从技术的角度考虑,即一个GMM拟合的结果并不是一个聚类模型,而是描述数据分布的生成概率模型。
GMM是一种非常方便的建模方法,可以为数据估计出任意维度的随机分布
作为一种生成模型,GMM提供了一种确定数据集最优成分数量的方法:由于生成模型本身就是数据集的概率分布,因此可以利用该模型来评估数据的似然估计,并利用交叉检验防止过拟合,纠正过拟合的标准分析方法有赤池信息量准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC),用来调整模型的似然估计,这两种度量准则的计算方法内置在Scikit-Learn的GMM评估器内。
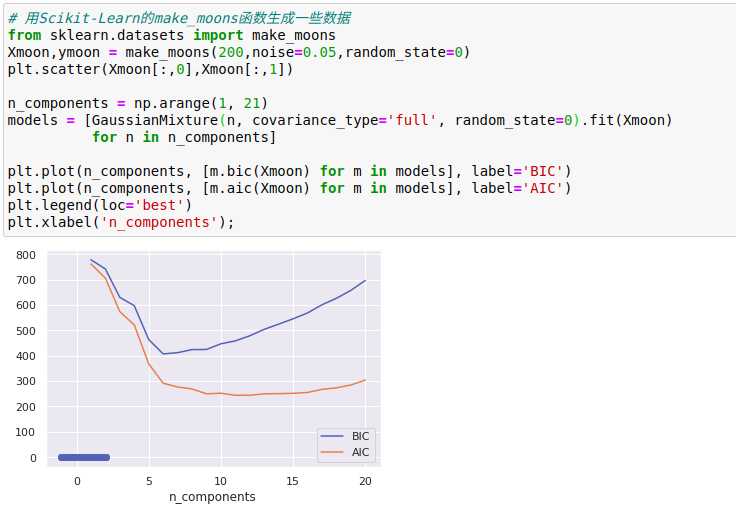
类的最优数量出现在AIC或BIC曲线最小值的位置,最终结果取决于我们更希望使用哪一种近似。
AIC告诉我们,选择16个成分可能太多,8个~12个成分可能是更好的选择。
这里需要注意的是:成分数量的选择度量的是GMM作为一个密度评估器的性能,而不是作为一个聚类算法的性能,建议把GMM当成一个密度评估器,仅在简单数据集中才将它作为聚类算法使用。
标签:ike 选择 hand for bic das 重复 其他 灵活
原文地址:https://www.cnblogs.com/nuochengze/p/12541550.html