标签:朴素 rac pre 数据 优点 最大的 mmm 基础上 形式
哎,最终还是得接受贝叶斯的宠幸。。。==。。
emmm。。
先说之前学的概率公式
如果A, B, C是相互独立的,那么有P(ABC)=P(A)P(B)P(C)。这可推广到n种情况,如果事件A1, A2,?, An是相互独立的,有如下关系(这个公式我们下面会用到,记住哦)
\[P\left(A_{1} A_{2} \cdots A_{n}\right)=P\left(A_{1}\right) P\left(A_{2}\right) \cdots P\left(A_{n}\right)\]
条件概率:
已知事件B发生的情况下,事件A发生的概率记为P(A|B)
贝叶斯算法是有监督学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。
但是有限制条件:
以自变量之间的独立(条件特征独立)性和连续变量的正态性假设为前提,就会导致算法精度在某种程度上受影响
分类的核心就是看属于哪类的概率高
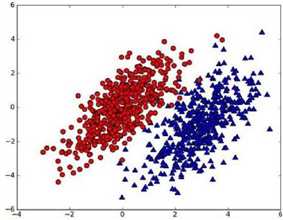
我们现在用\(p_1(x,y)\)表示数据点\((x,y)\)属于类别1(图中红色圆点表示的类别)的概率,用\(p_2(x,y)\)表示数据点\((x,y)\)属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点\((x_0,y_0)\)g,可以用下面的规则来判断它的类别:jack cui
如果\(p_1(x_0,y_0)>p2(x_0,y_0)\),那么类别为1
如果\(p_1(x_0,y_0)<p2(x_0,y_0)\),那么类别为2
我觉得之前的学习没有对全概率公式好好的理解,没关系可以理解了。
可以图和公式相结合嘛
这里有一交集图
\(P(A | B)=\frac{P(A \cap B)}{P(B)}\)
\(P(A \cap B)=P(A | B) P(B)\)
\(P(A \cap B)=P(B | A) P(A)\)
\(P(A | B) P(B)=P(B | A) P(A)\)
\(P(A | B)=\frac{P(B | A) P(A)}{P(B)}\)
参考jack cui
假设A和A‘构成了样本空间S

样本空间中还有一个B
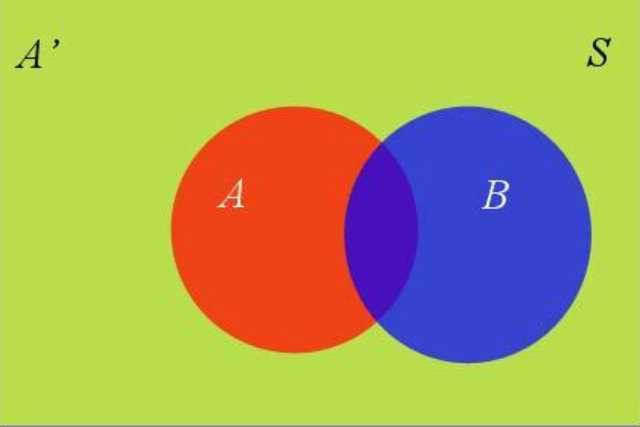
\(P(B)=P(B \cap A)+P\left(B \cap A^{\prime}\right)\)
\(P(B \cap A)=P(B | A) P(A)\)
\(P(B)=P(B | A) P(A)+P\left(B | A^{\prime}\right) P\left(A^{\prime}\right)\)这就是全概率公式
如果A和A‘构成样本空间的一个划分,那么事件B的概率,就等于A和A‘的概率分别乘以B对这两个事件的条件概率之和
于是条件概率的另一种写法
\(P(A | B)=\frac{P(B | A) P(A)}{P(B | A) P(A)+P\left(B | A^{\prime}\right) P\left(A^{\prime}\right)}\)
就是对条件概率的变形,那么怎么来理解
\(P(A | B)=P(A) \frac{P(B | A)}{P(B)}\)
把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。(这里解释的不是很清楚)
后验概率 = 先验概率 x 调整因子
如何理解?
先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。也就是说先测,然后实验进行调整,查看实验之后的效果。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。jack cui
这里抓糖的栗子很形象了
在使用该算法的时候,如果不需要知道具体的类别概率,即上面P(H1|E)=0.6,只需要知道所属类别,即来自一号碗,我们有必要计算P(E)这个全概率吗?要知道我们只需要比较 P(H1|E)和P(H2|E)的大小,找到那个最大的概率就可以。既然如此,两者的分母都是相同的,那我们只需要比较分子即可。即比较P(E|H1)P(H1)和P(E|H2)P(H2)的大小,所以为了减少计算量,全概率公式在实际编程中可以不使用。jack cui
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
朴素贝叶斯推断的一些优点:
生成式模型,通过计算概率来进行分类,可以用来处理多分类问题。
对小规模的数据表现很好,适合多分类任务,适合增量式训练,算法也比较简单。
朴素贝叶斯推断的一些缺点:
对输入数据的表达形式很敏感。
由于朴素贝叶斯的“朴素”特点,所以会带来一些准确率上的损失。
需要计算先验概率,分类决策存在错误率。
晚点补充栗子
标签:朴素 rac pre 数据 优点 最大的 mmm 基础上 形式
原文地址:https://www.cnblogs.com/gaowenxingxing/p/12489871.html