标签:ring 返回 mod 中序遍历 return ack rgs ati new
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
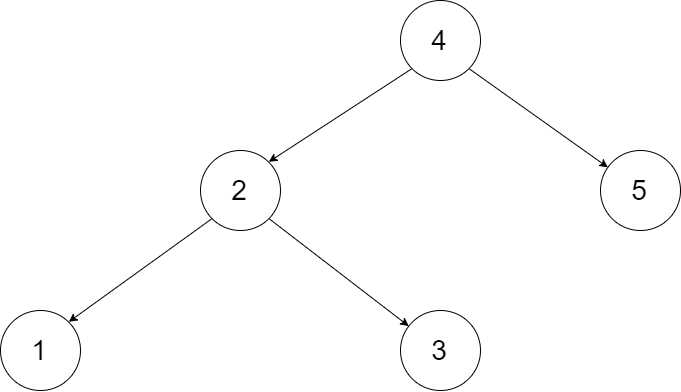
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
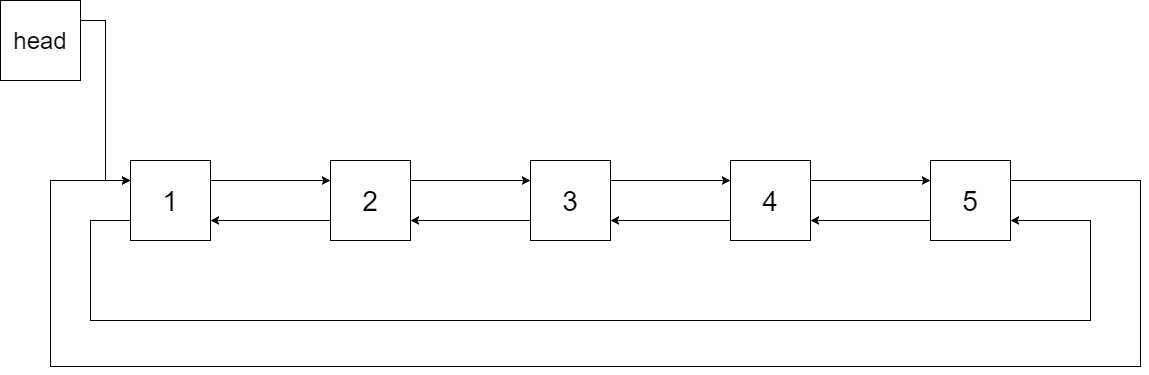
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路:对于二叉排序树而言,其中序遍历输出就是升序排序。那我们怎么将其做成双向链表尼?着手点肯定是中序遍历;在遍历的迭代逻辑中,我们要将前次迭代和本次迭代处理的节点,按照双向链表的要求进行处理。怎么处理尼?通过一个全局变量保存上次遍历的节点,然后再本次遍历的节点处理中进行如下操作:
preNode.right = curNode;
curNode.left = preNode;
当所有节点都这样处理后我们看
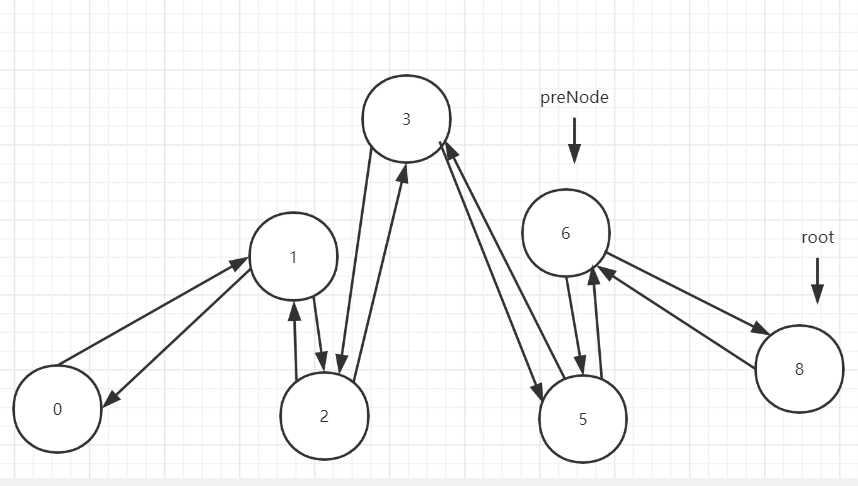
其原本是一个二叉排序树,遍历处理后,root指向尾部,我们这是只需要将head和tail相连就可以构成一个完整的双向链表了。root再处理后就是尾部,然而head我们可以通过循环的方式
Node newHead = root; while(true){ if(newHead.left == null){ break; } newHead = newHead.left; }
一直向左子节点取寻找,直到为null,就到达了最小的节点了,当然也可以再中序遍历中进行操作,因为中序遍历第一个遍历的就是最左子节点,这里把其保存下来就可以了。
这里的递归操作如下:
package JianZhiOffer36; /** * @author :dazhu * @date :Created in 2020/3/23 9:11 * @description: 二叉搜索树与双向链表 * @modified By: * @version: $ */ public class Main { public static void main(String[]args){ } } class Solution { public Node preNode = null; public Node newHead = null; public Node treeToDoublyList(Node root) { //边界条件 if(root == null){ return root; } middleOrder(root); //将处理后的双向链表的首尾相连 newHead.left = preNode; preNode.right = newHead; return newHead; } //算法思路:因为二叉排序树的中序遍历的输出就是有序的列表, //我们改写中序遍历,通过定义一个preNode的全局变量保留当前节点的前一个节点。 //preNode.right = curNode,curNode.left = preNode. public void middleOrder(Node root){ //如果当前节点为null,则return null if(root == null){ return ; } //中序遍历, middleOrder(root.left); //中序遍历,第一个遍历的节点就是最左下的最小节点。 //即第一个访问的节点就为左下角节点。 //如果出preNode,则指向此时root,即为最左下节点。用来第一次遍历时,初始化 //第一次进入这里是最左子节点时,初始化所需节点指引。 if(preNode == null){ newHead = root; preNode = root; }//否则, else{ //以preNode始终指向前一个节点,正好是比当前节点小的节点, //进行以下操作,将其转成双向链表。 preNode.right = root; root.left = preNode; preNode = root; } middleOrder(root.right); } } // Definition for a Node. class Node { public int val; public Node left; public Node right; public Node() {} public Node(int _val) { val = _val; } public Node(int _val,Node _left,Node _right) { val = _val; left = _left; right = _right; } };
标签:ring 返回 mod 中序遍历 return ack rgs ati new
原文地址:https://www.cnblogs.com/dazhu123/p/12552985.html