标签:就是 bsp 定义 而在 一个个 关于 运算符 alt src
就例如一个非常简单的题~
有一堆人 其中某些人是朋友
有如下的规则 如果A和B是朋友 B和C是朋友 那么A和C也是朋友~
最后我们有n次的查询 每次查询问其中两个人是不是朋友?
这个题我们就可以用到集合的思想~
例如A和B是朋友 我们可以把A和B放到一个集合里~
C和D是朋友 我们就把C和D放到一个集合里~
如图
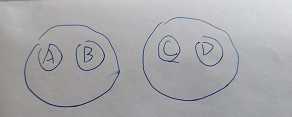
(原谅只会人工画图的笨比)
但如果我们假设A和C也是好朋友
我们就把这两个集合合并起来~

就是这个样子~我们对所有的“朋友对”进行这样的操作 就会把他们分到一个个集合里 这时候查找他们是不是好朋友就很轻松了~
以上这些 就是并查集的思想:
当然我们通过c语言实现并查集也很简单
借助数组!
首先我们定义一个数组!
fa[maxn]
fa代表father的意思 父亲
fa[1]=2就代表1的父亲是2
为什么这么做呢!
因为并查集是一种树状的数组
例如刚才那个例题 我们怎么做才算是把AB,CD分别放到一个集合里呢!
很简单 就是让A的父亲是B,C的父亲是D
fa[A]=B,fa[C]=D
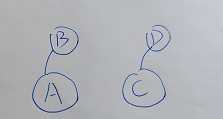
通过这种方式!我们就形象的把A和B连在一起 C和D连在了一起(这样来代表他们是一个集合里的)
之后我们如果知道了A和C是好朋友
我们如何合并(AB)和(CD)这两个集合呢
很简单 我们首先查找A的祖先 然后查找C的祖先
然后让A的祖先 是C的祖先的父亲
fa[A的祖先]=C的祖先
如图:
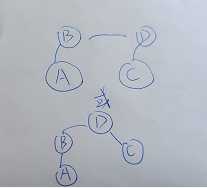
这样一个非常简单的并查集就做好了~
那么我们如何知道查询呢!
就例如查询A和C是不是好朋友
我们首先找A的祖先
A的父亲=B,再找B的父亲=D 所以A的祖先就是D!
那么我们再找C的祖先
C的父亲=D(这时候上面没人了)所以C的祖先就是D!
那么如果A的祖先和C的祖先是一个人!!
如图 就可以证明 A和C在同一个集合中
----------------------------------------------------------------
以上 就是我们一个简单并查集的两大功能
1合并两个集合
2查找
----------------------------------------------------------------
可能这时候你有了一点点小问题
我们该如何知道某个人上面是不是没人了!
(例如上面我们怎么知道C的父亲=D,D就是他的祖先,在上面就没人了呢?)
我们可以在初始化上做操作!
fa[i]=i;
我们初始化上 让每个人的祖先都是他自己!
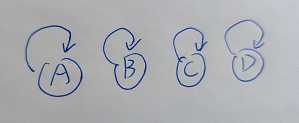
而在上面集合(ABCD)中 我们知道祖先是D D作为最大的 他上面没有其他比他辈大的了
所以按照我们初始化的结果!D的祖先还是D,是他自己
因此 我们只需要找 某个元素的祖先是不是自己 就可以完成祖先的判断
如图: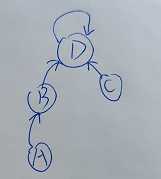
上一波代码实现:
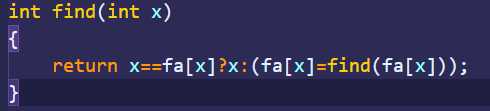
通过三目运算符判断 如果x==x的父亲 那么x就是祖先 如果不是 那么让接着往上寻找父亲的父亲 直到找到一个x=x的父亲的节点 作为祖先
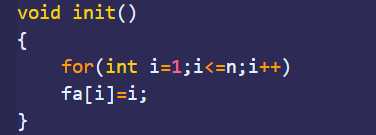
以上为初始化实现(巨简单是不是)
那么如何合并两个集合呢!

也非常简单
首先找到x的祖先 然后找到y的祖先 让(x的祖先)的父亲是(y的祖先)即可!
参考上面例题哦~
以上
就是一个非常简单的并查集啦~
当然还可以进一步的优化等等
今天做题做到了并查集相关的内容~简单介绍一下关于并查集的东西
我是蒟蒻lsr!下期博客见=-=
今天做题做到了并查集相关的内容~简单介绍一下关于并查集的东西
标签:就是 bsp 定义 而在 一个个 关于 运算符 alt src
原文地址:https://www.cnblogs.com/VAthree/p/12555430.html