卡方分布与卡方检验

标签：not   样本   enter   family   val   表数据   比例   出现   span   

卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

它在分类资料统计推断中的应用包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。

举例：

表1 实际统计表格

（一般： 条件2 = ¬条件1 ）通过简单的统计，得出在条件1和条件2下，出现情况1的比例分别为30.94%和25.00%，

两者的差别有可能是误差导致，也有可能是 在条件1下，情况1出现的比例更高。（ 实际假设：在条件1下，情况1出现的比例更高 ，即 条件1 对情况1的出现有影响 ）

为了确定 实际假设 是否成立，先假设 条件1 对情况1 的出现 没有影响，

（ 理论假设： 条件1 对情况1 的出现没有影响 ，理论假设 = ¬实际假设）

在实际统计中，情况1出现的比例为28.29%，那么在理论假设下（即条件1 对情况1 的出现没有影响），表1 条件1和情况1 对应的那一格的数据应该为 139 * 28.29% = 39.3231 。

表1 条件1和情况2 对应的那一格的数据应该为 139 * (1-28.29%) = 99.6769。

同样，表1 条件2 的那几格也按照上面的方式填。

这样得到，理论（条件1 对情况1 的出现没有影响）的表格，如下

表2 理论统计表

如果 理论假设 （条件1 对情况1 的出现没有影响） 成立，那么理论值与实际值的差别应该会很小。

理论值与实际值的差别的计算就会用到卡方公式：

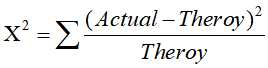
将 表1 和 表2 对应格的数据带入公式得到 卡方值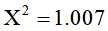

接下来是利用这个 卡方值 ，通过查 卡方分布的临界表 ，来判断 理论假设（条件1 对情况1 的出现没有影响）是否成立。

这里需要用到一个自由度的概念，自由度等于F = (行数 - 1) * (列数 - 1)，对四格表，自由度F = 1。

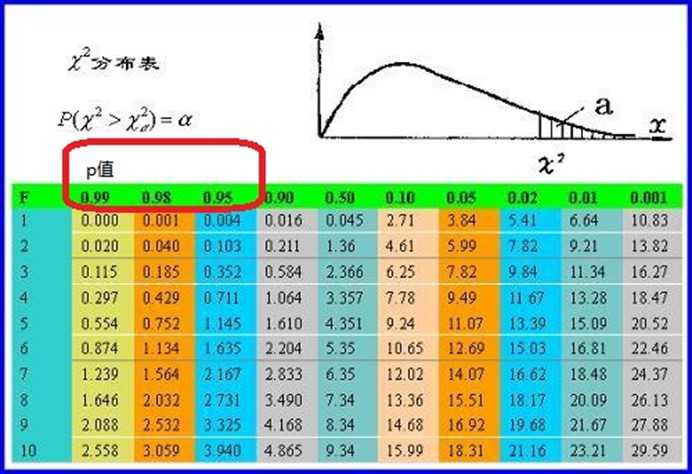
图1 卡方分布表

查图中的表数据第一行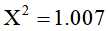， 在0.045 和2.71 之间，对应的 P值在 0.1 到 0.5 之间，

说明 实际假设 跟 理论假设 的差别很 小（以 理论假设 为基础），只有0.5（1-0.5）到 0.9 （1-0.1）之间的把握可以接受 实际假设 成立，那么即 理论假设 成立。

相反，实际假设 跟 理论假设 的差别很 大（以 理论假设 为基础），P值越小，有越大的把握接受 实际假设 成立。

卡方分布与卡方检验

标签：not   样本   enter   family   val   表数据   比例   出现   span   

原文地址：https://www.cnblogs.com/lincz/p/12562621.html