标签:1的个数 回文 mic event alt lan eve 两种 std
给你两个数$n, m$代表有$n$个偶数,$m$个奇数。让你输出$n$个偶数$m$个奇数从中任选两个数(没有顺序)相加结果为偶数的个数。
相加为偶数只有偶加偶和奇加奇两种情况,其实就是在$n$个数中取两个($C\binom{2}{n}$),在$m$个数中取两个($C\binom{2}{m}$)。
时间复杂度$O(1)$

1 #include <iostream> 2 using namespace std; 3 int main() { 4 long long n, m; 5 cin >> n >> m; 6 cout << n * (n - 1) / 2 + m * (m - 1) / 2; 7 return 0; 8 }
定义一个字符串 $S$ 是强回文串当且仅当 $S$,$S_{1...\frac{(|s|+1)}{2}}$ 和 $S_{|s|-\frac{(|s|+3)}{2}+1...|s|}$都是回文的。判断一个回文串是不是强回文串。$3 \leq |s| \leq 99$且$|s|$是奇数。
直接取出每一部分的字符串,判断到中心距离相等的位置的字符是否相等即可。
时间复杂度$O(|s|)$。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 char s[100], tmp[100]; 6 int top; 7 int n, nn; 8 int main() { 9 scanf("%s", s + 1); 10 n = strlen(s + 1); 11 nn = n; 12 for (int i = 1; i <= nn; i++) { 13 if (s[i] != s[nn - i + 1]) { 14 puts("No"); 15 return 0; 16 } 17 } 18 nn = (n - 1) / 2; 19 for (int i = 1; i <= nn; i++) { 20 if (s[i] != s[nn - i + 1]) { 21 puts("No"); 22 return 0; 23 } 24 } 25 nn = (n + 3) / 2; 26 for (int i = nn; i <= n; i++) { 27 tmp[++top] = s[i]; 28 } 29 for (int i = 1; i <= top; i++) { 30 if (tmp[i] != tmp[top - i + 1]) { 31 puts("No"); 32 return 0; 33 } 34 } 35 puts("Yes"); 36 return 0; 37 }
给定一个整数x。求所有各棱长为实数且和为x的长方体中最大的体积是多少。
小学奥数题...
和一定差小积大。
其实就是一个均值不等式。
设棱长为$a,b,c$,则 $a \times b \times c \leq \frac{(a+b+c)^3}{27}=\frac{x^3}{27}$,当$a=b=c$时成立。

1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 double l; 5 int main() { 6 scanf("%lf", &l); 7 l = l / 3; 8 printf("%.12lf", l * l * l); 9 return 0; 10 }
我们有n个数,每个数都在[1,n]中,如果去掉第k个数,问剩下的数有多少对相同的数(不计顺序),$1 \leq n \leq 2 \times 10^5$。
我们可以把n个数中有多少相同的数对,因为每个数都很小所以这点我们可以用堆来做。
设cnt[i]代表i这个数出现的次数所以答案等于$\sum_{i=1}^{n}\frac{cnt[i] \times (cnt[i]-1)}{2}$。
现在我们来看删掉一个值为x的数。
cnt[x]的值减小了一,它的贡献变成了$\frac{(cnt[x]-1) \times (cnt[x]-2)}{2}$,相比之前减少了cnt[x]-1。
设不删时的答案是tot,则删掉一个权值为x的数的答案为tot-(cnt[x]-1)。
单词询问复杂度O(1)。

1 //这里sum就是cnt 2 #include <iostream> 3 #include <cstdio> 4 using namespace std; 5 const int N = 2e5 + 10; 6 int n, a[N]; 7 long long sum[N], tot; 8 int main() { 9 scanf("%d", &n); 10 for (int i = 1; i <= n; i++) scanf("%d", &a[i]), sum[a[i]]++; 11 for (int i = 1; i <= n; i++) { 12 tot += sum[i] * (sum[i] - 1) / 2; 13 } 14 for (int i = 1; i <= n; i++) { 15 printf("%lld\n", tot - (sum[a[i]] - 1)); 16 } 17 return 0; 18 }
我太弱了,我比赛时这题竟然都没调出来。
有一个$n \times m$的矩阵,每个位置要不是要不不是零,用尽量少的次数把这个矩阵切成几块(只能把整行或整列与下一行或列切开,具体可看下面的例子)使得每一块中1的个数少于某个常数。
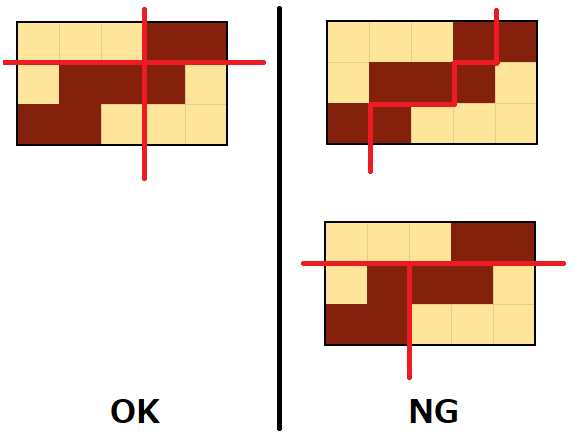
$1 \leq n \leq 10, 1 \leq m \leq 1000$
我们发现n非常的小,于是我们可以枚举行之间且的情况,再判断列之间要切的情况,取最小值即可。
时间复杂度$O(2^n \times n \times m)$
【ATcoder】AtCoder Beginner Contest 159题解
标签:1的个数 回文 mic event alt lan eve 两种 std
原文地址:https://www.cnblogs.com/zcr-blog/p/12550421.html